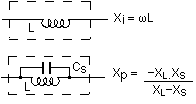Producing wound components

This page provides practical guidance for students, staff and researchers at this University who need to wind their own inductors, transformers or solenoids. The types of wound components available, and their applications, are so varied that only general guidelines can be provided. A more complete appreciation of their capabilities (and limitations) is only gained through experience and experimentation.

Before deciding to produce a custom inductor consider whether you have an alternative. If you are designing a filter circuit, for example, then below about 100kHz it becomes attractive to use either op-amp circuits or switched capacitor ICs instead. If an inductor has to be used then look to see if it can be obtained as an 'off the shelf' part from one of the usual distributors.

Here is a procedure that you can follow to design an inductor. It may not be the quickest way (it's somewhat 'trial and error') but it's easy to follow and understand -

Decide what type of core is best.
Calculate how many turns to put on.
Check that saturation will not occur.
Decide what type of wire to use.
Check that there is enough space to hold the wire.
Obtain the parts.
Construct the coil.
Test the coil.

If you find at step 5 that the core size selected in step 1 cannot accommodate the number of turns of the wire chosen then select a larger one and start again at 2.

See also ...
[ Up sign ESU Advisor index] [Using the ESU coil winder] [ Air coils] [A guide to the terminology used in the science of magnetism] [ Power loss in wound components] [The force produced by a magnetic field] [ Faraday's law] [Bibliography] [Acknowledgements]

Choosing a Core

The most important considerations in core selection are usually -

Inductance value
Whether the inductance must be adjustable
Frequency coverage (Fmax)
Maximum current (Imax)
Permissable losses.

A very approximate guide might be -

Appropriate core types
Min H	Max H	Type of Core	Adjus- table?	High current?	Frequency limit
20 nano Henry	1 micro Henry	Air cored, self supporting	Y	Y	1GHz
20 nano Henry	100 micro Henry	Air cored, on former	N	Y	500MHz
100 nano Henry	1 milli Henry	'Slug' tuned open winding	Y	N	500MHz
10 micro Henry	20 milli Henry	Ferrite ring	N	N	500MHz
20 micro Henry	0.3 Henry	RM Ferrite Core	Y	N	1MHz
50 micro Henry	1 Henry	EC or ETD Ferrite Core	N	Y	1MHz
1 Henry	50 Henry	Iron	N	Y	10kHz

Ring cores

Ring cores (AKA 'toroids') are compact, inexpensive and useful when relatively few turns are needed. Without special apparatus they are rather tedious to wind and the current handling is limited because no air gap is possible. For these reasons they are mainly used above 100 kHz.

Rings may be supplied with a coating of polyamide, polyurethane or other insulation. This helps to reduce self-capacitance by keeping the turns away from the ferrite (some grades have relative permittivities approaching 10⁶).

Rings made from iron dust are also available. These can have saturation points of 1T or more but permeabilities of 30 or less are common for dust cores. Some grades will perform well into the VHF region. Magnetic field leakage is low.

RM cores

RM cores are a popular choice at frequencies up to 1MHz and currents up to 1A. The formers are supplied with up to 8 pins which bring connections to or from the coil(s) and which may easily be incorporated into a PCB layout. The bobbin material is brittle and care must be taken not to bend the pins. The clips holding the core at the sides are pretty crude and it's easy to chip the ferrite when removing them. For these reasons I do not recommend them for prototype work.

Two basic types of RM cores are available: gapped and ungapped. Ungapped cores suitable for power applications are available with a different grade of ferrite which has a lower permeability but a higher value of saturation flux.

The size designations, RM6, RM7, RM10 etc. indicate that adjacent cores require a minimum spacing of 0.6, 0.7 or 1.0 inches on the PCB.

E Cores

EC and ETD cores are intended for high power applications such as switch mode power supplies and DC to DC converters. For experimental work I recommend the ETD29 core in preference to the RM core because it has more space and the pins are more numerous and robust. Transfer your design to the RM if you decide that a smaller 'footprint' is needed.

If using an ungapped EC core you can place thin pieces of plastic between each half to obtain a gap which can be made precisely the right width.

Slug Tuned Coils

There are currently three types of slug tuned coil assemblies in use in the School. These have 6 PCB pins and are suitable for low power IF transformers, filters and tuned circuits. They are most suitable when the inductance required must be adjustable. See separate description of these cores.

[ Up sign Top of page]

Iron Cores

Iron is the oldest magnetic core material. Its advantages include a high saturation flux (2.1T) and a high relative permeability (7000). It is no longer used for transformers in its pure form for two reasons.

Firstly, iron has high remnance (1.3 T) and coercivity (80 A m^-1). This results in hysteresis power loss. The remedy is to include a small (about 3%) amount of silicon. This reduces the loss by at least a factor of 10.

Secondly, iron will conduct current. This is bad in a transformer core because eddy currents lead to further power loss. As a result transformers with iron cores are limited to audio frequencies or below. Even then, the iron is used in stacks of thin sheets (laminations).

[ Up sign Top of page]

Calculating the number of turns

Decide the number of turns to wind on according to what you want to achieve: a known inductance, winding current or winding voltage waveform ...

Known inductance

For ferromagnetic core inductors this is simple if you know the value of inductance required and the quoted A_l value of the core.

N = (10⁹ × L / A_l)^1/2

Example: We need to make an inductor using the standard example toroid core. How many turns do we need for 82 μH?

N = (10⁹ × 82×10^-6 / 2200)^1/2 = 6.1 turns

If the coil is air cored then you will need to re-arrange one of the traditional formulae for calculating the inductance of such coils from the dimensions and the number of turns.

Known winding current

A common strategy is to work the core at close to its saturation flux level.

N = B_sat×l_e/(µ×I) turns

Example: We need to make an inductor capable of carrying 1.3 amps using the standard example toroid. How many turns can be used?

N = 0.36 × 27.6×10^-3 / (1.257×10^-6 × 2490 × 1.3) = 2.4 turns

In other words, we cannot put on more than two turns without hitting saturation! This gives us just 8.8 nH. Makes yer fink.

Known winding voltage waveform

The maximum total core flux is given by:

= B_sat×A_e

By re-arranging Faraday's law,

N = ( E.dt ) / turns
where E is the externally applied voltage.

Example: We need to make a transformer for a switching supply using the standard example toroid. The supply to the primary is 12 volts and the maximum 'on time' for the switch is 10 micro seconds. How many turns must we use?

= 0.36×19.4×10^-6 = 6.98×10^-6 webers

N = (12×10^-5)/(6.98×10^-6) = 17.2 turns

Here we must round up to 18 turns. With the current driven winding the flux increased with the number of turns but with a voltage driven winding the flux goes down with the number of turns. Honest. Please address any complaints on this issue to m.faraday@ri.ac.uk.

[ Up sign Top of page]

Choosing the type of wire

In almost all cases this will be single strand 'enamel' insulated, also known as magnet wire. The coating is usually of poly vinyl acetal, polyester or polyurethane. The last of these is self-fluxing during soldering. It is manufactured to tightly controlled specifications laid down in standards such as BS 4520 and NEMA MW*. It can stand temperatures up to 120 centigrade or more for long periods.

There are some possible exceptions to this choice -

Coils carrying currents above about 3A. If you are using a small diameter core (RM series) it can be difficult to manipulate thick enamel wires. A better idea is to divide the winding up into two or more thinner wires which are wound on simultaneously and joined at the ends. An additional advantage of this approach is that losses due to skin effect are reduced.

Low loss coils with a Q-factor higher than about 200 and 'Wave wound' coils having a high self resonant frequency. For these coils it may be necessary to employ multi-strand 'Litz' wire. Wave wound coils cannot be produced using wire with standard enamel insulation on the outside because the turns slide over each other too easily (a product called Gripeze does have a non-skid surface). Cotton covered wires are sometimes used.

The next step is to calculate the thickness of wire required.

For self supporting coils this is usually decided on mechanical grounds; the larger the diameter of the coil the larger the diameter of wire used. A coil of 6 millimetre internal diameter might use 0.5 millimetre wire. Increase this pro rata if the coil takes heavy current.

For normal coils the diameter is chosen so that temperature rise and efficiency are both acceptable. Modern insulation materials are able to withstand temperatures so high that designing for t_max alone is probably not sensible. See the section on copper losses for more details.

You are encouraged to bring your own supplies of wire if using the Workshop winding machines but if the quantity you require is small (<20g) then ask a member of Workshop staff.

Handling wire

Always handle reels of thin enamel wire by the ends. When such wire is used in equipment at high temperature or high voltage for long periods of time then the acids present in fingerprints can lead to insulation failure.

After using a reel please anchor the ends of the wire to the bobbin either using tape or by a hole or slot cut in the flange. Never simply tuck one turn under another; the next user won't realise what has happened and will attempt to unwind the free end - until the reel jams, usually leaving it a write-off.

[ Up sign Top of page]

Coil formers

Coil formers, which are made of an insulating material, are bobbins onto which wire may be wound so that each turn is of the correct diameter and is held in place around whatever core material (if any) is used.

If you need many turns (>20) and wish to use one of the coil winders in the workshop then you must use a coil former.

[ Up sign Top of page]

Self resonance

Self resonance is the term used to describe the way in which the electrical characteristics of wound inductors deviate at high frequencies from that of an ideal inductor. The reactance of an ideal inductor increases linearly with frequency.

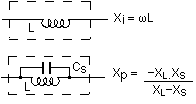
Ideal and practical models

The practical inductor model includes a capacitor in parallel with the ideal inductor in order to represent stray capacitance between each turn and the turn next to it. There will also be distributed capacitance to any core that is used, and an exact model is too difficult to derive.

The consequence of this stray capacitance is that at some point (called the self resonant frequency) the impedance of the inductor will reach a peak. At higher frequencies the stray capacitance will become dominant and the impedance will begin to drop.

If you are deliberately using the inductor as part of a resonant circuit then it is important to note that the Q factor of a self resonant circuit is generally not high. Better values of Q can be obtained by choosing a smaller value of L and adding external capacitance to tune it. This behaviour is the reverse of that predicted by the simple formula for Q.

[ Up sign Top of page]

Saturation

Saturation is a problem which may occur in an inductor having a ferromagnetic core. Initially, as current is increased the flux increases in proportion to it. At some point, however, further increases in current lead to progressively smaller increases in flux. Eventually, the core can make no further contribution to flux growth and any increase thereafter is limited to that provided by the permeability of free space (µ₀) - perhaps three orders of magnitude smaller. Ferrites will normally saturate between about 200mT and 500mT.

It is usually essential to avoid reaching saturation since it is accompanied by a drop in inductance. In many circuits the rate at which current in the coil increases is inversely proprtional to inductance (I = V * T / L). Any drop in inductance therefore causes the current to rise faster, increasing the field strength and so the core is driven even further into saturation.

Core manufacturers normally specify the saturation flux density for the particular material used. You can also measure saturation using a simple circuit. There are two methods by which you can calculate flux if you know the number of turns and either -

The current, the length of the magnetic path and the B/H characteristics of the material.
The voltage waveform on a winding and the cross sectional area of the core - see Faraday's Law.

Although saturation is mostly a risk in high power circuits it is still a possibility in 'small signal' applications having many turns on an ungapped core and a DC bias (such as the collector current of a transistor).

If you find that saturation is likely then you might -

Use a larger core
Use a core with an air gap.

[ Up sign Top of page]

Air gaps

Problems with saturation can be reduced by using a core with an air gap. Some cores are manufactured with a built in gap; usually of about 1millimetre length. It is often possible, particularly with EC cores, to introduce a gap using a spacer consisting of a small sheet of paper or thin plastic. Whatever the technique, the result is a reduction in the effective permeability of the core, µ_e.
Since B = µ₀ × µ_e × H the flux density can then be decreased below the saturation level.

You might object that this will also lead to a reduction in inductance which can only be compensated for by increasing the number of turns. With more turns the magneto-motive force will increase which will lead to higher flux once more. This argument is only partially correct because inductance increases according to the square of the number of turns whereas mmf is linearly proportional to N. Looked at another way, what you are doing is to shift the burden away from the core and onto the copper wire - after all, an air cored inductor can never saturate.

An analysis of the core and gap as a two component series circuit gives

µ_e = µ_r / (1 + (µ_r × l_g / l_e))

Where l_g is the length of the gap. If you use a spacer then l_g will be twice the spacer thickness because flux must cross the spacer twice in a complete circuit of the core.

The advantages of an air gap can be summarised

Higher values of mmf can be tolerated before saturation takes place
Reduced core losses (higher 'Q' factor).
The inductance is less temperature sensitive.
Cores can be obtained in adjustable versions.

The disadvantages of the air gap are -

More turns are required to obtain a given inductance.
Increased losses in the windings (lower 'Q' factor).
Increased leakage inductance.
Increased radiated field.
Increased succeptability to external fields.

The most serious of these is usually leakage. Values as high as 20% are seen in practice (particularly if a spacer has been used for the gap) and this can have a disasterous effect upon the efficiency of switching supplies. Those using the 'flyback' principle with gapped transformers are especially vulnerable to leakage effects.

[ Up sign Top of page]

Calculating the space for the windings

Once the thickness of wire and the number of turns has been decided, a check should be made that sufficient space exists on the coil former. It is sometimes imagined that turns can be packed in thus -

Naive packing scheme

This is impossible because if the first layer is wound from the left hand side of the coil former to the right hand side and has a normal 'right handed thread' (like a screw) then the second layer will have a 'left handed thread' as it moves back from the right side to the left. Since the turns on adjacent layers do not lie precisely parallel to one another, and must cross over at some point, they cannot always sit in the arrangement shown above. That said, the 'hop over' stretches may be quite short and much of the turn may still be in close contact with the turns below.

In practice you should allow for each layer to be separated by the whole thickness of the wire from the one underneath. The value of thickness used should be taken about 10% greater than the actual thickness to allow for irregularities. This applies only where the wire is fed on taking care that one turn is in close contact with the next. When thin wire (<0.2 millimetres) is used then this becomes impractical. About 15% should be added to the real diameter in the case of 'random wound' coils.

The wire sizes quoted in catalogues always refer to the diameter of the conductor. The enamel insulation increases this by about 10%.

Example -

  Core type RM7,  conductor diameter 0.56 millimetres


  From data sheet -
    Length of winding space = 7 millimetres
    Height of winding space = 3.1 millimetres

  Nominal diameter including insulation = 0.56 × 1.10 = 0.62
  Working diameter of wire = 0.62 × 1.10 = 0.68 millimetres

  Turns per layer = 7 / 0.68 = 10
  Maximum number of layers = 3.1 / 0.68 = 4

  Total = 10 × 4 = 40 turns.

This method produces conservative estimates which allow for any lead-out wires and extra insulation that may be needed.

Usually it is only possible to keep close packing going for about 4 or 5 layers without the 'cross over' effect mentioned spoiling the winding. By placing a layer of polyester or masking tape round the coil after every 2 or 3 layers to 'stabilise' the winding then close packing can be continued indefinitely.

[ Up sign Top of page]

Sources of Supply

Not all companies are prepared to deal in the small quantities that an experimenter usually requires. Try to reward those that are with a sensibly sized order.

Wire. Synthetic enamel insulated wire between 0.2 millimetres and 1.5 mm diameter comes from RS Components Ltd.. A range of iron and ferrite transformer kits is available as well as tapes and adhesives suitable for use on windings.
Other sizes of wire and also Litz try

The Scientific Wire Co.
18, Raven Road
London E18 1HW
Tel. 0208 5050002
General. A large list of manufacturers and distributers is maintained by the International Coil Winding Association.

Here are a few external links which may be of use to you:

Coil manufacturers:
Coilcraft
Core manufacturers:
Amidon inductive components
EPCOS (formerly Siemens)
Fair-rite
Ferroxcube (formerly Philips)
Neosid
Telcon
Winder manufacturers:
ACE Winders
Ingrid West
Other sources of information:
Trade organisation for copper
International Coil Winding Association

[ Up sign Top of page]

Constructing the coil

There are two basic types of enamel wire insulation. You will need to remove it at the ends to make electrical connection.

1) Conventional enamel. This is usually dark brown in colour. In a production environment it is removed by a special rotary stripping machine. For prototype construction thick (>0.2mm) wire is best stripped with a scalpel blade. Rest the wire on a firm, flat surface and scrape the blade along at right angles to the wire.

Thinner wire is best stripped with fine sandpaper or emery cloth, although this is very slow. The process can be speeded up by first burning the enamel using a fine gas jet. This will leave a carbonized residue but this is much easier to sand away.

2) Self-fluxing enamel. This is usually pink or straw coloured. If you have a solder pot then simply dip the end of the wire in for a few seconds. The enamel will melt readily leaving you with a ready tinned end.

You can also remove the insulation if you have a soldering iron hot enough to melt it - about 400 centigrade. Most thermostatically controlled irons can be adjusted to run at this temperature. The joint will have been made correctly after the insulation is seen to 'bubble' for a second or two. When this happens the fumes emitted contain a small quantity of toluene di-isocyanate gas which is toxic and irritant. Use adequate ventilation. If this does not happen then the iron is not at the right temperature. Provided the soldering temperature is adequate, 'dry' joints are very rare.

[ Up sign Top of page]

Testing the coil

Any of the digital readout inductance bridges should give a reasonably good idea of the inductance of your coil. More precise tests can be made with the HP bridge in the final year lab. This can test over a range of frequencies, and can also determine the Q factor.

If you don't get the right inductance then remember that this is related to the square of the number of turns. If your inductance is 20% too low then you must increase the turns by just under 10%.

If you are building a power transformer then bear in mind the non-linearity of permeability.

[ Up sign Top of page]

Dead Tree

Most of these publications are out of print but I've included them as sources of reference.

Agilent Technologies, 'High Accuracy and Fast RF Inductor Testing', Applicaton Note 369-10.
Do precisely what it says in the title ... if you have a HP 4285A LCR Meter.
Balanis, Constantine A. 'Antenna Theory', 2nd. Edit., John Wiley, 1997, ISBN 0-471-59268-4
Heavily mathematical but unavoidable if you are into loop antennas. SI units.
Babani, Bernard B. 'Coil Design and Construction Manual', Bernard Babani (publishing) Ltd. 1960, ISBN 0 85934 050 3
Empirical formulae, data tables and construction guidance. Highly practical. Mainly iron-core devices; no ferrites. Non-SI units.
Flanagan, William M. 'Handbook of Transformer Design & Applications', 2nd. Edit., McGraw Hill, ISBN 0-07-021291-0.
Written by someone with much experience of the design and specification of power transformers. Strong on materials selection and reliability criteria. Non-SI units.
Grover, Frederick W. 'Inductance Calculations (Working Formulas and Tables)', Instrument Society of America, 1946, ISBN 0-87664-513-9.
A very comprehensive collection: Mutual and self inductance for all geometries of air coil, the force between coils. Non-SI units.
Hammond, P. and Sykulski, J.K., 'Engineering electromagnetism: physical processes and computation', Oxford University press, 1994, ISBN 0 19 856288 8.
The most accessible introduction to electromagnetic field theory that I have seen. Bundled with DOS software for numerical analysis. SI units.
Jansson, L. E. 'Power-handling capability of ferrite transformers and chokes for switched-mode power supplies', Technical Note 31, Mullard Limited, 1975.
All you need to know in order to determine the power throughput of a given core in any switching configuration.
Kaye, G.W.C & Laby, T.H. 'Tables of Physical and Chemical Constants', 14th. Edit., Longman, 1973, ISBN 0 582 46326 2.
A useful source of data for scientists, but only about 8 pages relate to the magnetic properties of materials. SI units.
Kraus, John D., 'Electromagnetics', 4th. Edit., McGraw-Hill, 1991, ISBN 0-07-112661-9.
A deservedly popular text, many illustrations, covers a lot of ground. Magnetic components are described in preparation for Maxwell's equations and finally antennas. Rationalised SI units (tables included).
Nadkarni, M.A., S.R.Bhat 'Pulse Transformers, Design and Fabrication', McGraw-Hill 1985.
Has a practical approach. Non-SI units.
Smith, Ralph J. 'Circuits Devices and Systems', 2nd. Edit., John Wiley. 1971, ISBN 0-471-80170-4
A general electronics textbook from my day (i.e. now out of date). About 100 pages within Part III relate to the material here. Lots of helpful examples. MKS units.
Snelling, E.C. 'Soft Ferrites Properties and Applications', 2nd. Edit., Butterworths, ISBN 0-408-02760-6.
If you are using a ferrite core and this book doesn't have the answer then you are in trouble. Wide ranging both in theory and practice. The maths is intelligible and (bliss o' joy) uses SI units. I can't afford a copy of my own :-(
Terman, F.E. 'Radio Engineers' Handbook', McGraw-Hill 1943.
An influential work which, together with 'Radio Engineering', supplied the practising engineer with information previously buried in scientific papers and technical journals. Early editions are strong on air coils, skin effect, mutual-inductance, self-capacitance and Q-factor. Mixture of cgs and Imperial Units.
Wheeler, H.A. 'Simple Inductance Formulas for Radio Coils', Proc. I.R.E., Vol 16, p.1398, Oct.1928

There is a longer list of references at http://www.mag-inc.com/techlit.html.

[ Up sign Top of page]

Acknowledgements

Thanks go to the following for their assistance on the subject wound components:

Mr. Chris Johnston - Typo eradication.
Mr. Kenneth Kirk, Waukesha Electric - Pedagogical polish.
Mr. Mike Leeming, Pima Community College - Linearity of µ.
Mr. Ram Murthy, Siemens Passive Components - Core supplies.
Mr. Geoffrey Russell-Price - Donation of winding wire.
Mr. R A Raichur - Metrication of skin depth calculations.
Mr. Roland West, Ingrid West Machinery - Winder supplies.

[ Up sign Top of page]

E-mail: R.Clarke@surrey.ac.uk
Last revised: 2001 May 26th.