The force produced by a magnetic field

You're designing an electromagnet, for example, and need to calculate the number of turns, or you might already have a coil and want to know how hard it will pull on a nearby piece of iron. These are simple questions. Although the answers are elusive this page outlines some general principles and pointers towards specific solutions.

The energy in a magnetic field.
Uniform magnetic fields
A simple experiment with a solenoid.

About your browser: parts of this page will not render correctly at present (particularly pre IE5 or NS6). if the character in brackets here [ × ] does not look like a multiplication sign then try setting your browser to use the Unicode character set (view:character set menu on Netscape 4).

See also ...
[ Up sign Producing wound components] [ Air coils] [A guide to the terminology used in the science of magnetism] [ Power loss in wound components] [ Faraday's law]

The energy in a magnetic field

One method of calculating the force produced by a magnetic field involves an understanding of the way in which the energy represented by the field changes. To derive an expression for the field energy we'll look at the behaviour of the field within a simple toroidal inductor. We equate the field energy to the electrical energy needed to establish the coil current.

When the coil current increases so does the magnetic field strength, H. That, in turn, leads to an increase in magnetic flux, greek letter phi . The increase in flux induces a voltage in the coil. It's the power needed to push the current into the coil against this voltage which we now calculate.

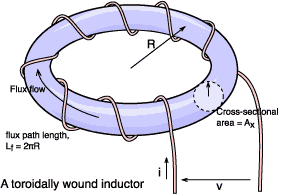Ideal toroid inductor We choose a toroid because over its cross-sectional area, A, the flux density should be approximately uniform (particularly if the core radius is large compared with it's cross section). We let the flux path length around the core be equal to L_f and the cross-sectional area be equal to A_x. We assume that the core is initially unmagnetized and that the electrical energy (W) supplied to the coil will all be converted to magnetic field energy in the core (we ignore eddy currents).

W = time integral v×i dt joules

Faraday's law gives the voltage as

v = N×d/dt volts

Substituting:

W = integral N(d/dt)i dt

W = flux integral N×i d

Now, N×i = F_m and H = F_m/L_f so N×i = H×L_f. Substituting:

W = flux integral H×L_f d

Also, from the definition of flux density greek letter phi

= A_x× B so d

= A_x×dB. Substituting:

W = dens integral H×L_f×A_x dB joules

This gives the total energy in the core. If we wish to find the energy density then we divide by the volume of the core material:

W_d = ( dens integral H×L_f×A_x dB)/(L_f×A_x)

W_d = H dB joules m^-3 Equation EFH

If the magnetization curve is linear (that is we pretend B against H is a straight line, not a curve) then there is a further simplification. Substituting H = B/µ

W_d = dens integral B/µ dB

W_d = B²/(2µ) joules m^-3 Equation EFB

Compare this result with the better known formula for the energy stored by a given inductance, L:

W_L = L×I²/2 joules

Another squared term, you notice.

[ Up sign Top of page]

Uniform magnetic fields

A 'hand-waving' explanation might help clarify the physics. Take an initially uniform magnetic field in free space and introduce into it an iron sphere. The flux lines will bend in the vicinity of the iron so that they will converge upon it. Inside the iron the lines will be quite concentrated (though parallel to the original field).

Now, the point is that there will be no net force on the iron, no matter how strong the field. A sphere has perfect symmetry, so rotation will not change the picture in any way. If there is translational movement then all that can happen if the sphere were to move is that the distortion of the field around the original position of the sphere will disappear and the same distortion will be re-established around the new new position; the total system energy will remain unchanged.

OK, instead of the sphere let's try an iron rod. This is different because we've lost symmetry. What happens is that the axis of the rod will be drawn into alignment with the field - like a compass needle. The flux lines prefer the iron to the air because of the higher permeability. Equation EFB has µ on the denominator so the field energy is lower here than in the air, and the further the flux can go through the iron the lower the energy. Think of current flow through a resistor; the current has an easier time going through a low resistance than a high resistance. Flux goes easier through high permeability than through low. When the rod is aligned with the field the flux can go further through a high permeability region. Note that we still don't have a translational force (provided that the field is uniform on the scale of the rod). Think about the famous experiment with iron filings sprinkled onto a piece of cardboard above a bar magnet. The filings tend to line up with the field but don't generally move much because they are so small that the field appears uniform to them.

So for there to be a force on a piece of iron then a displacement of the iron must result in an alteration to the field energy. The electromagnet you are using will have an opinion about changes to the field it generates. It will say that its inductance is changing. This is the basis of one solution to the problem:

F = (I²/2)dL/dx newtons Equation EFS

where I is the coil current and x is displacement in metres. This result is proved in textbooks such as Hammond, and also Smith. Unfortunately, it might be tricky to calculate how the inductance changes unless the system you have is particularly simple to analyze. You might need computer software such as described by Hammond in order to do it.

[ Up sign Top of page]

A simple experiment with a solenoid

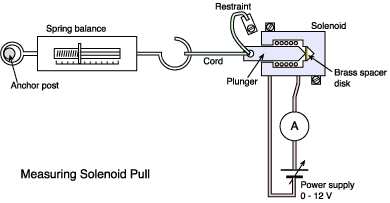A 'solenoid' is the term used to describe the type of electromagnet supplied with an iron piston or plunger pulled in by the field generated by current in a coil. Experimental arrangement to measure
solenoid pull.

Experimental arrangement to measure
solenoid pull.

Solenoids are frequently used to operate valves, release locks or operate ratchets and so on. Equation EFS above suggests that the pull of a solenoid should be related to the square of the coil current. Take a medium sized 12 volt solenoid (having a plunger about 13 mm diameter) and test this out by attaching it to a spring balance as shown in the figure here. Measurements are made as folllows:

Set a high coil current by turning the power supply up towards 12 volts.
Push the plunger in until it is retained by the field.
Reduce the length of the cord until either the balance reads maximum load or the solenoid just retains the plunger. A turnbuckle is handy here.
Make a note of the force measured by the balance.
Reduce the current slowly, keeping an eye on the meter reading, until the solenoid lets go, and note the current. The restraining cord is essential unless you want to be hit in the eye by a lump of iron moving at very high speed :-)

Repeat the sequence, slackening the cord on the balance each time to obtain a lower force. This gave the line, shown below, which has a slope of about 1.1.
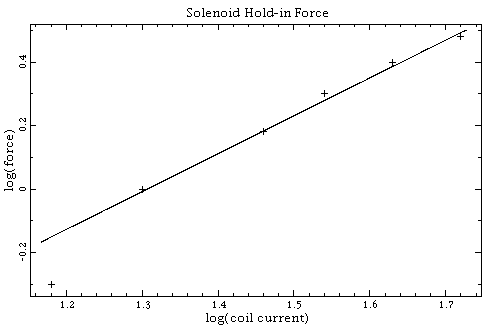
Graph of force v current - no gap

Hmmm ... what may be happening is that non-linearities in the permeability of the iron are affecting the field. If I add a 2 mm thick piece of brass on the end of the plunger then I get:
Graph of force v current - with gap

Notice that the retaining force is now much lower even though a higher coil current has been used. Well, this line has a slope of about 2.2 - a bit closer to theory. In an air gap the flux density is exactly proportional to field strength (and thus current). As far as a static magnetic field is concerned brass behaves just the same as air: the permeabilty is a steady µ₀ at any value of B.

It would be nice to extend this experiment by a measurement of coil inductance against force in order to test Equation EFS. The difficulty is that inductance meters use AC test signals. Without laminated iron (which is only found in solenoids designed for AC operation) the reading will be affected by large eddy current losses.

[ Up sign Top of page]

E-mail: R.Clarke@surrey.ac.uk
Last revised: 2001 March 11th.