Energy Loss

  A particle passing through matter interacts with electrons and with nuclei, possibly also with the medium as a whole (Cherenkov radiation, coherent bremsstrahlung). A light projectile colliding with a heavy target particle will be deflected ( Multiple Scattering), but will lose little energy unless the collision is inelastic

(see Bremsstrahlung, Pair Production). A heavy projectile colliding with a light target will lose energy without being appreciably deflected.

The average energy loss of a hadron is mainly due to strong interactions, which eventually even destroy the particle ( Calorimeter). Nevertheless, electromagnetic energy loss of hadrons is important, because the mean free path for strong interactions ( Collision Length) is large.

Except when the projectile is highly relativistic, ionization is the main electromagnetic contribution to the energy loss. The mean energy loss (the stopping power) due to ionization is given by the Bethe-Bloch formula [Barnett96], for more discussion [Leo94]).

with

where

E = projectile energy

M = projectile mass

= projectile velocity (in units of c) =

z = projectile charge (in units of elementary charge)

x = path length

D =

= 2.817 938 10^-13 cm = classical electron radius

= 0.511 003 MeV/c² = electron rest mass

= 6.022 10²³/mole = Avogadro's number

Z = atomic number of the medium

A = atomic weight of the medium [g/mole]

= mass density of the medium [g/cm³]

I = average ionization potential

= density correction

C = shell correction

= higher order correction.

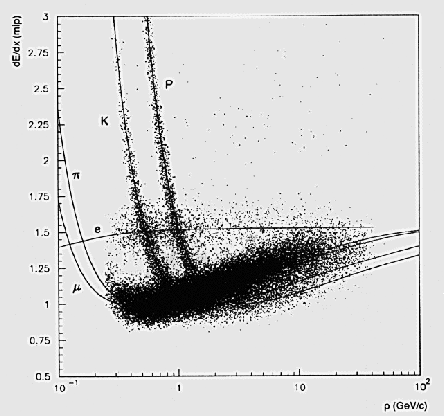
The ionization energy loss is to a good approximation proportional to the electron density in the medium (given by ) and to the square of the projectile charge, and otherwise depends mainly on the projectile velocity. It decreases with for increasing velocity until reaching a minimum around = 3 to 4 (minimum ionization ), then starts to rise logarithmically (relativistic rise ) levelling off finally at a constant value (the Fermi plateau ). The numerical value of the minimum ionization (more precisely: of minimum energy loss) is  MeVcm²/g.

The first expressions for energy loss are due to Bethe and Livingston, later Rossi gave more refined descriptions including various correction terms (see [Rossi65], [Livingston37]).

Sternheimer has worked in detail on the density effect which is at the origin of the Fermi plateau [Sternheimer71]. For a complete review, see [Fano63].

The formulae and in particular the corrections include absorber-dependent terms defying simple description (e.g. ionization potential and shell correction). Hence energy loss is usually given in graphical or tabular form ( e.g. [Barnett96]). Extensive tables for the energy loss of p, K, and in many materials have been computed by Richard and Serre ([Serre67], [Richard71]), where the Bethe-Bloch formula is also discussed with respect to the units used.

Measurements of energy loss, when giving enough care to calibration problems, can be used to identify particles if a simultaneous measurement of momentum is available. For details, Ionization Sampling and Ionization Sampling and [Allison91]. An example for measurements is the following diagram, obtained in a time projection chamber, taken from [Abreu96]:

The ionization energy loss is statistically distributed around its mean value. The distribution, often referred to as energy straggling , is approximately Gaussian for thick absorbers, but develops asymmetry and a tail towards high energies for decreasing thickness; it becomes a Landau distribution for very thin absorbers ( [Leo94] or [Matthews81]).