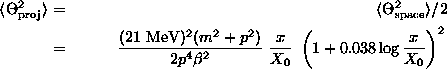
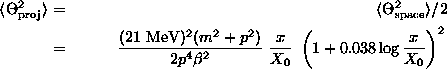
where
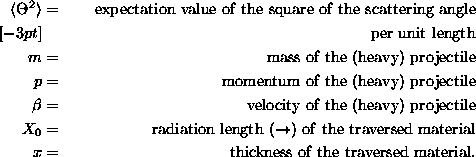
The underlying assumption of a Gaussian distribution makes this approximation a crude one; in particular, large angles are underestimated by the Gaussian form. For more details see [Rossi65], [Scott63], [Fernow86], [Barnett96].
In the general case, the scattering effect, considered as white noise, is described by
with s = path length, 
= influence of the scattering angle 
at s on the impact point C in detector k, and 
=
white noise.
For a straight track in a homogeneous medium and with detectors perpendicular to the track 
, y(0)=0, 
, it follows that
and with (writing 
for 
)
:
and similarly
or written as a matrix
Up to quadratic properties this is equivalent to the Gaussian probability density function
The effects of multiple scattering on track reconstruction were first described by Gluckstern [Gluckstern63]. In track fitting a matrix formalism for multiple scattering can be used. To the (usually diagonal) covariance matrix describing the detector resolution a non-diagonal term taking into account multiple scattering must be added:
where 
is a random variable describing the change of the ith measurement due to multiple scattering for particles travelling parallel to the x-axis and detectors normal to this axis, and E stands for expectation value.
For discrete scatterers (obstacles) and particles moving parallel to the x-axis and detectors normal to this axis, this covariance matrix is given by
The sum is over all obstacles with 
.
A detailed discussion of this matrix formalism is given in [Eichinger81].