Understanding VCO Concepts
OSCILLATOR FUNDAMENTALS
An oscillator circuit can be modeled as shown in Figure 1 as the combination of an amplifier with gain
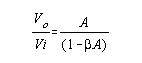
which states that the system will oscillate, provided
Although the model shown in Figure 1 can be used to analyze and determine the necessary and sufficient conditions for oscillation, it is easier to use the model shown in Figure 2 where the analysis is performed in terms of a negative resistance concept. This is based on the concept that a tuned circuit, once excited, will oscillate continuously if there is no resistive element present to dissipate the energy. It is the function of the amplifier to generate the negative resistance or maintain oscillation by supplying an amount of energy equal to that dissipated. The selection of the circuit topology is dictated by several factors:
(a) Frequency of oscillation
(b) Tuning range
(c) Choice of transistor, and
(d) Type of resonator.
Figure 1
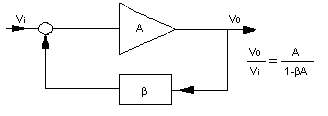
An oscillator may be modeled as the combination of an amplifier and a feedback loop
Figure 2

An oscillator may be modeled using a negative resistance concept
EXAMPLES OF OSCILLATOR DESIGN
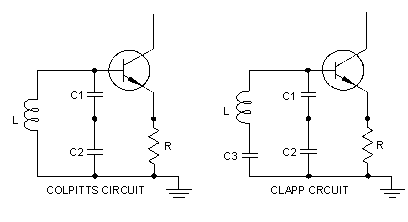
A bipolar transistor with capacitances between the base and emitter, and the emitter and ground, can be used to generate a negative resistance. Examples of these circuits are shown in Figure 3.
Figure 3
Form of oscillator circuit discussed (RF equivalent)
An inductive resonator may be used in any parallel resonant oscillator circuit such as Colpitts or Clapp. The resonator operates at a point where it resonates with the load capacitance. The circuit of Figure 3 is preferred for high stability oscillator circuits because of the ease with which the resonator may be isolated from the load.
Consider the circuit shown in Figure 4(a). The design equations are derived below by replacing the circuit by its equivalent circuit. This is illustrated in Figure 4(b).
The input impedance seen to the right of the dotted line in Figure 4(b) is given by
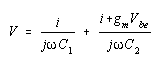
where 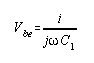
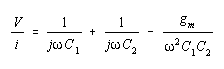
The quantity (gm/2 C1.C2) is negative indicating a negative resistance component and therefore in
order to maintain oscillations we must have
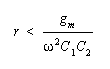
where r is the series resistance of the resonator.
The frequency of oscillation is given by
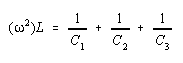
The ratio C1/C2 is selected to be greater than 1 so that the circuit has sufficient loop gain for start
up condition at the lowest operating temperature. A VCO is obtained by replacing a fixed
capacitor such as C3 with a varactor. The bipolar transistor with an inductive reactance between
the base and the ground can also generate a negative resistance (See Figure 5). This topology is
preferred at higher frequencies. The oscillator is obtained by adding a tank circuit as shown in
Figure 6.
Figure 4(a) and 4(b)
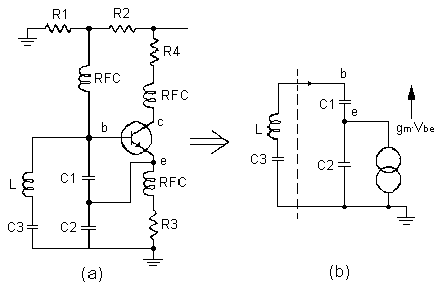
Oscillator design evaluation for CLAPP circuit
Figure 5

Common base circuit configured for generating negative resistance
Figure 6

Common base circuit configured as an oscillator
TUNING SENSITIVITY CHARACTERISTICS
There are two basic types of varactors: Abrupt and Hyperabrupt. The abrupt tuning diodes will provide a very high Q and will also operate over a very wide tuning voltage range (0 to 60 V). The abrupt tuning diode provides the best phase noise performance because of its high quality factor.
The hyperabrupt tuning diodes, because of their linear voltage vs. capacitance characteristic, will provide a much more linear tuning characteristic than the abrupt diodes. These are the best choice for wide band tuning VCO's. An octave tuning range can be covered in less than 20 V tuning range. Their disadvantage is that they have a much lower Q and therefore provide a phase noise characteristic higher than that provided by the abrupt diodes.
For a varactor diode, the capacitance is related to the bias voltage by the following equation:
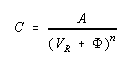 ............(1)
............(1)
where A is a constant, VR is the applied reverse bias voltage, and ![]() is the built-in potential
which is 0.7 for silicon diodes, and 1.2 V for Gallium Arsenide diodes. For the analysis that
follows, we may write
is the built-in potential
which is 0.7 for silicon diodes, and 1.2 V for Gallium Arsenide diodes. For the analysis that
follows, we may write
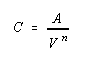 ............(2)
............(2)
where A is the capacitance of the diode when V is one volt and n is a number between 0.3 and
0.6, but can be as high as two for an abrupt junction. The tank circuit of a typical VCO has a
parallel tuned circuit consisting of an inductance L, a fixed capacitance Cf, and a varactor diode
C. The frequency of oscillation can be written as
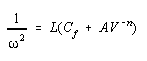 ............(3)
............(3)
Let ![]() be the angular frequency of the unmodulated carrier and Vo and Co be the corresponding
values of V and C. Then from Equation (3) we have
be the angular frequency of the unmodulated carrier and Vo and Co be the corresponding
values of V and C. Then from Equation (3) we have
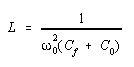 ............(4)
............(4)
If Vo is modulated by a small voltage V, the carrier will be deviated by a small frequency ![]() .
.
![]()
Substituting for L and rearranging, we have
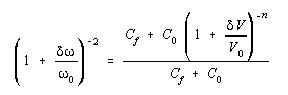
The oscillator tuning sensitivity K can therefore be written as
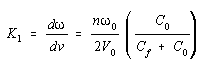
The units of K1 is rad/sec/volt.