Our design originated from a simple concept based on
amplifying the sum of an input signal and a feedback
signal to produce an error signal that would correct for
the nonlinearities inherent in audio speakers. An
accelerometer mounted on the speaker would give an
acceleration signal, and this signal would then be
integrated twice to obtain a "position" signal,
which would be fed back to the input. Our initial decision
to feed back position rather than acceleration or velocity
was based on the assumption that a speaker cone's position
is proportional to the voltage across its inputs.
Our initial test setup consisted of a small
dominant-pole amplifier powering a 20 watt woofer fitted
with a 5g accelerometer. The summing junction was
implemented by feeding the input signal into the
non-inverting input of an op-amp, and running the feedback
to the inverting input. Integration was accomplished with
two simple op-amp integrators (Figure 1): 
This setup oscillated fiercely and painfully when the
feedback loop was closed, and all attempts to alter the
gain and phase characteristics of the circuit failed to
eliminate the oscillation.
It was suspected that the high open-loop gain of the
input op-amp was contributing to oscillation. A second
approach involved two feedback loops, the weighted sum of
which would be fed back to the op-amp (Figure 2).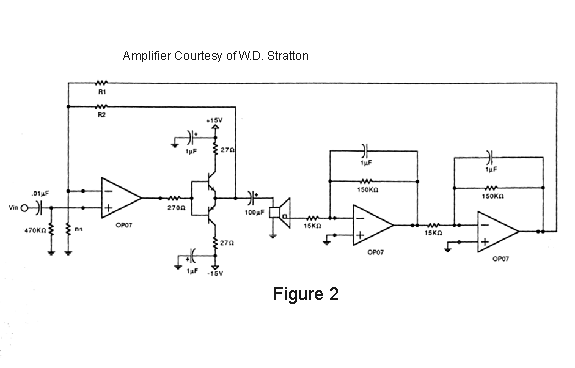 
The thinking was that the inner loop could help keep the
gain of the op-amp in check, while the outer loop provided
the desired position feedback. This succeeded in
eliminating oscillation, but it was soon determined that
the "inner" feedback loop completely dominated
the action of the feedback, so that the position signal
went essentially unused. Heavily weighting the position
signal when summing the two feedback loops again produced
oscillation.
Returning to the idea of a single feedback loop and
focusing on the problem of reducing the extremely high
gain of the summing junction op-amp, another idea that
seemed plausible was to replace the op-amp with a
differential amplifier. This would maintain the desired
differential operation, while allowing a choice of
open-loop gains. With the diff-amp in place, oscillation
no longer occurred as long as gain was kept close to
unity.
Originally, it was assumed that a microphone would be
used to determine the speaker output for THD measurement.
However, as our advisor pointed out, the accelerometer was
already measuring speaker cone movement more accurately
than a microphone could, so a microphone seemed somewhat
redundant. Measuring input at the function generator, and
output at the output of the double integrator, THD
measurements were taken. According to the results, THD was
worse with the feedback loop closed than open.
It was observed that for a sinusoidal input, with the
feedback loop open, and the speaker output distorted (by
placing small weights on the speaker cone), output from
the double-integrator was still a normal looking sinusoid.
That is, it was possible to feed a relatively distorted
sine-wave acceleration signal into the double integrator,
and get a clean (to the naked eye) sine-wave position
signal out. It was speculated that the double-integrator
was "smoothing" the acceleration signal in
addition to integrating, so that the circuit failed to
correct the distortion detected by the accelerometer.
Further support of this theory came from the fact that
integrators are, after all, low - pass filters, and the
corner frequency for ours was down at 1 Hz. A small
experiment was performed in which a signal with high
frequency components was fed into the double integrator,
and the output was observed. The high frequency components
of the signal were severely attenuated. This explained the
failure of the system with integration in place - the
frequencies that we wished to detect with the
accelerometer were being filtered out by the integrators.
Based on a suggestion given by our contact Jim Doscher
early on in the project, the double integrator was removed
from the feedback loop, so that the accelerometer output
was fed directly into the diff-amp. Justification for this
comes from the fact that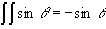 
, and from
fourier theory, which states that any given wave form can
be reproduced as the sum of a series of sine waves. If the
double integration is distributed across the fourier sum,
the result tells us that all we need to do to accomplish
"integration" is to invert the accelerometer
signal.
Alternatively, lack of integration can be justified by
the fact that the real purpose of the feedback loop is to
detect and cancel out unwanted frequencies. For a given
distorted signal, these frequencies are present in both
acceleration and position wave forms. Thus phase (the only
real difference between position and acceleration in this
case) is irrelevant.
With the integrators removed from the setup,
measurements showed that THD was reduced when using
feedback. Although THD, as well as the effectiveness of
the feedback loop, varies widely with input frequency, THD
was reduced by up to 50% at some frequencies.
, leading to K =
1.3x10-8. The peak at 345 rad/sec and the dip at 490 rad/sec correspond
to second order terms in the denominator and numerator, respectively.
Some tweaking with the damping factors resulted in a nice fit with our
experimental data. For the second half of the curve (w > 600 rad/sec),
we at first assumed another second order term in the denominator for the
peak at 900 rad/sec, followed by another in the denominator for the
slight downturn at 1450 rad/sec. This didn’t work very well. A closer
look at the response curve revealed that there was a slight change in
slope at 600 rad/sec. By adding a first order term in the denominator,
we improved the curve’s shape, but we were still unable to find the
correct damping factors for the peaks at 900 rad/sec and 1450 rad/sec.
We then decided to try squaring the second order term for 900 rad/sec.
This resulted in the desired shape of the curve, and we tinkered with
the damping factors until obtaining the final curve shown in Figure 5.
