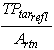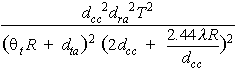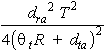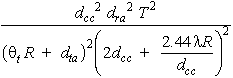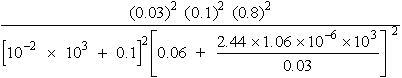| This version reflects the comments of the core participants as reviewed and incorporated in accordance with CORD's FIPSE-supported Curriculum Morphing Project. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
MODULE 6 (1)Lasers can be applied to a variety of important distance-measurement tasks. This chapter describes three such methods.
(2)A pulsed laser ranging system is a distance-measuring device that operates by transmitting a short high-power pulse toward the target. A photodetector in the ranging system receives a reflection of the pulse. By knowing the time interval required for the signal to travel from the transmitter to the target and back to the receiver, it is possible to calculate the distance from the ranging system to the target. (3)Laser distance-measuring systems are used for surveying, ground profile measurements, gun fire ranging measurements (military), altimeters, space radars, satellite and missile tracking, and industrial machine tool control. (4)This chapter will acquaint you with
(5)Before starting this chapter, you must know and use basic laser eye safety. You should have studied algebra, trigonometry, geometry, pulse circuits and digital systems. And you will need a knowledge of physical optics, especially interferometry. 
(6)Upon completion of this chapter, you should be able to do the following: 1. Describe, in terms similar to the text, the operation of pulsed time-of-flight ranging systems, beam-modulation telemetry systems and interferometric systems. 2. Define the following terms:
3. Draw a sketch of the waveforms for a pulsed time-of-flight ranging system. Identify the transmitter pulse, receiver pulse, round-trip transit time, and the threshold voltage for leading-edge detection. 4. Calculate a maximum pulse rate and the received power for a pulsed, noncooperative ranging system. 5. Calculate the maximum frequency and the range for a beam-modulation telemetry system. 6. Calculate an amount of displacement and a maximum measurable distance for an interferometric system. 7. Set up and operate a pulsed ranging system using a GaAs laser diode transmitter. Estimate the range accuracy and measure round-trip transit time between two points outdoors. Calculate the range from the measured round-trip transit time. DISCUSSION (7)Lasers are useful for several types of distance-measurement applications. These include military rangefinding, surveying and machine tool control. The diverse requirements of these applications mean that a variety of different methods and types of lasers are used. In this chapter we describe three of the most important types of laser-based distance measurement:
Pulsed Time-of-flight Method (8)This method uses lasers with short pulse duration and high peak power, such as Q-switched ruby and Nd:YAG. It commonly is used for applications such as satellite and missile tracking and military rangefinding. (9)These laser ranging systems are used to measure the distance (or range) between the source (where the ranging system is located) and some object, which we will call the target. This is accomplished by:
(10)Because we know the velocity of light, we can convert this time measurement into a distance from source to target. (11)A block diagram of this type of laser ranging system is shown in Figure 1. Fig. 1
(12)The electronic circuitry measures the interval from the time the signal leaves the laser transmitter until it is received back at the detector, and converts the result to a range. (13)The transmitter and receiver are both optical systems, that is, telescopes. The transmitting optical system acts as an antenna to reduce the divergence angle of the transmitted beam and to aim the beam at the target. The receiver optical system acts as an antenna to collect part of the reflected beam and to "condense" or focus it onto the detector. The design of these optical systems will be discussed in more detail later. (14)To establish the required transmitter power, detector sensitivity, and antenna size (optical aperture), we will discuss the geometrical factors that affect the relation between transmitted power and received power. In radar terminology, this relationship is called the "range equation." In the following discussion, we will study this equation in different forms as it applies to different types of targets. In each case, we will assume that the transmitted beam completely covers the entire area of the target that reflects or redirects the beam back to the source. The transmitter-to-target geometry of the radiation pattern is shown in Figure 2. Fig. 2
(15)In this figure, the beam is shown leaving the transmitter antenna with an aperture diameter, dta, and divergence angle, q t (radians). At the target plane, a distance R from the transmitter, the illuminated area from the transmitter is:
(16)The power density f tar within this area (assumed for simplicity to be uniform) is equal to the transmitter power divided by this illuminated area, and reduced by the atmosphere transmission T:
(17)The value of T varies from 0 to 1, depending on the amount of absorption and scattering of light by the atmospheric condition. For a beam propagating in space, T will have a value of 1. Equation 2 will be used to describe the power density at the target in two target cases—noncooperative and cooperative targets.
Noncooperative Target (18)A noncooperative target generally is regarded as a diffusely reflecting object (such as a rock, tree, building, or tank). The term "noncooperative" is used because the target has not been prepared in advance to enhance the reflected return of the transmitted beam. This means that the reflectivity, Y, at the laser wavelength of different targets can vary from less than 1% to almost 100%. When the reflectivity is not known and cannot be estimated, a value of 20% or 0.2 (absolute number) is generally used. (19)Since the target is assumed to be diffusely reflective instead of specular (like a mirror), the reflected beam will be scattered into a hemispherical pattern, with the maximum intensity reflected normal to the target plane and the intensity dropping to zero for rays reflected parallel to the target plane. (See Figure 3.) However, since the target usually will have many surfaces that lie in different planes, we will assume that the reflected power radiates uniformly into a hemisphere. Fig. 3
(20)By knowing the power density, f tar , on the target (Equation 2), the material reflectivity at the laser wavelength, U , and the projected area* of the target, we can calculate the transmitter power reflected by the target.
(21)This reflected power is radiated uniformly into a hemisphere and a fraction of it is received back at the receiver antenna. The power collected by the receiver antenna is equal to Ptarrefl multiplied by the atmospheric transmission factor, T, and the ratio of the receiver antenna area, Ara, to the area of a hemisphere with a radius equal to the range R.
Combining Equations 2, 3, and 4 gives
For long ranges (large R), dta can be neglected in comparison with the term Rq t , and Equation 5 reduces to:
We note that the power received, Pr , depends strongly on the range R, decreasing as the fourth of the range.
Cooperative Target (22)A cooperative target is one for which the reflectivity to the laser beam has been enhanced to give a higher return signal to the receiver. This usually is accomplished by placing a retroreflective device or material on the target. (See Figure 4.) Fig. 4
(23)A common retroreflector is the "cube corner reflector." This device is usually an optical prism in the shape of a pyramid with three plane faces orthogonal to each other. The characteristics of this prism are such that a light ray entering the nonorthogonal face will undergo total internal (specular) reflection at each of the other three faces. (See Figure 5.) After reflection from each of the three faces, the light ray will emerge from the same face that it entered. The exit beam will be parallel to the entrance beam. This means that the beam appears to have been reflected by a plane mirror whose surface is perpendicular to the beam axis. This type of reflector gives a return beam independent of the exact orientation of the prism, so that alignment is not critical. Fig. 5
(24)The emerging beam will have a divergence angle equal to the divergence of the intercepted rays from the transmitter plus diffraction effects due to the limited size of its aperture. (25)Assuming 100% reflectivity for the corner reflector, the returned power will be:
The divergence angle (q cc) of the return beam from the retroreflector is given by
From the divergence angle, the area of the return beam at the receiver can be calculated as follows, with the help of Equation 8:
The power density of the return beam at the receiver is
and the power received by the optical antenna (Pr) is
Combining Equations 2, 7, 8, 9, 10 and 11 gives:
For very long-range measurements, that is
Equation 12 reduces to
For short-range measurements, that is,
Equation 12 reduces to
(26)Comparing Equations 13 and 14, we see that the range equation is significantly different. At close range, the received power Pr is dependent on the inverse value of the square of the range (R2) and independent of corner reflector area. In contrast, at long range, the received power is dependent on the inverse fourth power of the range and on the fourth power of the corner reflector diameter (dcc4). At long ranges it is quite possible for the atmospheric transmission to be the dominant factor.
(27)Most range (or distance) measurements are made by counting the time for the optical signal to travel from the transmitter to the target and back to the receiver. This is called the round trip transit time (tr). Since the velocity of light is known, we can convert the time measurement into a two-way distance measurement according to the equation,
(28)The laser most often used for laser ranging is a Q-switched laser with a short pulse. The shorter the pulse, the more accurate the range measurement can be. The laser should have a high value of peak power, to increase the received power. Most rangefinders use a Q-switched ruby or Nd:YAG laser. (29)Usually a digital circuit, such as a time interval counter is used to measure tr . Precision ranging requires that this time be measured relative to a specific point on the pulse, e.g., the "leading edge." The leading edge of a pulse is the rising or buildup side of the pulse. This is called "leading-edge detection" and is shown in Figure 6. Fig. 6
(30)In reality, pulses with instantaneous rise times as shown in Figure 6 do not occur. Consequently, the "leading edge" for detection has to be defined more precisely. This is done by measuring time from a point on the leading edge where the signal voltage has reached a predetermined value. This is accomplished in the time interval counter with a threshold trigger circuit to start and stop the time counting. For example: The circuit might be designed to trigger the start and stop circuits in the counter when a positive increasing voltage reaches a value of 3.0 volts. A time sequence plot of leading-edge detection range measurement using a threshold detector is shown in Figure 7. Fig. 7
(31)One common source of error in leading-edge detection range circuits occurs if the voltage magnitudes of the transmitter and receiver pulses are not adjusted to the same value before they are sent to the time interval counter. The range error that this can cause is shown in Figure 8. From inspection of Figure 8 you can see that, if the receiver pulse amplitude is too high, the time interval measurement, t h, will be too short. In contrast, if the receiver pulse is too low, the time interval measurement, tl , will be too long. Fig. 8
(32)The maximum pulse repetition frequency (prf) of a pulsed ranging system transmitter is dictated by the requirement that the transmitter not send out another pulse until the echo from the previous one has been received. The purpose of this restriction is to avoid confusion in the pulses arriving at the time interval counter. A plot of maximum unambiguous range as a function of pulse duration frequency is shown in Figure 9. Fig. 9
(33)The accuracy of a pulsed ranging system is determined by three major factors:
(34)A very accurate pulsed laser ranging system may have a range accuracy of thirty centimeters for distances of the order of kilometers. (35)Now let us consider some of the components used in rangefinding systems. This discussion will be limited to a survey of transmitters, receivers and antennas for laser/electro-optical ranging systems. Electronic ranging circuits, range tracking loops, phase detectors, local oscillators, and digital clock circuits are beyond the scope of this chapter. (36)Most pulsed ranging systems use ruby, Nd:YAG, or semiconductor laser diodes. Since ruby laser systems operate in the visible wavelengths, they can use higher-efficiency detectors. Nd:YAG systems normally operate at a much higher repetition rate and even have been considered in the continuous pumped, Q-switched mode where the prf can be as high as 10 kHz. Laser diodes are of lighter weight and easy to lase. But they are limited (because of low power) to relatively short ranges and cooperative targets. (37)The receiver for a laser ranging system is a photosensitive detector that can accurately and reliably convert the incoming optical signal into an electrical signal for processing by the receiver electronics. In general, you can expect that a system with a transmitter operating at a wavelength in the UV or visible will use a vacuum photodiode or photomultiplier because of their high sensitivity and low noise figure. In the near IR, silicon photosensors and special vacuum photoemissive devices are used. (38)The primary purpose of the transmitter antenna is to reduce angular divergence. Figure 10 shows two arrangements for reflective optics. Figure 11 shows two arrangements for refractive optics. When the laser output is diffraction-limited, beam divergence is inversely proportional to the antenna aperture diameter as shown by Equation 16. Fig. 10
Fig. 11
From this equation, we can see that the larger the antenna diameter, dt , the smaller is the transmitter beam divergence q d. (39)Figure 12 shows three configurations for receiver antennas. The function of the receiver antenna is to gather as much of the return energy as possible and focus it onto the photodetector. To reduce the noise in the receiver, narrow-band optical filters usually are placed over the photodetector to eliminate sunlight and other sources of optical noise. Fig. 12
(40) (41)In one notable application, the distance to the moon was measured using a Q-switched ruby laser pulse transmitted through the telescope of an astronomical observatory. The targets were panels of retroreflectors left on the moon by Apollo astronauts. The results have led to a determination of the distance of the moon from the earth with a higher precision than had been possible previously.
Beam-Modulation Telemetry (42)Continuous wave lasers also are used in optical ranging systems. Since the transmitter output has a sine wave modulation, the method is called beam-modulation telemetry. Because of the single frequency component in the modulation, this technique sometimes is called tone ranging. A typical arrangement is shown in Figure 13. Fig. 13
(43)Range is determined by measuring the phase angle (f r) between the transmitted sine wave signal and the received sine wave signal. (See Figure 14.) This phase angle can be related to a time delay tr similar to that measured in the pulse-measurement technique. The relationship between phase angle delay f r , modulation frequency fmod , and time delay tr , is:
Fig. 14
Then, according to Equation 15, the range R will be:
(44)Just as in the case of pulsed time-of-flight systems, continuous beam-modulation telemetry systems have a maximum unambiguous range. This range is limited to that which causes a phase delay in the sine wave of one complete cycle. The equation for maximum unambiguous range Runamb in a CW system is:
(45)Highly accurate tone ranging systems often have several modulation frequencies or tones. The lower-frequency tones are used to prevent an ambiguous range measurement. The higher-frequency tones are used for more accuracy. (46)The accuracy of CW tone ranging systems is limited by
(47)There are CW tone-ranging systesms that use HeNe, argon, CO2, and other gas lasers as well as semiconductor laser diodes. The visible lasers offer the advantage of easy alignment and availability of high-efficiency detectors, whereas the CO2 laser can operate better in smog or haze. This type of distance-measurement system, which can have an accuracy better than 1 cm over distances of the order of kilometers, has been used for applications such as surveying and land profiling.
Interferometric Methods (48)Laser-based distance measurements can be done using interferometric principles. Measurements of length using optical interferometry have been performed since the 19th century. But the limited intensity and coherence of conventional light sources restricted the measurements, which were difficult and suitable for used only over distances of a few centimeters. The development of lasers removed these restrictions. Lasers have allowed interferometry to develop into a fast, highly accurate and versatile technique for measuring longer distance. (49)Interferometric measurement of distance can be highly accurate. It offers a higher degree of precision than the pulsed time-of-flight or beam-modulation telemetry methods. However, it is best suited to measurements made in a controlled atmosphere (for example, indoors) over distances no greater than a few tens of meters. (50)Most laser-based interferometric systems for measurement of distance use a frequency-stabilized helium-neon laser. An unstabilized laser, operating in a number of longitudinal modes, will have a total linewidth around 109 Hz. This spread in the frequency (or wavelength) will cause the interference fringes to become blurred and to lose visibility as the distance increases. An unstabilized laser is suitable for measurement only over distances of a few centimeters. Stabilized lasers, usually in a temperature-controlled environment and operating in a single longitudinal mode, are used for longer distances. (51)We describe first the operation of a system based on the Michelson interferometer, because it is easy to understand the basic principles of interferometer distance measurement with reference to the Michelson interferometer. Later we will describe variations that provide better stability under conditions of atmospheric turbulence. (52)Figure 15 shows the basic configuration for a Michelson interferometer. Review Course 5 on interference if necessary to understand the formation of an interference pattern. The beam from the laser falls on a beam splitter that reflects half the beam in one direction (the reference arm) and transmits the other half (the measurement arm). The two beams are each reflected by mirrors, a stationary mirror in the reference arm and a movable mirror in the measurement arm. In practice the mirrors are often cube corner reflectors (retroreflectors) which offer better stability against vibrations than conventional flat mirrors. Fig. 15
(53)The two reflected beams are recombined at the beam splitter to form an interference pattern that is viewed by an observer or measured by a recorder such as a photodetector. The character of the fringes is related to the different optical path lengths traveled by the two beams before they are recombined. (54)Suppose, for example, that the detector is viewing a bright fringe in the interference pattern when the movable mirror is at a certain position. If the movable mirror moves a distance equal to 1/4 of the wavelength of light, the round-trip distance traversed by the light in the measurement arm will change by 1/2 wavelength, and the fringe pattern will change so that the detector now views a dark fringe. The distance mesurement thus consists of counting the number of fringe variations as the mirror moves. Each complete fringe corresponds to a phase variation equal to 2p . The variation in phase d is determined by using the equation
where l is the wavelength of the light, and D x is the distance that the movable mirror has moved. It is apparent that this method offers high precision, allowing measurements of D x to be made with an accuracy of the order of a fraction of the wavelength of light. (55)The maximum distance D x that can be measured in this way is given by:
(56)This equation shows the importance of using a frequency-stabilized laser with a small line width. (57)Note also that this measurement is a relative measurement which gives the distance that the mirror has moved from its initial position, rather than an absolute positional measurement.
(58)The distance measured in an optical measurement is the optical path, which is the physical path multiplied by the index of refraction of the air through which the measurement is made. Since the index of refraction is close to unity, in some cases (for example, military ranging) it is not necessary to correct for variations in the index of refraction. But in interferometric measurements requiring a high degree of precision, one must correct for changes in the index of refraction that occur as a result of changes in air pressure, temperature, and so on. The index of refraction of dry air at a pressure of 760 Torr and a temperature of 15° C is 1.0002765 at the helium-neon laser wavelength. As conditions in the air change, the index of refraction changes. It increases by:
(59)So, a measurement system that requires high precision must include sensors for measurement of air temperature and pressure (an perhaps relative humidity) and a means (often an automated computer-based means) for correcting for the variable atmospheric parameters. (60)A schematic diagram of a system to measure the motion of a machine tool carriage is shown in Figure 16. The system uses two photodetectors to determine the direction of the motion. The two detectors collect light from different portions of the fringe pattern. The relative phase of the modulation of the fringes will be different, depending on whether the carriage is moving toward the laser or away from the laser. Fig. 16
(61)The interferometric technique described above was developed early in the laser era and was the basis of measurement systems used in the 1960s. It suffers the drawback of being very sensitive to turbulence in the air, which can wipe out the fringe pattern. This problem has been reduced by use of a two-frequency laser system that mixes two beams of different frequencies and measures the Doppler shift of the beam reflected from the moving mirror. This system, developed in the early 1970s, forms the basis for many modern interferometric distance-measuring systems. (62)The operation of such a system is shown in Figure 17. In this figure, f1 and f2 are the two laser frequencies, and D f1 is the Doppler shift produced by the motion of the retroreflector. Fig. 17
(63)The helium-neon laser emits light at two slightly different frequencies, f1 and f2 , with different polarization properties. The laser has an axial magnetic field that splits the fluorescent line of neon into two differently polarized frequency components separated by about 2 MHz. (64)A polarization-sensitive beam splitter separates the two frequencies so that they
travel different paths. Light with frequency f2 is sent to a fixed
reflector. Frequkency f1 goes to the movable reflector attached to the
part whose distance is to be measured. If the part moves with velocity v, the
frequency f1 upon reflection changes by an amount
(65)This shift is due to the Doppler effect and is analogous to the familiar Doppler effect in acoustics. The two beams with frequencies f1 + D f1 and f2 are recombined by the beam splitter and sent to a detector. The output of the detector will contain an oscillating component at frequency f1 + D f1 – f2, which can be compared to the original difference frequency f1 – f2, generated at a second detector. This gives a measurement of D f1 and hence of v, according to Equation 22. The value of v then can be integrated over time to yield the total displacement. (66)This type of system is not highly sensitive to degradation produced by air turbulence, air motion, and so on. It can provide measurements of motion in the one-millionth-inch regime in an industrial environment. (67)Accurate laser-based interferometric measurements have been applied in a wide variety of practical cases in industry, such as:

1. Describe, in terms similar to the text, the operation of the following distance-measurement systems: · Pulsed time-of-flight · Beam-modulation telemetry · Interferometric 2. Define the following terms: · Noncooperative target · Cooperative target · Unambiguous range · Round-trip transit time · Leading-edge detection 3. Draw a sketch of the waveforms for a pulsed time-of-flight ranging system. Identify the transmitter pulse, receiver pulse, round-trip transit time and the threshold voltage for leading-edge detection. 4. A Nd:YAG laser that emits pulses with peak power 105 watts is aimed at a noncooperative target with diffuse reflectivity of 0.3 and diameter of 3 meters at a distance of 1.5 km. The beam divergence angle is 100 milliradians, and the receiving telescope has a diameter of 12 cm. Assume that the atmospheric transmission is 90% over the range. What is the peak value of the received power? What is the maximum pulse repetition rate you could use? 5. A beam-modulation telemetry system measures the distance to a surveying pole. The operating frequency is 5 ´ 105 Hz, and the phase angle delay is 1.2 radians. What is the distance to the pole? What is the maximum value of the modulation frequency that could be used?6. A HeNe laser operating in a single longitudinal mode, and with a line width of 1.2 ´ 107 Hz, is used to measure distance in a Michelson interferometer arrangement. The detector observes a shift of one-half fringe (i.e., a change from minimum intensity to maximum intensity) as the movable mirror is displaced slightly. How far did the mirror move? What is the maximum distance that you could measure with this apparatus?
Gallium arsenide laser diode Pulse generator Transmitter optics Pulser for GaAs diode Two alignment telescopes Two corner reflectors, 1" diameter and 3" diameter Receiver photodetector Receiver optics Oscilloscope, Tektronix 545 or equivalent Polaroid camera for oscilloscope Tripod Alignment telescope Timer interval meter Sheet of white paper, four feet square CW power meter Optical attenuator filter, 3 db @ 900 nm Narrow-band transmission filter, l = 900 nm
1. Set the pulse generator for __ * __ volt pulses, __*__ m sec wide, and at a pulse repetiton frequency of 100 kHz. Check for proper operation using the oscilloscope.2. Connect the pulse generator to the pulser and the laser diode. Set up the photodetector to record the output waveforms from the laser diode. 3. Measure the average output power from the laser diode. Record data. 4. Connect the laser diode to the output optics and a sighting telescope. Mount the transmitter assembly on a tripod. 5. Connect the receiver to the input optics and the sighting telescope. Insert the transmission filter. Connect the receiver to a power supply and oscilloscope. Block the input optics and measure dark current noise. Mount the receiver assembly on a tripod. 6. Position the equipment approximately 30 meters from a 0.1-square-meter white paper target inside the building. 7. Align the system on target and measure the return signal level from the photodetector. Record. Attempt to measure range using a time interval counter. 8. Position the equipment outside, approximately 300 meters from a one-square-meter, white paper target. Repeat Step 7. Record data. 9. Replace the paper target with a corner cube reflector. Repeat Step 8. Record data. 10. Extend the range to 1000 yards, repeat Steps 7 and 9. 11. Convert the average power measurement in Step 3 and the output waveform recorded in Step 2 to peak pulse power. 12. Using the peak transmitted power calculated in Step 11, calculate the received power in Step 10 using the white paper ( U = 1.0) and the corner reflector. Calculate the maximum unambiguous range.
Bachman, C.G. Laser Radar Systems and Techniques. Dedham, MA: Artech House, 1979. Beheim, G., and K. Fritsch. "Range Finding Using a Frequency-Modulated Laser Diodes," Applied Optics 25, 1439, May 1, 1986. Edwards, B.E. "Design Aspects of an Infrared Laser Radar," Lasers and Applications, 47, October 1982. Gillard, C.W.; N.E. Buholz; and D.W. Ridder. "Absolute Distance Interferometry,"Optical Engineering 20, 129, January/February 1981. Gillard, C.W., and N.E. Buholz. "Progress in Absolute Distance Interferometry," Optical Engineering 22, 348, May/February 1983. Greve, A., and W. Harth. "Laser-diode Distance Meter in a KERN DKM 3A Theodolite," Applied Optics 23, 2982, September 1, 1984. Luxmoore, A.R. Optical Transducer and Techniques in Engineering Management, Chapter 5. London and New York: Applied Science Publishers, 1983. Luxon, J.T., and D.E. Parker. Industrial Lasers and Their Applications, Chapter 10. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1985. Ready, J.F. Industrial Applications of Lasers, Chapter 10. New York: Academic Press, 1978. --------------------------------------------------------------
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
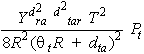
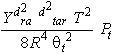
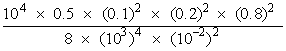 watts
watts +
+