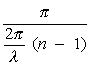| This version reflects the comments of the core participants as reviewed and incorporated in accordance with CORD's FIPSE-supported Curriculum Morphing Project. | ||||||||||||||||||||||||||||
MODULE 10-7 INTRODUCTION The Mach-Zehnder interferometer is an important diagnostic tool. It is most frequently used in the fields of plasma physics, aerodynamics, and heat transfer to measure density, pressure, and temperature changes in gases. Because of its relatively large and freely accessible working space and flexibility of location of the fringes, it is the most suitable interferometer to study the airflow around models of aerodynamic structures. This module will familiarize the student with the characteristics of the Mach-Zehnder
interferometer and some of its applications. It will also give practical experience in
building, aligning, and using this versatile optical device. MODULE PREREQUISITES The student should have completed Module 1-1 through 1-6 of Course 1, "Introduction to Lasers"; Modules 6-1 through 6-8 of Course 6, "Laser and Electro-Optic Components"; and have a basic knowledge of laser safety, including eye hazards and electrical safety, as well as knowledge of algebra and interference of optical waves. The student should also be able to operate a HeNe laser and adjust a beam-expanding telescope. 
Upon completion of this module, the student should be able to: 1. Demonstrate knowledge of Mach-Zehnder interferometers by drawing and labeling a diagram as shown in the text. Explain the basic design of the instrument and how it operates, including the following items:
2. Assemble a Mach-Zehnder interferometer and align the interferometer using a HeNe laser and beam-expanding telescope according to procedures outlined in the text.. 3. With the Mach-Zehnder interferometer as previously assembled, perform experiments according to given procedures to accomplish the following tasks:

The Mach-Zehnder interferometer is basically a very simple device. A schematic diagram of the instrument and associated optical equipment is shown in Figure 1. The light beam from a source, say a HeNe laser, is first expanded by a telescope. The expanded laser beam is divided at the 50% reflecting/50% transmitting surface of a plane parallel glass plate P1 into two beams of equal intensity. After reflection at the 100% reflecting plan mirrors M1 and M2, the two beams are recombined at the 50% reflecting/50% transmitting surface of plane parallel plate P2. The recombined beams emerge from P2 and are intercepted by a well-corrected positive lens L2, which brings both beams to the focus at S¢ . This will always be true if the four reflecting surfaces, whose centers are at the corners of a parallelogram, are perfectly parallel. (Figure 1 shows a rectangle which is a special case of the parallelogram.) Fig. 1
When all reflecting surfaces are perfectly parallel, the recombined beams do not produce interference fringes. If, on the other hand, the four reflecting surfaces are only approximately parallel, the recombined beams will interfere and produce interference fringes. The exact location of the fringes depends on the size of the light source S and the relative alignment of the four reflecting surfaces. Let us briefly consider the mechanism of interference as it applies to the Mach-Zehnder interferometer. The two beams of light of equal amplitude and wavelength originating from the same source are brought to a focus at S¢ and S² if the reflecting surfaces are nearly parallel to each other. As indicated in Figure 2, the light from the images S¢ and S² proceeds on, and the beams interfere in much the same way as in Young’s famous double slit experiment. In a plane (the screen) at a right angle to the direction of propagation of the combined beams, an interference fringe pattern will be observed. This means that bright lines will be seen where the peaks of the waves reinforce and dark lines where the troughs of the waves from one beam coincide with the peaks of the waves from the other beam. The end result is a series of nearly parallel light and dark lines varying sinusoidally in intensity. If the intensity were measured as a function of position across the beams, the pattern shown in Figure 2b would be observed. Fig. 2
If the reflecting surfaces are adjusted so that the images S¢ and S² lie on a horizontal line (into the paper), the fringes will be vertical; if S¢ and S² lie on a vertical line (in the plane of the paper), the fringes will be horizontal. Fringe spacing—that is, the distance between light lines (or dark lines)—depends on the distance between S¢ and S² . For instance, fringe spacing can be increased (more nearly equal path lengths) by adjusting one mirror in such a way that the distance between S¢ and S² is decreased. If lens L2 is removed, fringes will still be observed, but the coherent sources S¢ and S² are now virtual and located at infinity. What happens to the fringes if the length of the optical path of one of the beams is changed (say the test beam P1M2P3 in Figure 1) by inserting a plane parallel glass plate into the path of the beam? By causing one beam to propagate through the plane parallel glass plate, a new phase shift is introduced between S¢ and S² which causes a shift of the fringes. The extent of the shift is a sensitive measure of the change of the optical path length over the two dimensional fields of view. For example, by inserting a glass slide only 0.0002 millimeter thick into one of the beams (which is assumed to originate from a HeNe laser at 632.8 nm), the fringe pattern would reverse itself; that is, the dark and light lines would exchange positions. Example A demonstrates how the Mach-Zehnder interferometer can be used to calculate the thickness of a glass slide that will cause a reversal in the fringe pattern.
Let us illustrate the sensitivity of this device with one more example. The index of refraction of fluids depends on the temperature, among other things. If we fill a cell of length L = 10 cm with water and insert this cell into the test volume between M2P2 and an identical air-filled cell into the path M1P1 of Figure 1, and raise the water temperature by 1/20°C, we would observe a full shift of one fringe corresponding to an optical path length change D nL of l (l = 632.8 nm). Since 1/10 fringe shift can be accurately measured, it is possible to measure temperature changes of water by as little as 1/200°C. Thus, the interferometer can act as a very sensitive thermometer. Before turning our attention to the more technical aspects of the Mach-Zehnder interferometer, such as its construction, alignment, and use, let us discuss one final but very important characteristic of this device. If, instead of the well-collimated beam which is essentially derived from a point source, we had to work with an extended source of light, fringes may still be observed. But now they will be sharp only in a particular plane. The reason for this is that instead of the two coherent point images S¢ and S² in Figure 2, we now have many pairs of coherent points, covering the whole extent of the images centered about S¢ and S² . It is possible to show that for extended sources, fringes are located in the region in which the two emerging rays originating from the same incident may meet. This principle is illustrated in Figure 3a where mirror M2 has been rotated counterclockwise by a small amount. Fig. 3
It can be seen that only the reflected beam to P2 will be affected. The reference beam propagating through the outer part of the interferometer is not affected and arrives at P2 as before. The beams of light indicated by rays 1 and 2 emerging from P2 will no longer intersect. However, by extending both rays back through beam splitter P2, as is done in Figure 3a, it can be seen that the virtual rays intersect at a point between M2 and P2. The region where these virtual rays meet becomes the virtual region of fringe localization. This region of fringe localization can be moved anywhere between mirror M2 and beam splitter P2 by simply rotating P2 clockwise a small amount. The effect of a small rotation of P2 on the virtual location of the fringes is shown in Figure 3b. In this way, one can actually place the fringes at infinity or before or behind beam splitter P2. This flexibility in fringe localization gives the Mach-Zehnder interferometer one very important advantage over many other interferometers. For instance, when the Mach-Zehnder interferometer is used for the examination of airflow around a section of an aircraft wing, a model of the wing is enclosed in a test cell that is located in one leg of the interferometer. Once the model is in position, a high-velocity airstream is blown past it. The airstream forms a pressure pattern around the model which causes local changes in the index of refraction which, in turn, can be measured from the resultant change in the fringe pattern. For this kind of experimental work, it is necessary to photograph both the interference fringes and test model simultaneously so that both are in focus. Therefore, it is necessary that the fringes be located (or localized) in the region where the test object is located. The plane where the object and the fringes more or less coincide can now be imaged on a screen or on a photographic plate. In the case of a wind tunnel or shock-wave tube experiment, photographs of the fringe pattern are obtained with and without gas flow. The change of fringes, that is, the number of times the intensity at a selected point P changes from say bright to dark to bright, is counted. This number, which is designated by D m, is given by Equation 1.
In summary, the use of the Mach-Zehnder interferometer has increased considerably since the advent of the laser. This is attributed to the laser beam’s unique properties of brightness and coherence length, which have greatly simplified the alignment and use of the Mach-Zehnder interferometer. 
Helium-neon laser (1-5 milliwatts, TEM00 mode) Beam-expanding telescope 4 gymbaled mirror mounts for approximately 5 cm diameter optics (micrometer adjustment) 2 plane parallel glass plates (optical grade) to fit gymbaled mount, coated with 50% reflecting /50% transmitting aluminum coating 2 plane front surface mirrors to fit gymbaled mount Piece of white cardboard to be used for screen Slab of hardened aluminum, stainless steel, or granite (approximately 2 cm ´ 50 cm ´ 30 cm) Foam rubber sheet (same dimensions as slab) Optical table, 4 ´ 8 feet with vibration isolation (Ealing 22-4428) Tube of airplane glue used to fasten gymbaled mounts onto slab Vacuum pump 2 needle valves Cylindrical absorption cell with flat windows (5 cm long) Plane parallel glass plate to be tested for polishing inaccuracies Zoom telescope (approximately 60 power), optional Piece of diffusing glass and one neutral density filter (ND = 1.0) Pressure vacuum gauge 632.8 nm filter Candle 
Before beginning the experiment, the student should review the safety procedures that apply when using the HeNe laser. The student will perform three experiments: 1. Assemble a Mach-Zehnder interferometer and align it with a HeNe laser. 2. Measure the refractive index of air using the Mach-Zehnder interferometer. 3. Observe and measure the optical figure inaccuracies of a flat plate of optical quality glass using the Mach-Zehnder interferometer. EXPERIMENT 1: Building a Mach-Zehnder Interferometer. Although many Mach-Zehnder interferometers use a rectangular arrangement, the parallelogram arrangement shown in Figure 4 has certain advantages. For one, the effect of imperfections in the optical flats used for the 50% reflecting mirrors decreases with decreasing angle of incidence of the light beams on these flats. Another reason is that the aperture, or useful field width to mirror width, increases as the angle of incidence is reduced. We will select a parallelogram arrangement with an acute angle of 60 ° , giving an angle of incidence of 30° .Fig. 4
Before proceeding with the construction of the interferometer, it is important that the instrument be isolated from vibration. The success of future measurements will depend on how well this isolation is accomplished. An acceptable procedure is to mount the four mirror holders on a slab (approximately 2 cm thick) of hardened aluminum (tool plate), stainless steel, or granite. To isolate the instrument from vibration, a sheet of foam rubber (several centimeters thick) with approximately 2 cm diameter holes punched through it is placed between the slab and the supporting table. The purpose of the holes in the foam rubber sheet is to provide isolation from lateral motion. The table should rest on air-inflated rubber tubes or bags. Depending on the construction of the building and its location, this combination is generally adequate. To minimize thermal expansion, the instrument should be located in a room where the temperature is well controlled and remains stable over several hours. Additionally, the flow from air conditioning ducts should be deflected from that part of the room where the interferometer is located. The first step in the construction of the Mach-Zehnder interferometer is to draw a parallelogram, such as the one shown in Figure 4, on the slab resting on the foam rubber sheet. Allow sufficient space on the table for the HeNe laser and beam-expanding telescope. Following Figure 4, arrange the two front surface mirrors and two 50% reflecting mirrors so that the vertical axis of rotation of the reflecting surfaces coincides with the corners of the parallelogram. To maximize the quality of the fringe pattern, the plates should be flat to a twentieth wave, and the inhomogeneity of the beam splitters in the index of refraction should be better than 5 parts in 106. Next, align the HeNe laser (which should be operating in the TEM00 mode) and beam expander so that the center of the expanded laser beam coincides with the centers of the 50% reflector P1 and the 100% reflector M1. Now, adjust M1 so that the reflected beam is centered on P2; adjust P1 so that the reflected beam is centered on M2; and, finally, adjust M2 so that the reflected beam is centered on P2. After a few additional fine adjustments of the reflecting surfaces, the two beams should completely overlap at the output surface of P2. At this point, fringes should be observed on the screen after final adjustments have been made by slowly rotating P2. The fringe spacing can be controlled with fine adjustment of only M2 and P2. This completes the assembly and alignment of the Mach-Zehnder interferometer. EXPERIMENT 2: Measurement of the Refractive Index of a Gas. One of the simplest experiments involves the measurement of the index of refraction of a gas with an airtight test cell placed in one of the optical arms of the Mach-Zehnder interferometer. This experiment is particularly easy when a laser is used instead of some more conventional light source, such as a sodium lamp or a high-pressure mercury vapor lamp. Figure 5 illustrates the experimental setup. The interferometer is aligned as described in the previous experiment. Next, the test cell is evacuated and positioned in one optical arm. If the fringe spacing is too small, a positive lens may be placed between plate P2 and the screen. By adjusting the position of the screen, the fringe pattern can be magnified several times. This permits a more clearly visible pattern and reduces eye strain when it becomes necessary to count the moving fringes. Fig. 5
The measurement begins by closing off the valve connecting the vacuum pump to the evacuated test cell and slowly opening the needle valve which permits the gas, whose index of refraction is to be measured, to enter the cell. As soon as the gas enters the cell, the fringes begin to move and must be counted as they go past a reference mark on the screen. With some care, even fractional parts of a fringe can be measured quite accurately. The refractive index n at the particular wavelength l is then computed using Equation 2.
A typical measurement for air at STP with a test cell of L = 5 cm, l = 632.8 nm, and D m = 21 resulted in an index of refraction of 1.000253. This procedure can be repeated at several pressures and a plot of refractive index versus pressure obtained. EXPERIMENT 3: Measurement of the Polishing Inaccuracies with a Mach-Zehnder Interferometer. In the preparation of optically flat plates, it becomes necessary to check the specimen periodically for flatness. This is generally done by laying the specimen on an optical flat and viewing the fringes under a mercury lamp. This test for flatness or polishing inaccuracies of an optical plate can also be performed with the Mach-Zehnder interferometer. For such a measurement, it is necessary that the fringes be localized at the position of the specimen, normally between M2 and P2, as discussed previously, so that they both can be focused on the screen or photographic plate. Therefore, the plane of the fringes must be moved to the plane of the specimen. This adjustment is performed by rotation of both M2 and P2 and is largely done by trial and error (and a great deal of patience). This time-consuming adjustment can be accomplished more quickly with the help of a high power zoom telescope (around 60X). A diffusing plate of glass must be placed at the exit end of the beam-expanding telescope. A neutral density filter is placed between the HeNe laser and the beam-expanding telescope (see Figure 6). (At this point, particular caution must be exercised to reduce the light intensity in order to avoid eye damage.) The zoom telescope is then focused through plate P2 on the specimen. Using the low magnification, the depth of field of the telescope may be sufficiently large that both the specimen and fringes are in focus. Plate P2 is slowly rotated to bring the fringe plane closer to the specimen. The magnification of the telescope is now increased, which reduces the depth of field. Plate P2 is again adjusted to move the fringe plane closer to the location of the specimen. At the final maximum magnification, the fringes can be located to within a few centimeters of the specimen. This procedure will ensure maximum resolution and sharpness of fringes. This completes the alignment of the interferometer. Fig. 6
The final step in this experiment consists of an examination of the fringe pattern at the specimen. Depending on the polishing imperfections, the fringe pattern may resemble a contour map. The difference in the thickness D L from one point to another point on the specimen is determined by counting the number of fringes D m between these two points and using Equation 3.
A specimen that exhibits a fringe field of evenly spaced straight fringes, with a fringe spacing and orientation that is equal to the fringe spacing of the background fringe field surrounding the specimen, has flat and parallel surfaces and no polishing inaccuracies. EXPERIMENT 4: Use of Mach-Zehnder Interferometer in Flow-Visualization. If the student has sufficient time remaining, it would be instructive to exhibit the use of the Mach-Zehnder interferometer for flow-visualization applications. Employing the already assembled instrument, a candle is placed in the test volume. The heat generated by the burning candle generates an air current directly above the flame. (The room air should be quiescent to prevent too much turbulence.) A fringe pattern should be visible around and above the candle flame. However, the luminosity of the flame itself may make the fringes difficult to see. This can be eliminated in two ways–first, by placing the candle flame below the field of view of the interferometer so that only the air motion above the candle is seen. A second technique is to place the candle in the field of view and examine the flame pattern through a 632.8 nm filter. In this manner, it is possible to discriminate between the undesirable luminous candle and the probe HeNe laser light, affording a greatly increased capability. This technique of light discrimination is frequently employed with highly monochromatic light sources used in interferometry. 
1. Explain, with appropriate drawings, the basic optical design of a Mach-Zehnder interferometer. 2. Explain the operation of a Mach-Zehnder interferometer. Include statements on how the basic interference (fringe) pattern is formed, the effect that the insertion of a glass plate in one of the arms has on a glass plate, the reason for fringe localization, and the use of fringe localization in examining airflow around aerodynamic structures. 3. Give appropriate drawings of the necessary optical arrangements in a Mach-Zehnder interferometer to accomplish the following:
4. A Mach-Zehnder interferometer is used to measure the index of refraction of a certain gas mixture. As the gas fills the 2 cm long gas cell, a total of 17 fringes is counted as they go past a reference mark on the screen. A HeNe laser is used as the light source. What is the index of refraction of the gas? 5. A thin film of soapy water on a wire loop is inserted into the test volume of a Mach-Zehnder interferometer so that the film is perpendicular to the HeNe laser probe beam. After mirror P2 has been adjusted for fringe localization, a photograph of the fringe pattern is obtained (see figure). Calculate the change in thickness between the top and bottom of film. Explain why the soapy water film is thicker at the bottom. This conclusion cannot be drawn from a study of fringe pattern alone. The index of refraction of the soapy water is 1.4. 
Francon, M. Optical Interferometry. pp. 97-99. New York: Academic Press, 1966. Gebhard, B. and Knowles, C. P. "Design and Adjustment of a 20 cm Mach-Zehnder Interferometer." The Rev. of Sci. Inst., 37 (1), Jan. 1966, pp. 12-15. Hariharan, P. "Modified Mach-Zehnder Interferometer." Applied Optics, 8 (9), Sept. 1969, pp. 1925-1926. Hecht, E. and Zajac, A. Optics. p. 292. Reading, MA: Addison-Wesley Publishing Co., 1974. Jackson, R. A. "The Laser as a Light Source for the Mach-Zehnder Interferometer." J. Sci. Instrum., 42, 1965, pp. 282-283. Johnstone, R. D. M. and Smith, W. "A Design for a 6 in. Mach-Zehnder Interferometer." J. Sci. Instrum., 42, 1965, pp. 231-235. Ludman, J. E. "Measure Parallelism with an Interferometer." Optical Spectra. December 1980, p. 45. Mach, E. The Principles of Physical Optics. pp. 170-172. New York: Dover Publication, Inc., 1973. Price, E. W. "Initial Adjustment of the Mach-Zehnder Interferometer." The Rev. of Sci. Inst., 23 (4), April 1952, p. 162. Steel, W. H. Interferometry. pp. 91-93. London: Cambridge University Press, 1967. Tolansky, S. An Introduction to Interferometry. pp. 115-116. London, New York, Toronto: Longmans, Green and Co., 1955. Winckler, J. "The Mach-Zehnder Interferometer Applied to Studying an Axially Symmetric Supersonic Air Jet." The Rev. of Sci. Inst. 19 (5), May 1948, pp. 307-322. --------------------------------------------------------------
|
||||||||||||||||||||||||||||