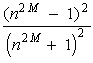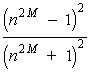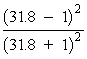INTRODUCTION

The Fabry-Perot interferometer has many uses in conjunction with lasers and is of considerable importance in modern optics. In its simplest form, the Fabry-Perot interferometer consists of two parallel mirrors, called a Fabry-Perot etalon, which has optical resonator properties similar to those of the laser itself. The spherical mirror Fabry-Perot interferometer is an instrument which is often used in high resolution optical spectroscopy. It is also a common tool for the analysis of laser radiation. These instruments can be used to determine and/or reduce the linewidth of optical sources.

The beam from a laser may appear to have a single color; however, it generally contains several discrete optical frequencies corresponding to different modes of oscillation of the laser resonator. The modes are separated from each other by approximately 10⁶ to 10⁹ Hertz. In many applications, it is necessary to know how many modes are oscillating; it may even be necessary to limit the number of modes that are oscillating in the laser. The Fabry-Perot interferometer can be used for this purpose. For example, in holography, several modes oscillating simultaneously in a laser limit the coherence length of the laser beam and, thus, limit the depth of field of the hologram made with that laser.

MODULE PREREQUISITES

The student should have completed Modules 1–1 through 1–8 of Course 1, "Introduction to Lasers"; Module 6-5, "Mirrors and Etalons"; Module 10-4, "Michelson Interferometer"; and have a basic understanding of algebra and trigonometry. The student should also be able to operate an oscilloscope, helium-neon and argon lasers, and be familiar with appropriate safety precautions.

Upon completion of this module, the student should be able to:

1. Describe the basic components of the Fabry-Perot interferometer, including the following:

a. Two reflecting surfaces.

b. Piezoelectric transducer/etalon spacer.

c. Photodetector.

2. Explain how the spherical mirror Fabry-Perot interferometer operates and how it differs from the simple plane mirror Fabry-Perot etalon. The explanation should include the following:

a. Multiple reflections between the surfaces.

b. Constructive interference between emerging rays to form transmission maxima.

c. Formation of a circular pattern of rings.

3. Demonstrate an understanding of the mathematical relationship governing transmission through an etalon by calculating the order of the interference for a given wavelength, etalon spacing, and direction of light.

4. Set up a scanning Fabry-Perot interferometer and use it to display the spectrum of a laser on an oscilloscope.

5. Adjust a laser to operate in a single transverse mode. The mode structure will be displayed on an oscilloscope.

6. Use the scanning Fabry-Perot interferometer to adjust the argon laser’s intracavity aperture so that the laser operates in a single transverse mode.

7. Adjust the intracavity etalon so that the argon laser operates in a single longitudinal mode.

In its simplest configuration, the Fabry-Perot etalon consists of two plane, parallel, highly reflecting surfaces separated by some distance d. The reflecting surfaces are formed by a very thin silver or aluminum film, or multi-layer dielectric films on the surface of glass plates. The enclosed air gap generally varies from several millimeters to several centimeters when the device is used interferometrically. If the gap can be mechanically varied by moving one of the mirrors, the device is referred to as an interferometer. If the mirrors are held fixed and adjusted for parallelism by screwing down on some kind of spacer (invar or quartz are commonly used), it is said to an etalon.

The various parts of the etalon are shown in Figure 1. Note that the outer surface of each plate is at a wedge angle and may be antireflection coated so that light reflected from these surfaces will be minimized. The wedge angle in Figure 1 is exaggerated. The gap between the reflecting surfaces need not be air; indeed, if the two surfaces of a single quartz plate are appropriately polished and silvered, it too will serve as an etalon.

The Fabry-Perot etalon is very important in laser technology. The optical resonator in most lasers is a Fabry-Perot interferometer. Its contributions to laser operation have already been described in Modules 1-7 and 1-8. In this module, the Fabry-Perot etalon will not be considered as a laser element. Rather, it will be considered as an accessory to perform a variety of tasks in optics and spectroscopy.

Figure 2 shows how the Fabry-Perot etalon is used. It receives the light from a broad source, which might be a mercury arc or a helium-neon laser beam spread out in diameter to several centimeters. This can be done by using a beam expander. The light can then be made diffuse by passing it through a sheet of ground glass. Figure 2 shows one ray as it propagates from some point S₁ on the source through the etalon. Entering by way of the partially silvered plate, it is multiply reflected within the gap. The transmitted rays are focused onto a screen, where they interfere either constructively or destructively.

The Fabry-Perot etalon operates by multiple beam interference. Light which is incident from the left on the first reflection surface is split by reflection into a series of parallel transmitted rays (Figure 3). The ray is partially transmitted at each reflection from the second surface. For simplicity, Figure 3 does not show the change in direction of propagation of light upon refraction, nor does it show the rays that pass back through the first surface and propagate toward the left.

When the difference in optical path length between the rays transmitted at successive reflections is such that the emerging waves are in the same phase, constructive interference will occur and the etalon will show a maximum in transmission. If this condition does not hold, the interference between successive emerging rays will be destructive and the transmission will be relatively low. It is common practice to incorporate a lens and viewing screen when using the Fabry-Perot etalon, as shown in Figure 2 and 3. This necessary for bringing rays to a common point before the results of the interference can be detected.

The condition for producing a maximum in transmission is given by
Nl = – AD; where , for example, is the optical path length between A and B in Figure 3. With the aid of some trigonometric relationships, the condition becomes:

The product nd is referred to as the optical thickness or optical length to distinguish it from mechanical thickness or length. Because the optical wavelength is usually much smaller than the physical separation between the reflecting surfaces, the integer N will be large, usually on the order of 10,000 to 100,000 depending on the mirror separation. The integer N is the order of the interference. In most cases of interest, the medium between the reflecting surfaces will be air and, for the remainder of this discussion, the index of refraction n will be taken to be unity.

For a given angle of incidence, the transmission as a function of wavelength is shown in Figure 4. If Equation 1 is satisfied by a particular combination of an integer N_o and wavelength l _o, the interference between the transmitted rays will be constructive, and there will be a maximum of transmission. At other combinations, for example N_o + 1 and l _o – D l , Equation 1 will also be satisfied and there will be another maximum of transmission. This situation is exactly analogous to the longitudinal modes of a laser cavity which have been described previously. The spacing D l between maxima of transmission is:

This is the same expression that holds for the spacing of laser modes.

Figure 4 also shows how the reflectivity of the surfaces affects the transmission. If the reflectivity is relatively low, the maxima in transmission will be broad. On the other hand, if the reflectivity is high, the maxima of transmission will be very narrow and sharp.

This leads to the concept of the finesse of the interferometer. The finesse is a measure of the interferometer’s ability to resolve closely spaced spectral lines. The finesse F is defined by Equation 3.

Example A demonstrates how Equation 3 can be used to find the finesse of the interferometer.

Example A: Calculation of the Finesse
Given:	The reflectivity of the mirrors’ surfaces of a Fabry-Perot interferometer is 95 percent.
Find:	The finesse of the interferometer.
	F =	(Equation 3)
Solution:	= = F = 61.2

As the reflectivity approaches unity, the finesse becomes very high. For high reflectivity, the transmission maxima are narrow, so that the transmission of maxima of slightly different wavelengths can be easily distinguished. Because of this capability, the Fabry-Perot interferometer can be used as a high resolution spectrometer. In fact, the resolving power RP is given the equation:

As one can see, for highly reflecting mirrors (R » 1), the finesse becomes very large—a desirable result. As R decreases, the finesse also decreases. In a plane parallel Fabry-Perot interferometer, the diffraction losses are quite large. In effect, these diffraction losses decrease the reflection coefficient R, thereby limiting the finesse of this type of interferometer.

Let us now consider the transmission as a function of angle for monochromatic light incident on the interferometer. For this fixed wavelength, there will be a number of different angles at which Equation 1 can be satisfied for successive values of the integer N. Since this can occur at any orientation of the angle q from the normal direction, the transmission maxima take the form of circular rings. That is, the condition described by Equation 1 is fulfilled by all points on the circle with a constant value of the angle a relative to the optical axis of the interferometer. Each ring corresponds to a different value of the integer N. When the angle q is increased, the cosine will decrease until another maximum is reached for which N is smaller by 1. This leads to a series of concentric rings, as illustrated in Figure 5. If more than one wavelength is present, the ring pattern will be a multiple pattern, as illustrated in Figure 6 for the case of two wavelengths, l ₁ and l ₂. The adjacent maxima are of the same order, i.e., the same value of N. However, this is not always the case, particularly if the wavelengths are well separated. If the wavelengths are separated by more than one order of interference, one has the situation of overlapping orders. Here, two adjacent rings for two widely different wavelengths belong to different orders of interference.

A concept frequently used to indicate how nearly identical two wavelengths must be to produce adjacent, same-order fringes is the "free spectral range" (FSR). This is just equal to one order of interference for a given interferometer arrangement.

Calculation of the free spectral range is illustrated in Example B.

Example B: Calculation of the Free Spectral Range
Given:	The mirror spacing of a Fabry-Perot interferometer is 10.5 cm. The space between the mirrors is a vacuum. The collimated beam of light is incident perpendicular to the mirror surfaces, and the order number N = 10,325.
Find:	The free spectral range.
Solution:	D l = (Equation 5) = cm = D l = 19.698 ´ 10–8 cm Since 10–8 cm = 1 angstrom (Å), D l = 19.698 Å

Fabry-Perot etalons are commonly used in conjunction with lasers in several ways. These include (1) use as a reflector, (2) studies of the mode characteristics of the laser, (3) obtaining single frequency operation of a laser, (4) mode selection, and (5) linewidth narrowing.

As a reflector element, the etalon makes use of the properties illustrated in Figure 4. Light that is not transmitted through the etalon is reflected. At positions where the transmission is low, the reflectivity of the etalon is high.

When the etalon is used as a reflecting element, it is commonly referred to as a resonant reflector. It is used mainly in high power solid lasers where the output mirror for the laser cavity must be able to sustain high powers without damage. The multi-layer dielectric coatings, which are commonly sapphire, are employed. The reflectivity is provided by the air-dielectric interface at the surface. Since this is relatively low, around 8% for a sapphire-air interface, the transmission maxima will be relatively low and broad. In order to provide high reflectivity, a number of elements (i.e., flat plates) may be stacked in series. The reflectivity R for M elements is given by Equation 6.

Note that the total number of surfaces is 2M. In this equation, n is the index of the refraction of the material between surfaces. Equation 6 is used in Example C to calculate the reflectivity of the resonant reflector.

Example C: Calculation of the Reflectivity of a Resonant Reflector
Given:	A certain resonant reflector consists of three plates of sapphire. The index of refraction of sapphire is 1.78.
Find:	The reflectivity of the resonant reflector.
	R =	(Equation 6)
Solution:	= = = R = 0.88, or 88%

Table 1 gives the reflectivity of a resonant reflector as a function of the number of plates.

Table 1. Reflectivity of Sapphire Resonant Reflector
(n = 1.78)

Table 1 shows that the reflectivity of the resonant reflector may be varied over a wide range, up to values approaching unity, by changing the number of plates in the stack. The elements are fabricated out of sapphire discs with the surfaces polished flat and parallel. The plates are held accurately in place by mechanical spacers.

Another type of Fabry-Perot device is the scanning mirror Fabry-Perot interferometer (SMFPI). In this Fabry-Perot interferometer, the optical path length between the mirrors is variable. For instance, one can mount the Fabry-Perot etalon in a cell in which the pressure of a gas (air or some other gas) can be varied, thereby changing the index of refraction and, consequently, the optical path length between the mirrors, or one can construct a spacer which can be varied. The following discussion focuses on the latter method, that is, a Fabry-Perot interferometer whose optical path length between mirrors is varied by changing the length of the spacer.

The various modes of a spherical-mirror cavity resonate at frequencies given by Equation 7.

(Note: This is the same resonance condition as that for laser cavities.)

The interferometer will have a high transmission for mode frequencies that satisfy the resonance condition as shown in Figure 4. The frequency difference between two adjacent resonance frequencies defines the free spectral range of the interferometer. In order for the free spectral range of the interferometer to be large enough to be useful, it is necessary to restrict the modes of this interferometer to a single transverse mode, that is, a single TEM mode. Then, the various longitudinal modes (different "q" values with m = n = o) determine the free spectral range to be c/2d (in frequency units), just as for the Fabry-Perot etalon. In practice, one finds that obtaining single transverse mode oscillation is very difficult, requiring precise optical alignment. Thus, further constraints or limitations on the general spherical mirror interferometer must be introduced before it becomes useful as an optical spectrum analyzer.

For practical application, mode-degenerate interferometers are generally used because optical alignments are not as critical as in general nondegenerate spherical mirror interferometers. (A mode-degenerate interferometer is a spherical mirror interferometer in which the frequency n _mnq of some of the transverse modes is the same as the frequency n _ooq of the axial or longitudinal modes.) An interferometer is mode-degenerate when—

Then the resonance frequency in Equation 7 becomes—

In general, the free spectral range of a mode-degenerate interferometer is c/2d. The spherical cavity for r = d/2 (l = 1) has the largest free spectral range c/2d. The spherical confocal cavity r = d (l = 2) has the largest finesse of any mode-degenerate interferometer and, for this reason, is the best known mode-degenerate interferometer. Thus, to obtain the desired finesse for analyzing laser radiation, a confocal interferometer is necessary. Figure 7 shows a typical confocal interferometer. It consists of two spherical mirrors, separated by a distance equal to the radius of curvature. The concave surfaces of the mirrors are coated with high reflectance dielectric films.

The mirrors are mounted against a piezoelectric spacer. By applying a potential difference of several hundred volts to the piezoelectric spacer, the separation of the mirrors can be varied by a few wavelengths.

The light transmitted by the interferometer is detected by a photodetector. The output signal of the photodetector is recorded as a function of the voltage applied to the piezoelectric spacer. The oscilloscope trace is, thus, a signal which is equivalent to the laser mode intensity versus optical frequency. A typical mode spectrum is shown in Figure 8.

As can be seen, there are six longitudinal modes in the laser output, and the amplitude of the modes is largest near the center of the mode spectrum.

To realize a calculated finesse F with a given aperture, the cavity mirrors must be perfectly spherical to within approximately l /2F across the aperture. This condition often requires the use of a restricting aperture if high spectral resolution is to be obtained, since the mirrors do not have this unusually high required spherical tolerance over a large area. Generally, there is an aperture outside the entrance mirror to limit the diameter of the incident beam, as shown in Figure 7.

To make the interferometer more convenient to use, a focusing lens is used to focus the radiation into the interferometer, thereby effectively increasing the aperture diameter. The focal point of the lens is located midway between the mirrors for maximum transmission.

An additional related application of Fabry-Perot etalons in conjunction with lasers is the production of single frequency outputs. This involves the insertion of an etalon within the laser cavity as shown in Figure 9. The mode structure of the laser cavity might be as shown in Figure 10. Suppose the transmission maxima of the Fabry-Perot etalon are located as shown in Figure 10. The laser will generally operate only at wavelengths which are simultaneously modes of the laser cavity and transmission maxima of the etalon since the gain of the system is highest at this wavelength. Therefore, the multi-mode nature of the laser is suppressed and only one mode will be present in the laser output. The frequency spacing is inversely proportional to the length of the cavity, so that the modes of the shorter etalon are more widely spaced, as shown. Typically, only one mode will lie within the fluorescent linewidth of the laser medium. The length of the laser cavity may have to be adjusted somewhat to ensure that the mode of the laser coincides with a transmission maximum of the etalon.

1. Assume that an argon laser illuminates a Fabry-Perot etalon with a spacing of 1.029 cm and with air (index of refraction = 1) between the mirrors. For the 0.5145 m m line of the argon laser, what is the value of N for the transmission maximum at 0° ?

2. A scanning Fabry-Perot interferometer (confocal) has a free spectral range of 33 GHz. Calculate the separation between the mirrors of the interferometer. What are the radii of curvature of the mirrors?

3. List the components of both the Fabry-Perot etalon and the scanning spherical mirror Fabry-Perot interferometer, and point out the major differences between these two variations.

4. List several applications of Fabry-Perot devices.

5. Show that Equation 2 can also be written in the form—

where D n is the frequency difference between adjacent longitudinal modes of a Fabry-Perot etalon.

6. Explain the meaning of finesse of a Fabry-Perot interferometer.

7. One Fabry-Perot interferometer has a mirror reflectivity of 75% while another one has a reflectivity of 98%. Which interferometer would be used to identify two closely spaced spectral lines?

8. A resonant reflector is required to have a reflectivity of more than 80%. The index of refraction of the plates is 1.5. How many plates are required?

9. A spherical confocal Fabry-Perot interferometer has a mirror spacing of 4 cm. Calculate the frequency difference between and .

10. A scanning Fabry-Perot interferometer having a mirror spacing of 5 cm is used to view the frequencies of a HeNe laser with an oscilloscope. Calculate the change in spacing of the mirrors that is required to display all frequencies present in the laser beam.

Before beginning the experiment, refer to the laser safety procedures and follow them. Four tasks will be performed in this experiment:

1. Set up the scanning Fabry-Perot interferometer and view the frequencies of the helium-neon laser.

2. Adjust the aperture so that the helium-neon laser is operating in a single transverse mode.

3. Use the interferometer to determine the longitudinal mode spacing of the helium-neon laser and the number of longitudinal modes which are lasing.

4. Adjust the intracavity aperture and etalon of an argon laser so that it is operating in a single longitudinal and single transverse mode.

The experimental arrangement for Task 1 is shown in Figure 11. Place the interferometer in the laser beam, and align the interferometer so that the laser beam is reflected more or less back on itself. With a relatively crude alignment, a spectrum will be obtained. To achieve maximum finesse, the alignment should be adjusted fairly carefully to ensure that the interferometer axis is close to the axis of the incident beam. This final adjustment can be accomplished by obtaining the best optical spectrum on the scope, a process which entails maximizing the amplitude of the displayed laser spectrum while at the same time minimizing the apparent width of individual spectral components.

The output of the oscilloscope’s ramp generator is used to drive the piezoelectric spacer in the interferometer. The ramp is synchronized with the x-axis sweep of the oscilloscope; thus, the horizontal distance in the scope picture is proportional to the optical frequency. The output of the photodetector is displayed directly on the vertical axis of the oscilloscope. (Light transmitted through the interferometer is a linear function of the interferometer transmission versus mirror separation.) A change in etalon spacing of ½ wavelength is sufficient to traverse one order of the etalon and, thus, display all the modes present in the laser output. The amplitude of the ramp voltage should be adjusted with the voltage divider so that the spectral scan will cover in excess of one free spectral range. This repetitive feature of the display will be used to calibrate the observed spectrum, since the free spectral range of the spectrum analyzer is known. (Note: The suggested scan rate of the scope is 2 msec/cm with line triggering. It is possible to scan at other rates up to about a kHz with no distortion in the response.) For ease of alignment, it is suggested that the scope have a vertical sensitivity of 0.005 volts/cm so that even a weak spectrum can be observed.

Figure 12 shows the output spectrum of a helium-neon laser operating simultaneously in two transverse modes. The uneven frequency spacing is a clue that the laser is operating in more than one transverse mode.

For Task 2, one gradually decreases the size of the aperture in the laser cavity until the mode spacing is the same for all modes, as shown in Figure 13.

To obtain the frequency difference between the longitudinal modes, one increases the interferometer until there are two spectral displays on the oscilloscope trace, as shown in Figure 14.

The two spectral displays are due to different orders of the interferometer. The frequency difference between the two spectral displays is equal to the free spectral range of the interferometer, which is given by manufacturers or can be calculated. For example, if the free spectral range of the interferometer used to obtain Figure 14 is 2 ´ 10⁹ Hz (2 gigahertz), then the frequency between point A and point B is 2 GHz. Thus, the horizontal calibration is 400 MHz/cm, since—

The horizontal frequency calibration is a linear function of the horizontal time scan; thus, if the scan time is doubled, the horizontal frequency calibration is also doubled. Therefore, by knowing the horizontal calibration, one can measure the frequency between the modes and the frequency width of one mode.

In Task 4, the intracavity aperture is adjusted to obtain a single transverse mode using the same method as in Task 2. Once a single transverse mode is obtained, the intracavity etalon is tilted to obtain a single longitudinal mode. The amount of tilt required will vary from laser to laser. Initially, the etalon is installed so that the laser beam is at normal incidence. While watching the spectral pattern on the scope, tilt the etalon until a single mode is obtained.