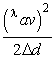| This version reflects the comments of the core participants as reviewed and incorporated in accordance with CORD's FIPSE-supported Curriculum Morphing Project. | |||||||||||||||||||||||||||||||||||||
MODULE 10-4 INTRODUCTION The Michelson interferometer is an optical instrument of high precision and versatility. It generally is used in investigations that involve small changes in optical path lengths. With the Michelson interferometer, one can produce circular and straight-line fringes of both monochromatic light and white light. One can use these fringes to make an accurate comparison of wavelengths, measure the refractive index of gases and transparent solids, and determine small changes in length quite precisely. The instrument can be used as a stable mode selecting resonator element in laser cavities as well. The Michelson interferometer is perhaps the best known and most basic in a family of interferometers which includes the Fabry-Perot interferometer, the Twyman-Green interferometer and the Mach-Zehnder interferometer. In this module, the student will learn how to use the Michelson interferometer. Modules that follow will treat, in turn, the use of the Fabry-Perot, Twyman-Green, and Mach-Zehnder interferometers. In learning how to use the Michelson interferometer, the student will accurately measure the wavelength of a chosen spectral line, the difference in wavelength between adjacent spectral lines, and coherence length of a mercury line and a HeNe laser. MODULE PREREQUISITES The student’s understanding of the principles involved in the operation and use of the Michelson interferometer will depend on mastery of previous material presented in the Laser Electro-Optics course. Therefore, before continuing with this module, the student should review the subject matter developed in Module 1-3, "Introduction to Laser Safety"; Module 5-3, "Wave Nature of Light"; Module 5-6, "Interference"; Module 6-5, "Mirrors and Etalons"; and Module 10-1, "Spectrometers." The usual mathematics of algebra and trigonometry will be sufficient to understand the mathematical formulas and derivations presented in this module.

Upon completion of this module, the student should be able to: 1. Identify the essential components of a Michelson interferometer by labeling these parts on an illustration provided and by writing an explanation of their function in the normal operation of the interferometer. 2. Adjust the Michelson interferometer for zero-path difference, produce both circular and straight-line fringes of monochromatic light, and produce white-light fringes according to instructions given in the Procedures section. 3. Determine the approximate wavelength of the sodium D-lines and the wavelength separation of the sodium D-lines according to given procedures. 4. Experimentally compare the coherence length of the intense 546.1-nm green light of
mercury and 632.8-nm red light from a HeNe laser. 
The Michelson interferometer operates on the principle of division of amplitude rather than on division of wavefront (see Module 5-6, "Interference"). According to this principle, the incident beam of light falls on a beam splitter which reflects roughly half of the intensity of the beam cross section or wavefront in one direction and transmits the other half of the intensity of the entire wavefront in another direction. The two beams which travel different optical paths are subsequently recombined in a common region where interference occurs and fringes are formed. The character of the fringes is directly related to the different optical path lengths traveled by the two beams and, therefore, is related to whatever causes a difference in the optical path lengths.
Optics of the Michelson Interferometer The important parts of a Michelson interferometer include a sturdy base, a diffusing glass, a beam splitter, a movable mirror with a micrometer screw for measuring distance of movement, a fixed mirror, and compensating glass. These parts are shown in a typical physical arrangement in Figure 1. The light source shown to the left can be a white light or spectral light source. It is not generally considered a part of the Michelson interferometer. Fig. 1
An accurately machined micrometer screw is attached to the movable mirror, permitting
the mirror to be moved toward or away from the beam splitter by a precisely determined
amount. The micrometer generally has about one inch of movement and usually can measure
mirror motion to within 0.002 mm. The two mirrors, beam splitters, and compensating glass
all are made of carefully annealed glass (e.g., borosilicate-crown). The mirrors are
front-coated with aluminum and protected with a The optical arrangement for the Michelson interferometer is shown schematically in Figure 2. Light from a broad spectrum source S, such as an incandescent bulb, passes through a diffusing glass DG (e.g., a ground glass plate), and strikes the beam splitter P. The beam splitter is a half-silvered glass plate (silvered on the back side) which reflects half of the light toward mirror M1 and transmits half of the light (but the entire cross section) toward mirror M2. Fig. 2
The compensating glass, CG, of identical composition and thickness to the beam splitter, is included so that each of the two beams (paths PM1PO and PM2PO in Figure 2) passes through the same thickness of glass. Note that otherwise the beam that travels along path PM1PO would pass through a thickness of glass three times while the beam that travels along the other path would pass through the same thickness of glass only once. The compensating glass is necessary if one wishes to produce white-light fringes; it would not be needed if one only worked with highly monochromatic light.
Condition for Interference—Monochromatic Light As we already know from Module 5-6, "Interference," if the optical path length PM1P is equal to the other optical path length, or if these two paths differ by a whole number of wavelengths l , the condition for constructive interference is met. Thus, bright fringes will be formed for that wavelength. This condition is written as Equation 1.
If, on the other hand, the two optical paths differ by an integral odd number of half wavelengths (p/2)l , where p = ±1, ±3, ±5, and so on, the condition for destructive interference is met and dark fringes will be formed in accordance with Equation 2.
If the two mirrors M1 and M2 are not aligned precisely perpendicular to one another, the path difference will depend on the particular region of mirror M1 (and the corresponding region of M2) which we are observing from the position O. The field of view, then, seen by looking at mirror M1 from position O will be made up of a series of alternately bright and dark fringes, nearly straight and parallel, similar to those produced by interference from a simple wedge. Such fringes are referred to as fringes of equal thickness, or straight-line fringes. If the path difference is near zero, the fringes will be broad and widely spaced in the field of view. On the other hand, if the path difference is on the order of 40 or 50 wavelengths (p = 40 or 50), the fringes will be narrow and closely spaced, so much so that they may be unresolvable with the naked eye. If the two mirrors are precisely aligned such that their planes are exactly perpendicular to one another, thus ensuring that path differences over different regions of the mirrors are constant, the fringe pattern will be seen by the observer at 0 to consist of a series of concentric rings. Each ring will correspond to a different angle of view measured from the perpendicular direction to the mirror M1, as illustrated in Figure 3. The fringes shown are called fringes of equal inclination. When the mirror M1 is moved so as to approach the condition for zero path difference, the fringe pattern will appear to collapse with all fringes moving toward the center, then disappearing. Fig. 3
Working with Two or More Wavelengths All of our discussion above has assumed that the light source was monochromatic, giving off light of only one wavelength. If there are two wavelengths, closely spaced as are the sodium D-lines, what then? As one might guess, there will be a different fringe system or set of fringes for each wavelength, and each wavelength will individually satisfy Equations 1 and 2 separately for bright and dark fringes, respectively. Most light sources produce many different wavelengths. In the case of a continuous white-light spectrum, for example, the many differently spaced fringe patterns representing the many different wavelengths will fall on top of one another and "wash" each other out, so that no fringes will be observed except near the center of the field of view. The fringes at the center will be distinct and white, while the nearby fringes will be made up of a "rainbow" of colors until washout occurs. It can be shown when there are only two wavelengths present in the incident light (each
of more or less equal intensity) that washouts will occur whenever the respective order
numbers for the two wavelengths differ by odd integral half-numbers such as
This equation will be used later to measure the wavelength difference of the two sodium D-lines. At that time the procedure will be clarified.
Coherence Length of Light Sources Laser light is highly coherent. Pure spectral line sources such as mercury and cadmium arcs are less coherent than laser light but much more coherent than white light. Coherence can be defined as the degree of stability of phase of a wave (light wave in our case) both in space and in time. By stability of phase in space we mean simply a fixed phase relationship between two separate points on the wavefront, while by stability in time we mean the constancy of phase within a single wave. We already have learned that the width of a spectral line is given by the width of the curve representing the line profile at half its maximum power—the so-called full-width-at-half-maximum (FWHM). If we present this spectral width in terms of frequency by D v, then it can be shown that the coherence length LC of a given light source is
The coherence length of a light source can be thought of simply as the length of an uninterrupted wave train of light. Thus, a highly coherent source that gives off light with no phase change will produce a long wave train and will be characterized by a long coherence length. A source that gives off short bursts of light, constantly interrupted by arbitrary and random phase changes, will produce short wave trains of light and, consequently, will be characterized as having a short coherence length. Lasers have coherence lengths on the order of tens of meters and longer, while white-light sources have a coherence length as short as one millionth (10–6) of a meter! A pure spectral line source such as the cadmium red line can have a coherence length as long as 40 centimeters, millions of times longer than the coherence length of white light, but considerably shorter than the coherence length of a stable laser. The Michelson interferometer measures coherence length of light sources directly. Since interference can never occur between overlapping wave trains whose phases have not remained constant and related—thus preventing the formation of fringes with an instrument such as the Michelson interferometer—we can get a rough estimate of the coherence length of light sources by measuring the largest difference in path length of the two mirrors over which we still observe fringe formation. Thus, if we call this difference 12 – 11 (equal to PM1P – PM2P), then Equation 4 becomes Equation 5:
Thus, one can experimentally determine the coherence length of a spectral source with a Michelson interferometer and check this result against the value of c/D v, provided the spectral line width D v is known. Or conversely, having measured the coherence length of, say, the mercury green line at 546.1 nanometers with the Michelson interferometer, one can quickly obtain information on the spectral width of this line by solving Equation 5 for the value D v.
Clearly, the wider the spectral line, the shorter the coherence length and the less coherent the light source. Likewise, the narrower the spectral line, the longer the coherence length and, thus, the more coherent the light source. 
1. Label the following parts of the Michelson interferometer shown in Figure 6:
Fig. 6
2. Explain, in your own words, the function of each part listed in Exercise 1. 3. Estimate the coherence length of white light (400-700 nm) with the help of Equation
4, LC = c/D v. Obtain D v for white light from the equation D
v = cD l /l 2, where D l will be taken to be one-half of the wavelength range of white light
4. The purpose of the compensating glass in Figure 1 and 2 is to make the optical paths PM1P and PM2P equal. However, this is not essential for the production of fringes with monochromatic light, although it is indispensable for the production of white-light fringes. Why? 5. The wavelength separation of two spectral lines whose average wavelength is 640 nm is 0.2 nm. If the lever arm between the micrometer screw and the movable mirror reduces the motion of the mirror to exactly one-fourth of that of the micrometer screw, how far apart on the micrometer screw will the successive washouts occur? 6. Explain how you would use a Michelson interferometer to make extremely accurate length measurements of about 0.01 mm or less. 7. How far must the movable mirror of a Michelson interferometer be moved in order that 3000 fringes of krypton-86 light (l = 606 nm) move across a line in the field of view? 8. Describe how you would use a Michelson interferometer to approximately determine the center wavelength of the nearly monochromatic light passed by an optical narrow-band pass filter. 9. If the movable mirror in the Michelson interferometer is moved through 0.233 mm, 792 fringes are seen moving past a reference mark in the field of view. What is the wavelength of the light? 10. A Michelson interferometer is used with a mercury discharge lamp. The yellow lines from the mercury light source have a wavelength of l 1 = 577.0 nm and l 2 = 579.0 nm. Using a 578.0-nm yellow filter between the light source and the diffusing glass (see Figure 1), it is observed that the interference pattern disappears and reappears periodically as one moves mirror M1 in Figure 2.
Michelson interferometer* White-light source (gooseneck lamp) Sodium lamp Mercury lamp Filter, 546.1 nm Hg line HeNe laser Microscope slide (2) Reading-telescope with scale Small mirror Micrometer Beam expander
*Several manufacturers of optical instruments make a so-called universal interferometer which permits modification of a common base to produce a Michelson, Fabry-Perot, and Twyman-Green type of interferometer. If one does not have interferometers already on hand, it is considered a wise investment to purchase a "universal" type interferometer. One then can use the same basic instrument to perform the experiments included in this module, as well as in Module 10-5, "Fabry-Perot Interferometer," and Module 10-6, "Twyman-Green Interferometer." 
Alignment of Michelson Interferometer Before beginning the alignment of the interferometer, you should make sure that you understand fully that ONE MUST NEVER TOUCH OR ATTEMPT TO CLEAN THE MIRRORS BY WIPING. And, as in the handling and operation of spectrometers, monochromators and spectrophotometers, ONE MUST NOT USE FORCE TO MOVE ANY PART OF THE INSTRUMENT. When in doubt, consult the instructor. The alignment of the Michelson interferometer can be accomplished in several simple, logical steps. First notice the small clip (pointer) that usually is provided as part of the diffusing glass screen and mount. (If none is available, simply tape a thin strip of black tape or make a black mark on the side of the diffusing glass [Figure 2] nearest the beam splitter.) This "pointer" will be used as a reference mark in aligning the interferometer for the production of fringes. 1. Turn on a sodium lamp source, waiting several minutes for the light to reach full intensity. Position the light source as shown in Figure 1 or Figure 2. From the observer’s position O, look towards mirror M1. You should see a yellow field of view, roughly the size of the diffusing glass. 2. Make the paths PM1 and PM2 equal to within a millimeter, using a white index card or small ruler. Now looking more carefully toward mirror M1, one should see three reflected images of the pointer in the field of view. (See Figure 4). Fig. 4
Mirror M2, the fixed mirror, is equipped with two screws on the back side that tilt the plane of the mirror. A slight adjustment of the mirror tilt screws will cause one of the three images to move. Align the mirrors by superimposing the movable image onto the right hand of the two remaining stationary images, as indicated in Figure 4. If you had carefully adjusted the tilt-screws and placed the two images in perfect coincidence, you should then be able to see fringes in the field of view, that is, looking into the interferometer toward mirror M1 from position 0. The fringes may, when first observed, appear rather closely spaced. See Figure 5a. While looking at the fringes, carefully adjust the screws on mirror M2 so that the fringes become circular with their common center lying in the center of your field of view. See Figure 5b. At this point, the two mirrors M1 and M2 should have their planes perpendicular to one another, that is, PM1 is perpendicular to PM2. Fig. 5
3. Normally before any adjustment of the interferometer takes place, the two path lengths PM1 and PM2 are very likely unequal. Moving mirror M1 back and forth along PM1 will change the difference in path lengths and, in fact, permit us to reduce the difference to very near zero. As we mentioned above, when mirror M1 is moved so as to approach equal path lengths, the fringes move inward toward the center, collapsing and eventually disappearing altogether. See Figure 5c. Carefully turn the micrometer screw in a direction that causes the fringes to move toward the center and disappear. Continue until the field of view is entirely dark as in Figure 5d. (Note: This condition may be difficult to achieve since air currents or small table vibrations constantly cause small random changes in the path length. Nevertheless, one should approach the "dark-field" condition as closely as possible.) 4. Replace the sodium lamp with a white-light source such as a gooseneck lamp. With the interferometer still adjusted for zero-path difference as in Step 3, look into the interferometer for the white-light fringes. If you do not see the white center with the rainbow-hued fringes nearby, slowly and carefully move the micrometer screw back and forth. Frequently, a keen eye and a steady hand are required to locate the white-light fringes. The four steps outlined above are generally sufficient to permit one to align a Michelson interferometer to produce straight-line fringes of a given color or white-light fringes near zero-path difference.
Measurement of the Approximate Wavelength Adjust the Michelson interferometer, with the sodium lamp warmed up and in place, to produce circular fringes in the field of view as described above. Turn the micrometer screw a quarter-turn in the direction of decreasing reading. This is done to avoid backlash since all readings will be taken with the screw moving in the same direction (decreasing readings). Record the reading of the micrometer. Count the number of fringes that appear (or disappear) in the center of the field of view, as the micrometer screw is turned slowly in the direction of decreasing reading. After counting 50 fringes, record the micrometer reading again. Continue this process through 250 fringes, recording the micrometer reading after each set of 50 fringes has been counted. As you will experience, this procedure requires a certain amount of technique (and patience), since the slightest movement of the screw will gain or lose fringes. When you stop turning the screw at the end of 50 fringes, be very careful to keep it rigid. In most interferometers, the mirror is moved by a lever arm that reduces its motion to
some fraction (say Correct the micrometer reading for the proper reduction ratio. Estimate the uncertainty in the corrected micrometer reading for 50 fringes by examining the differences in the five different readings of the 50 fringes sets. Calculate the average wavelength of the sodium light (sodium D-lines) and its uncertainty. Use Equation 1 to obtain the average wavelength, pl = PM1P – (P, CG, M2 CG, P) or in present terms, 50l = 2(do – d50). Both do and d50 are the micrometer readings corrected for the proper reduction ratio.
Measurement of the Wavelength Separation With the sodium lamp in place, set the micrometer screw somewhere between two-thirds and three-fourths of its total movement (for example, between 15 and 20 mm for a 25-mm micrometer screw). As the micrometer is turned toward smaller readings, the observer, looking toward mirror M1 from position O (Figure 2), should notice that the fringes periodically becomes less distinct and nearly washed out (disappear). Measure the position of as many of these successive washouts as possible (about every 1000 fringes) ensuring that the micrometer screw is moved always in the direction of smaller reading for each washout position. Repeat this procedure several times. Calculate the average value for the washout distance, D d. With this value and the average value for l (sodium light) determined in the preceding experiment, calculate the wavelength separation between the two sodium D-lines from Equation 3—namely,
Here (l av)2 has been used as a reasonable approximation for l 1l 2 in Equation 3. Check your result for D l against the difference obtained from a handbook where (l 2 – l 1) is given as 589.5923 nm – 588.9953 nm = 0.5970 nm. Determine if the variation between your result and the handbook’s result is reasonable, considering the uncertainty of your values of l av and D d.
Measurement of Coherence Length With the mercury light source in place and turned on, wait until it has reached its full intensity. Place a 546.1-nm Hg line filter between the mercury light source and the diffusing glass. Adjust the Michelson interferometer for green-line fringes. Turn the micrometer screw on either side of the position that approximately marks equal path lengths, until the fringes are seen to disappear. Locate the midpoint of this motion. Read the micrometer screw and call this reading R1. The student should readily see that this reading sets an index that indicates the equality of paths PM1 and PM2. Now move mirror M1 away from the beam splitter P and record the micrometer reading at the position where the green-line fringes just disappear. Call this reading R2. Now move mirror M1 back to micrometer reading R1 (check to make sure green-line fringes are again clearly visible) and continue moving mirror M1 toward the beam splitter until green-line fringes again disappear. Call this reading R2'. The student should see that (R2 – R1) and (R1 – R2') are roughly equal and that twice this difference equals the coherence length of the mercury green line. Check this value of the coherence length Lc = 2(R2 – R1) by obtaining D v, the FWHM for the 546.1-nm line, and calculating the coherence length from Equation 5, LC = c/D v. Do not forget the correct (R2 – R1) for the reduction ratio. The FWHM for the 546.1 Hg line can be taken as 2.17 Å or 2.18 ´ 1011 hertz. Remove the mercury filter and replace the mercury source with a HeNe laser. Position a beam expander between the laser and diffusing glass. Do not turn the laser on at this point. Do not remove the diffusing glass. OBSERVE ALL SAFETY PRECAUTIONS FOR USE OF HeNe LASERS IN THE LABORATORY. Set the optical path lengths PM1 and PM2 roughly equal with an index card. Now turn the HeNe laser on. DO NOT LOOK toward mirror M1 from position O. Instead, about a meter or so from the beam splitter, along the line M1 PO, place a white cardboard (a screen) on which the fringes can be observed indirectly. The room lighting may have to be dimmed somewhat. Red fringes now should be seen without difficulty. Move the micrometer screw along its entire range. The fringes will remain with little change. The student will conclude that the difference in path length (R2 – R1) cannot be made sufficiently large with this Michelson interferometer to reach the position where the red fringes disappear. This should come as no surprise since, in the discussion on coherence length, it was pointed out that for most lasers the coherence length easily exceeds meters in length. Thus, with a Michelson interferometer whose total traverse of the micrometer screw is on the order of 25 millimeters, fringes of HeNe laser light can easily be produced, but the coherence length cannot be measured. One can only conclude that it is greater than 2 ´ 25 mm. (We know that it is much greater.) 
Born and Wolf. Principles of Optics. 4th ed. New York: Pergamon Press, 1970. Cagnet, M., Francon, M., Thrierr, J.C. Atlas of Optical Phenomena. New York: Springer-Verlag, Inc., 1962. Francon, M. Optical Interferometry. New York: Academic Press, Inc., 1966. Hecht and Zajac. Optics. New York: Addison-Wesley Publ., Co., 1974. Jenkins and White. Fundamentals of Optics. 3rd ed. New York: McGraw Hill. Meyer-Arendt, J.R. Introduction to Classical and Modern Optics. Englewood Cliffs, NJ: Prentice Hall, 1972. Kingslake, R., ed. Applied Optics and Optical Engineering. Vol. IV. See section on "Interferometers" by Baird, K.M. and Hanes, G.R., Part I, pp. 309-361. New York: Academic Press, Inc., 1967. Palmer, C.H. Optics Experiments and Demonstrations. Baltimore, MD: The John Hopkins Press, 1962. Sears, Zemansky, and Young. University Physics. 5th ed. New York: Addison-Wesley Publ., Co., 1976. Steel, W.H. Interferometry. University Press, 1976. Strong, Y. Concepts of Classical Optics. W.H. Freeman and Co., 1958. --------------------------------------------------------------
|
|||||||||||||||||||||||||||||||||||||
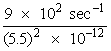 = 0.297 ´
1014 Hz
= 0.297 ´
1014 Hz