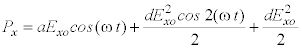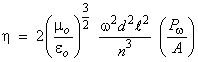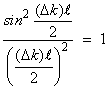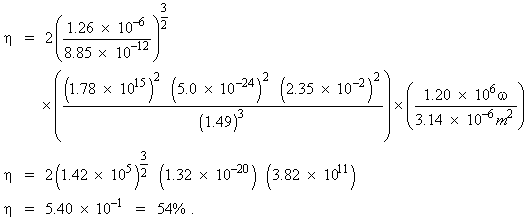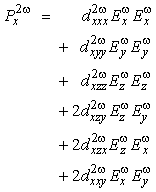MODULE 6-11
NONLINEAR MATERIALS
General Comments of Leno Pedroitti
ã Copyright 1988 by The Center for Occupational Research and Development
All rights reserved. No part of this book may be reproduced in any form or by any means without permission in writing from the publisher.
The Center for Occupational Research and Development
601 C Lake Air Drive
Waco, Texas 76710
Printed in the U.S.A.
ISBN 1-55502-024-0
(1) Nonlinear optical materials are materials in which the intensity of light input, including its frequency, is not related to the intensity of light output by a simple proportionality constant. Because of this nonlinear behavior, an intense light beam propagating through a nonlinear optical material will produce new effects that can’t be seen with weak light beams. For example, an intense light beam propagating through a nonlinear material can generate, in addition, harmonics or overtones of the original light frequency. This means that the red beam from a ruby laser can create an ultraviolet beam as it passes through the nonlinear optical material, while itself still propagating as a red beam.
(2) The interaction of intense light beams with nonlinear materials has opened a large field of potential applications in optical communication systems, where many well-known radio-frequency techniques such as mixing, heterodyning, and modulation now can be transferred to the domain of optical frequencies. For these reasons, nonlinear materials play an ever-increasing role in laser applications.
(3) This module will familiarize you with the fundamental physical ideas that underlie some of the more commonly encountered nonlinear phenomena and how these phenomena depend on the properties of the nonlinear materials. The experiment at the end of this module will give you practical experience in using a nonlinear material to generate the visible second harmonic of the invisible 1.06-mm Nd:YAG laser wavelength.
(4) For a better understanding of the ideas in this niodule, you should have knowledge of algebra and some trigonometry. Before beginning the experiment at the end of this module, be sure to review laser safety.

(5) When you complete this module, you should be able to do the following:
-
Describe the nonlinear behavior of a system by describing its linear and nonlinear behavior with appropriate equations.
-
Explain second harmonic generation of light with the aid of the induced charge polarization.
-
Discuss in general terms the need for phase matching in second harmonic light generation.
-
Describe two experimental techniques used for phase matching.
-
List the various materials and experimental parameters that determine the efficiency of second harmonic generation through the use of the correct mathematical equations.
-
Differentiate between passive and active nonlinear materials.
-
List and rate the importance of some of the more common nonlinear materials.
-
Define the field-dependent nonlinear index and its implications.
-
Produce the second harmonic (0.53 mm) of the 1.06-mm radiation from a Nd:YAG laser using a crystal of KDP or ADP.
-
Knowing the type of SHG crystal, its size and operating parameters, estimate the theoretical conversion efficiency.
DISCUSSION
(6) Our objective is to develop a familiarity with the behavior and application of nonlinear materials. We’ll do this by first describing the behavior of a linear system or material. Next, we’ll look at its nonlinear behavior and discuss the internal properties of the material that make it behave in a nonlinear fashion. Finally, we’ll describe in a very elementary fashion the fundamental physical idea behind one of the more common nonlinear effects and how this effect depends on the properties of the nonlinear material. We conclude this section with a brief discussion of the more common nonlinear materials.
(7) Let’s start then with a brief discussion of linear materials and linear effects. It is a fact that our everyday experiences tell us that we live in an essentially linear world. When you first encounter the mathematical expressions of elementary physical laws, you may be tempted to conclude that nature is linear. For example, you learn that gas pressure in a container will double if the temperature of the gas is doubled; or that when a given force on a spring produces a stretching of the spring of one centimeter, then doubling the force will produce a stretching of exactly two centimeters. The example of the stretching spring is shown schematically in Figure 1.
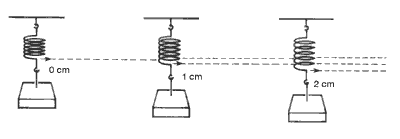
Fig. 1
Linear displacement of a spring
(8) From these and other examples you might conclude that the response to small disturbances in all physical systems follows a linear law. Doubling the cause doubles the effect, tripling the cause triples the effect, and so on.
(9) Consider once more a linear spring. The mathematical expression relating the force F on the spring to the stretching of the spring in the x-direction is
|
F = kx
|
Equation 1
|
where the proportionality constant k is the spring constant.
(10) In practice, as long as the stretching of the spring is small compared to the total length of the spring, the force can be calculated with Equation 1. However, when the distance through which the spring is stretched exceeds a certain limit, the magnitude of the force F no longer is related to the distance x in a simple linear manner. Then it’s more accurately expressed by the nonlinear relation.
|
F = kx
+ k'x2 + k"x3
+ k"'x4 + . . .
|
Equation 2
|
where k', k", k"' are higher order constants and are much smaller than the constant k.
(11) The magnitude of the force as a function of the distance the spring is stretched is shown in Figure 2, where the linear as well as the nonlinear behavior of the spring is illustrated.
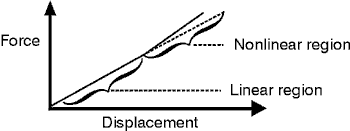
Fig. 2
Linear and nonlinear behavior at a stretched spring
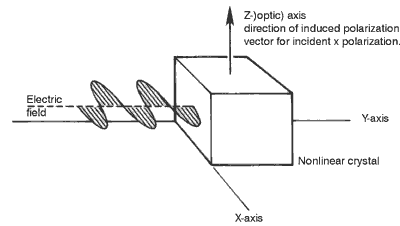
(12) Now we’ve stated what we mean by "linear" and "nonlinear" behavior of a system (the spring). Let’s next discuss the nonlinear behavior of certain materials when intense light beams propagate through them. These light beams are of course electromagnetic waves that are made up of an electric field and a magnetic field. Both fields are locked in step at right angles to each other and oscillate together at the frequency of the light, as you have already learned.
(13) Consider what happens when such an oscillating field interacts with an atom, which you can think of as a positively charged nucleus surrounded by shells of electrons. The electrons in the outermost shell are more loosely bound, and their radial displacements are governed by the same force equation that describes the stretching of a spring. These outermost electrons can redistribute themselves in step with the electric field. In this way the atom becomes charge-polarized. This means that positive and negative parts separate slightly to form a small electric dipole with a so-called dipole moment pointing in the direction of the impressed field. The dipole moment is the magnitude of the displaced charge times the distance between the positive nucleus and the center of the displaced electron shell. (Note that when not displaced, the center of a spherical election shell is, of course, at the same location as the positive nucleus.)
(14) The number of electric dipoles per unit volume multiplied by the dipole moment of one atom gives the induced macroscopic charge polarization of the material. (Don’t confuse this charge polarization induced by the electric field of the light beam with the polarization of a light beam with a polarizing filter.)
(15) In any given material, the magnitude of the induced charge polarization depends on the magnitude the applied electric field E. Specifically, we can express the charge polarization P in a series of powers of E and write
|
P = aE
+ dE2 + d'E3
+ . . .
|
Equation 3
|
| where: | a | = | Polarizability coefficient of the material |
| d, d', etc. | = | Higher-order nonlinear optical coefficients that are much less than a |
The similarity between Equation 3 and Equation 2 should be clear.
(16) The electrons in the outermost shell not only are subject to the pulling of the applied external field, but also are subjected to the pull of the internal field due to the positive nucleus. The magnitude of this internal electric field is enormously large, somewhere in the neighborhood of 109 volts/cm. For comparison, the electric field of sunlight at the surface of the earth is only about 10 volts/cm. It turns out that, when the applied electric field is many orders of magnitude less than the atom’s internal electric field—which is always the case for ordinary light sources—the linear approximation P = aE of Equation 3 is very accurate.
(17) With the development of the laser in 1960 we were able to build light sources capable of producing optical electric fields of 106 to 107 volts/cm. When some optical materials are irradiated by such intense fields, the contribution to the charge polarization by the higher-order terms in Equation 3 no longer can be neglected.
(18) Let’s see what happens when we use only the first two terms in Equation 3. For simplicity, let’s also assume that the electric field points in the x-direction. Then the total induced charge polarization in the x-direction is
|
Px
= aEx + dE2x
|
Equation 4
|
(19) For plane polarized light of frequency f and amplitude Exo, the electric field at some given point in an optical material is described by
|
Ex
= Exo cos(2p ft)
= Exo cos (w t)
|
Equation 5
|
where w º 2pf º the "angular frequency" in rad/sec
and the induced charge polarization is
|
Px
= aExo cos (w t) + dE2xo cos2
(w t)
|
Equation 6
|
Using the trigonometric identity
|
|
Equation 7
|
Equation 6 can be written as:
|
or Px = Px (w) + Px(2w) + constant term (DC) |
Equation 8
|
(20) An inspection of the above equation reveals that the first term Px(w) is a charge polarization of angular frequency w. The second term Px(2w) is a charge polarization of angular frequency 2w, twice the fundamental frequency w. Finally, the third term has no frequency dependence whatsoever. It provides a "DC" charge polarization. The three charge polarization terms are shown in Figure 3. Equation 8 then tells us that a rapidly oscillating electric field in the neighborhood of 1014 to 1015 Hz (optical frequencies) will induce two types of oscillating charge polarization; one of frequency w and another of frequency 2w. The material consists, then, of a collection of oscillating dipoles that absorb and reradiate light waves. The total energy in the beam of light is not significantly altered.
(21) One effect of the induced charge polarization and subsequent reradiation is a decrease in the speed of the light in the medium. The decrease in speed is reflected in the increased value of the index of refraction n, which is given by the ratio of the speed of light in vacuum c divided by the speed of light in the medium v, that is, Equation 9,
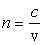 |
Equation 9
|
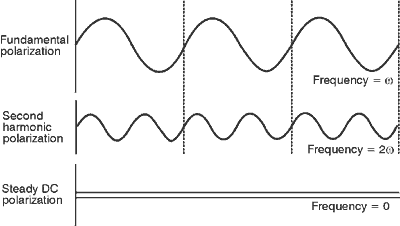
Fig. 3
Frequency associated with charge-polarization terms
(22) Another effect, predicted by Equation 8, is the reradiation of energy at the frequency 2w, twice the frequency of the incident radiation. This doubling of frequency is known as "second harmonic generation" (SHG) or "frequency doubling."
(23) Frequency doubling was observed for the first time in 1961 by Professor Peter Franken and some graduate students at the University of Michigan. They irradiated a quartz crystal with the beam from a ruby laser that operated at 694.3 nm. A very small amount of the light striking the crystal was converted to light with a wavelength of 347.2 nm. This wavelength lies in the ultraviolet region of the spectrum and is of course exactly half the wavelength and twice the frequency of the incident laser light.
(24) The details of this famous experiment are shown in Figure 4. As you might expect, this experiment initiated a search for materials in which this effect occurs strongly. As a result, the experiment has been duplicated many times with a host of different nonlinear materials.
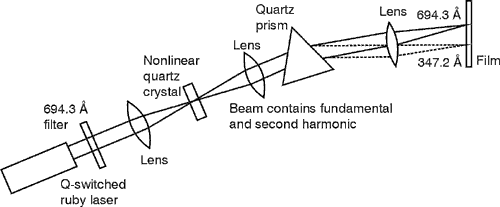
Fig. 4
Experimental arrangement for second harmonic generation
(25) What are the properties of a crystal that are responsible for efficient SHG? To answer this question let’s first note that, whatever these properties may be, they manifest themselves in the expansion coefficient d of the second-order term in Equation 3.
(26) To find out how d is governed by the internal properties of the crystal, we need to examine the oscillatory motion of the dipoles. This is best done by adding the three curves in Figure 3. The resultant charge polarization is shown in Figure 5, along with the applied electric field.
(27) The curve for the total polarization shows mainly the contributions of the fundamental polarization and steady DC polarization terms. The contribution of the second harmonic term would cause a slight change in the slopes of the rise and fall of the total polarization, but not in the location of the maximum, zero, and minimum points. So its effect has not been shown in the lower curve in Figure 5.
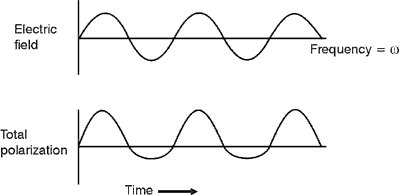
Fig. 5
Impressed electric field and resulting total polarization
(28) It’s clear from Figure 5 that the individual dipoles, whose oscillatory motions lead to the charge polarization, do not faithfully reproduce the sinusoidal electric field. Note especially that the total polarization is asymmetric in the upward direction. This is because the outer electrons of the atoms in a crystal are more easily pushed in one direction than in the opposite direction.
(29) Figure 5 shows that an intense electric field in the up-direction is more effective in polarizing the medium than the same field in the down-direction. Such a situation can occur only in a crystal with no internal symmetry. Only about 10% of the crystals found in nature fall in this category.
(30) The distorted charge polarization wave produced by the intense radiation field travels at the same speed as the incident light wave. This light, which is reradiated by the oscillating dipoles, contains, as we saw above, two discrete frequencies w and 2w. Since the refractive index for the light of frequency 2w is usually larger than it is for light of frequency w, the speed of the component with frequency 2w will be just a bit slower than the component with frequency w, in accordance with Equation 9.
(31) The difference in propagation speed between the fundamental frequency and the second harmonic frequency means that the second harmonic light radiated from one part of the crystal, say P(1), will not be in phase with the second harmonic light radiated from another part of the crystal P(2). As a result, the two waves from P(1) and P(2) will interfere destructively at some point P(3). The distance that it takes for a second harmonic charge polarization wave and its radiated light to get 180° out of phase is called the "coherence length." This distance is usually on the order of 10 µm. If the crystal length happens to be equal to an odd multiple of the coherence length, virtually no second harmonic radiation will emerge from the crystal.
(32) This problem of destructive interference can be overcome by making use of the double-refraction birefringence exhibited by certain crystals. It turns out that in such crystals the velocity of light depends on the direction of polarization of the electric field, the propagation direction, and the wavelength.
(33) For example, the speed of light in the nonlinear material potassium dihydrogen phosphate (KDP) for the horizontally and perpendicularly polarized electric field components is shown in Figure 6. As you can see, the ordinary fundamental that we have taken to be the light from a ruby laser at 694.3 nm, polarized perpendicular to the plane of the page, travels at exactly the same speed as the extraordinary second harmonic light at 347.2 nm, when both light waves propagate in a direction that’s inclined 50° to the optic axis of the crystal. The optic axis of a doubly refracting crystal is that direction along which the ordinary and extraordinary waves of the same frequency propagate at the same speed.
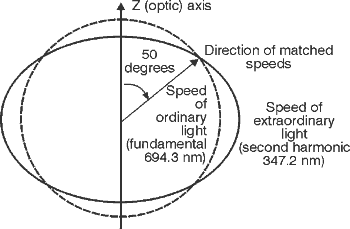
Fig. 6
Velocities of ordinary and extraordinary light in KDP
(34) When the direction of propagation of the fundamental is chosen so that the index of refraction of the fundamental and second harmonic are the same, both waves will stay in phase. The crystal then is said to be phase-matched or "index-matched." The second harmonic wave produced at any given point in the beam now will interfere constructively with the second harmonic wave produced further "downstream" in the beam. As we will see later, when the light travels along the index-matching direction, the efficiency for SHG can be improved very significantly.
(35) Phase-matching also can be achieved in some crystals by varying their temperature. The reason is that the extraordinary index is in general more temperature-dependent than the ordinary index. So by varying the temperature you can adjust the birefringence of the crystal until phase matching is obtained. The exact temperature for phase matching depends on the exact chemical composition of the crystal. This effect was discovered by accident when it was noted that different crystals of lithium niobate required different phase-matching temperatures under otherwise similar experimental conditions.
(36) For the niobates in which the phase-matching is achieved by controlling the temperature, the apparatus shown in Figure 7 is used to determine the phase-matching temperature for any given crystal. A laser such as Nd:YAG operating at 1.06 mm is used to illuminate the crystal. The intensity of the second harmonic is monitored and displayed with a pen recorder as the temperature of the crystal is tuned through the phase-matching temperature.
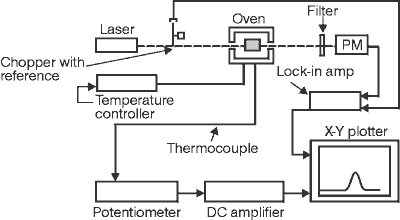
Fig. 7
Apparatus for determining phase-matching temperature in
birefrigent crystals
(37) It turns out that a perfect crystal should give a plot of second harmonic power versus temperature that has a [(sin x) / x]2 dependence. However, because of slightly varying chemical compositions at different sites of the crystal, different portions of the crystal will phase-match at slightly different temperatures. The result is a broadening of the central peak and a reduction in height. Furthermore, the side lobes are obscured. A typical curve of second harmonic power versus temperature for an ideal crystal and a nonideal crystal is shown in Figure 8.
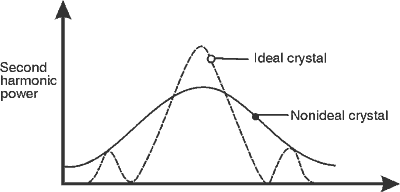
Fig. 8
Second harmonic power output versus temperature
(38) The conversion efficiency, h SHG defined as the ratio of the emerging second harmonic power P(2w) to the incident power P(w) is one of the most useful measures of the performance of a nonlinear crystal. It is given by
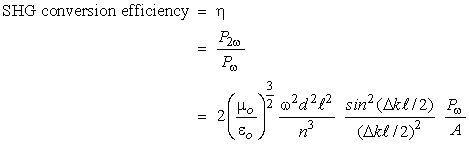 |
Equation 10
|
|
| where: | Dk | = | k2w – 2kw |
| k | = | 2p/l | |
| eo and mo | = | Permittivity and the magnetic permeability of free space, respectively | |
| n | = | Index of refraction | |
| w | = | Angular frequency of the incident light | |
| d | = | Second-order coefficient | |
 |
= | Length of the crystal | |
| A | = | Beam area |
(39) The factor Dk represents the amount of phase mismatch between the second harmonic wavefronts generated at different points in the crystal. If Dk is zero (proper phase-matching) then the "interference" term,
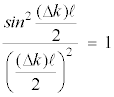
reaches a maximum value that in turn maximizes the efficiency of the SHG process. Note that the "interference" term is squared, making the power converted into the second harmonic very sensitive to phase mismatches.
(40) The efficiency of second harmonic
generation is directly proportional to the intensity  of the incident fundamental radiation. This is why second harmonic generation
often is done in an intracavity configuration since the higher power of
the fundamental produces much higher intensities than are achievable in
external convertors.
of the incident fundamental radiation. This is why second harmonic generation
often is done in an intracavity configuration since the higher power of
the fundamental produces much higher intensities than are achievable in
external convertors.