MODULE 6-8
LENSES
—————————————————————————————————
©Copyright 1987 by The Center for Occupational Research and Development
All rights reserved. No part of this book may be reproduced in any form or by any means without permission in writing from the publisher.
The Center for Occupational Research and Development
601 C Lake Air Drive
Waco, Texas 76710
Printed in the U.S.A.
ISBN 1-55502-024-0
—————————————————————————————————
(1) People have understood and used simple lenses for hundreds of years. References to the use of a magnifying glass and telescopes occur in writings from the eleventh century. The Romans named the "lens" because they saw a resemblance between this optical component and the Rat round seeds of the lentil plant.
(2) An optical lens is a carefully ground or molded piece of glass, plastic, or other transparent material that has opposite surfaces. Either or both of these surfaces are curved. Lenses bend light rays so that they diverge or converge to form an image. Lenses are essential components for telescopes, microscopes, binoculars, eyeglasses, cameras, projectors and many other items of everyday use that employ optical components.
(3) This module will acquaint you with functional classes of lenses and will describe specific configurations and applications of several commonly used lenses.
(4) Before you begin this module, you should have studied the principles of refraction and ray tracing optical components.

(5) When you complete this module, you should be able to do the following.
1. Explain these terms, concepts or instruments. You should convey the same meaning as given in the text.
a. Converging lens
b. Diverging lens
c. Power of a lens
d. Focal length of a lens
e. Lens systems
f. Collimation
g. Spherical aberration
h. Chromatic aberration
i. Coma
j. Astigmatism
k. Distortion
l. Field curvature
m. AR coatings
n. Damage threshold
2. From a cross-sectional diagram, identify the following lenses:
a. Biconvex
b. Plano-convex
c. Convex meniscus
d. Biconcave
e. Plano-concave
f. Aspherical
g. Cylindrical
h. Fresnel
3. Experimentally determine the focal length of a concave lens and a convex lens.
4. Construct a simple beam expander using two positive lenses.
5. Illustrate spherical aberration in lenses and a way to read it.
6. Write an explanation of the effects of spherical aberration on a camera.
DISCUSSION
(6) Lenses are used to change the direction of rays of light. Figure 1 shows how lenses form images by refraction. The effect of a lens on light is embodied in Snell’s law—the law of refraction. This law states that, in passing from a rarer medium into a denser one, light is refracted toward the normal. In passing from a denser to a rarer medium, light is refracted away from the normal. The degree of bending or refracting is in accordance with the equation:
n1 sin q = n2 sin q 2 |
Equation 1 |
| where: | n1 and n2
= Indices of the two media q 1 and q 2 = Angles of incidence and refraction respectively |
Fig. 1
Image formation by a simple lens
(7) Let’s build a mental picture of a lens that has a number of straight-line prisms as shown in Figure 2a. When the number of prisms is very large, as shown in Figure 2b, the multiple straight-line segments begin to approach the curved surface of a lens. Figure 2 illustrates the law of refraction.
(8) There are many types of lenses. But they all can be classified into two general types according to the effect they have on a parallel beam of light. The two types are converging and diverging lenses.
1. Converging lenses also are called "positive," "plus," or "convex" lenses. They are thicker in the middle than at the edges. As shown in Figure 3, they cause both parallel rays of light and diverging rays of light on the opposite side of the lens.
Fig. 2
Evolution of lenses from basic prism pairs
Fig. 3
Effect of positive (converging) lenses on plane and diverging spherical wave fronts
2. Diverging lenses are known as "negative," "minus," or "concave" lenses. They are thinner in the middle than at the edges. Figure 4 shows us that a diverging lens causes parallel rays of light to diverge or spread in opposite directions on the other side of the lens. If rays initially are diverging toward such a lens, they will be made to diverge even more strongly after they pass through the lens. (See Figure 4b.)
Fig. 4
Effect of negative (diverging) lenses on plane and diverging spherical wave fronts
(9) All lenses can be classified as converging or diverging. But further subdivisions of these two basic types can be made according to the curvature of the lens surfaces and the power of the lens. Spherical lenses are lenses whose surfaces are spherical in shape. Spherical lenses can be classified into the six sub-types shown in Figure 5. The biconvex lens—"i"—is used the most of these six.
Fig. 5
Types of simple spherical lenses
(10) You should have studied the definition of focal points and focal lengths for simple lenses already. It would be a good idea for you to review that definition now. Here we’ll briefly restate the essentials.
(11) The focal length of a "thin lens" is the distance the focal point is removed from the vertical centerline of the lens. The focal point F’ (Figure 6) of a positive lens is that point where parallel rays of light from the left are brought together. The focal point F on the left side of the positive lens is that point to which parallel rays, incident on the lens from right-to-left, would converge.
Fig. 6
Parallel rays of light brought to a focus by a positive thin lens
(12) The focal point F (Figure 7) of a negative lens is the point where parallel rays of light seem to originate. The focal point F
' on the right side of the lens is the point from which light would seem to diverge, after passing through the lens, if it were incident on the lens from right-to-left.Fig. 7
Parallel rays of light incident on a negative thin lens diverge
as if coming from a point F on the left.
(13) Focal lengths are shown as f
' and f in Figures 6 and 7. For a thin lens, f and f ' are equal.(14) The power of a lens is the reciprocal of its focal length in meters. The power of a lens is a measure of its ability to converge or diverge light rays. For example, the higher the positive power, the more converging the lens. The unit of power is the "diopter." Diopter usually is designated as D. One diopter is the power of a lens with a focal length of one meter. So a converging lens with a focal length of 20 cm (0.2 m) has a power of 1/0.2 m = 5 D. Note that a lens that causes light to converge has a positive power, and a lens that causes light to diverge has a negative power. As an example, a diverging lens with a focal length of –25 cm (–0.25 m) has a power of 1/–0.25 m = –4 D.
(15) A second type of lens whose basic shape differs from the spherical lens is the cylindrical lens. Cylindrical lenses are so named because their surfaces are cylindrical in shape.
(16) Figure 8 shows how a cylindrical lens focuses incident parallel light onto a focal line rather than onto a focal point as in the spherical lens. Cylindrical lenses are used in optical data processing and in other applications where we don’t need the formation of an image in true dimensions. Cylindrical lenses sometimes are used also to image the rectangular mode shape of a pulsed nitrogen laser into a straight line. For example, they would be used in pumping an organic dye laser cell.
Fig. 8
Cylindrical lens
(17) A third type of lens that’s classified by its shape is the Fresnel lens. The Fresnel lens looks different from the spherical and cylindrical lenses. A Fresnel lens is a disk-shaped optical component with almost no thickness. It focuses and collimates light by means of a series of concentric (like a bull’s-eye) grooves. Curvature of the grooves causes refraction of the incident beam, approximating that of a conventionally shaped lens as shown in Figure 9.
Fig. 9
Comparison of the shape of a normal lens to that of a Fresnel lens
(18) Figure 10 shows Fresnel lenses used as a collimator and as a collector. You can understand the effect of a Fresnel lens on light by again constructing the lens from many small prisms. The difference between conventional and Fresnel lenses is that the Fresnel lens has prisms laid out in a circular pattern in the same plane instead of being stacked together to form a regular lens.
Fig. 10
Action of Fresnel lens
(19) Fresnel lenses often are constructed of rigid acrylic. They are available in positive, negative, and cylindrical configurations. Fresnel lenses are durable, lightweight (1/10 the weight of equivalent conventional elements) and comparatively inexpensive. Their optical quality is relatively poor. Fresnel lenses typically are used as field lenses, condensers and magnifiers, in viewers, microfilm readers, copiers, compact optical systems, and in wide-angle visual simulators. A most frequent application is in traffic lights.
(20) Various types of lenses are used in different applications. The biconvex lens is the most common and most important lens. Since this is the type of lens in the eye for vision, we will take a brief look at its characteristics.
(21) The lens of the eye is made of a transparent, flexible medium with attached muscle so that the lens can be made to change its shape (and consequently its focal length). The power of the lens thus is adjusted to focus objects located at different distances from the eye onto the back of the eye where the images eventually are interpreted by the brain. This changing of power is called accommodation of the eye. It’s shown in Figure 11.
Fig. 11
Accommodation of the eye
(22) When the eye muscle is relaxed, the lens is shaped so that light coming from an object at infinity is focused onto the back of the eye as shown in Figure 11a. When an object closer to the eye is viewed, the eye must accommodate and thicken the lens so that the image point again is placed on the back of the eye, as shown in Figures 11b and 11c. Accommodation in a normal eye lets us clearly see objects located anywhere from infinity to ten inches from the eye.
(23) Next, we will examine several applications of the simple positive lens. A single lens forms the basis for a simple magnifier as well as a basic part of the microscope and telescope. So, first we will discuss the essential optics of the magnifier. Then we will examine the optics of a searchlight, essentially a scheme for "throwing" a collimated beam of light a long way. Following this we’ll list other common uses of the positive lens.
(24) The simple magnifier is a single lens that lets us see objects that are too small to be seen clearly by the unaided eye. To see a small object distinctly with the unaided eye, we have to place the object as near to the eye as possible. However, as we said in the last paragraph, the normal eye can focus clearly only on objects no closer than approximately 10 inches. The simple magnifier shown in Figure 12 is an "optical instrument" that, when focused on a nearby tiny object, produces a magnified, virtual image at a convenient distance for clear vision.
Fig. 12
Virtual image formed by positive lens acting as a magnifier
(25) A searchlight is an optical device that collects light from an intense "point" source and transmits this light as a nearly parallel, well-collimated beam. In many cases this is accomplished with parabolic mirrors. But in principle it can be done with a large lens as shown in Figure 13.
Fig. 13
Simple example of a searchlight
(26) The small source in Figure 13 is shown exaggerated in size for clarity. It’s made up of points 1, 2, 3. Since the source lies in the focal plane of the lens, each point on the source leads to a beam of parallel light leaving the lens. For example, point 1 gives the parallel bundle ,
', ". Point 2 gives the parallel bundle ‚ , ‚ ', ‚ ". Point 3 gives the parallel bundle ƒ , ƒ ', ƒ ". You can see that, if the source becomes very small and point 2 and 3 move toward point 1, nearly all of the rays will be parallel to rays , ', ". The beam then is said to be well-collimated, progressing to the right with very little spreading or divergence.(27) Now consider the applications shown in Figure 14. Figure 14a shows the essential geometry of a motion-picture projector, where the object is located a distance more than one focal length (but less than two focal lengths) from the lens and is projected as a real, inverted, magnified image. If the object is moved to exactly two focal lengths from the lens, a real inverted image of the same size is formed two focal lengths on the other side of the lens. This scheme for one-to-one reproduction is used in a copy machine as shown in Figure 14b.
Fig. 14
Other applications of the positive lens
(28) Objects that lie some distance greater than twice the focal length from the lens are projected as real, inverted images of reduced size. This is often the case with optics in the ordinary camera, as shown in Figure 14c.
(29) Finally, if the object is very far away from the lens, the rays of light that enter the lens are essentially parallel to one another and image in the focal plane of the lens, as a tiny spot. This is the example shown in Figure 14d, where a simple positive lens is used to focus the collimated light from the distant sun or the highly parallel light from a laser. You should see that the geometry in Figure 14d is the "opposite" of the geometry for the searchlight in Figure 13. Here parallel light is focused as a spot. In Figure 13, light diverging from a tiny spot is transmitted on a parallel beam.
(30) Concave and convex meniscus lenses are used to correct myopia (nearsightedness) and hyperopia (farsightedness). The concave and convex meniscus lenses are used instead of regular concave or convex lenses to enable the eye to scan a large field of view and yet always be the same distance from the meniscus lenses. Figure 15 illustrates the operation of a normal eye, the problem with the nearsighted and farsighted eye, and the correction introduced with the appropriate meniscus lenses.
Fig. 15
Vision defects and corrections
Uses of Lens Systems
(31) Some uses for the single lens have been mentioned already. Complex optical tasks generally require the use of two or more lenses in an optical system. One such well-known lens system is the telescope, shown in Figures 16 and 17. The Galilean telescope, shown in Figure 16, gives an upright image of a distant object.
Fig. 16
Galilean telescope
(32) The Galilean telescope consists of a positive objective O and a negative lens eyepiece E. Their focal points FE and FO are in coincidence, as shown. If no eyepiece lens were present, rays from a distant object would, after refraction through the objective lens, meet to form a real, inverted image "i" in the focal plane. However, because these rays are intercepted at the eyepiece, in front of the focal plane, the rays are diverged and seem to the eye to be coming from an object of much larger dimensions. The dotted lines at angle b indicate the direction along which the tip of the virtual image is seen with the Galilean telescope the image is erect and magnified. The amount of magnification is the ratio of angle b to angle a. This type of telescope is preferred for use as field or opera glasses because it is very short and compact and gives a bright, erect image.
(33) The telescope in Figure 17 is called a celestial or astronomical telescope. is telescope uses two lens systems, the objective lens system and the eyepiece lens system. Rays from a distant object are shown entering a long-focal-length objective lens as a parallel beam. These rays are brought to a focus and form a real, reduced image in the focal plane of the objective, FO'.
(34) If we assume the distant object to be an arrow with the arrowhead upward, the image is real and inverted, as shown. The real image, viewed by the eye through the eyepiece lens system, is seen as a magnified, virtual image as shown by the dotted lines. The image, compared with the original object, is inverted. But this is not important when we look at stars, for example.
Fig. 17
Astronomical or celestial telescope
(35) The celestial telescope is the basis for many instruments used in optics. The transit, sight level, alignment telescope, and the collimator all use a telescope in one form or another.
(36) One use of a telescope of this type in laser work is for the function of beam expansion. As shown in Figure 18, if a beam of light from the laser is used to illuminate the eyepiece and therefore is sent through the telescope "backward," it will emerge from the objective lens larger in diameter than when it entered and the rays will be somewhat more collimated or parallel.
Fig. 18
Principle of beam collimation and expansion
(37) As shown in Figure 19, there are two different ways to produce beam expansion or beam reduction. The first method (Figure 19a) uses a convex lens followed by another convex lens. Note that the focal point F1 of lens L1 falls on the focal point F2 of lens L2. This beam expander/collimator often is called the Keplerian beam expander. It and the one shown in Figure l9b have names derived from alleged inventors of refracting telescopes that closely resemble the beam expanders.
Fig. 19
Two common types of beam expanders/collimators
(38) The second method uses a concave lens followed by a convex. Note again that the focal point F1 of lens L1 falls on the focal point F2 of lens L2. This is called a Galilean beam expander.
(39) In high-powered laser applications it’s important to use the second method of beam expansion. This is because the small beam spot created at the common focal points in the first method results in high energy densities, which may cause the air to break down or ionize.
(40) For either version of the two-lens beam expander, we can define the lateral magnification as
M = |
Equation 2 |
(41) Optics texts show that the lateral magnification of the beam expander is given simply by the ratio of the focal lengths,
M = |
Equation 3 |
(42) We also can show that, to a good approximation, the divergence angle of the expanded beam is related to the divergence angle of the incident unexpanded beam by,
q 2 = |
Equation 4 |
(43) Equations 2, 3, and 4 assume that the beam expander is focused properly. In other words, the distances between the center (approximately) of the lenses is equal to f2 – f1. Note that f2 can be either positive or negative.
(44) For laser applications it’s important to realize that, as the beam expander increases the beam diameter, it also decreases the beam divergence angle by the same amount. It’s usually necessary to first expand a beam before illuminating a distant target with a laser, if the beam size on the distant target is to be minimized.
(45) Another use of lens systems is in the compound microscope. The microscope is very similar to the telescope except that the objective lens now has a much smaller focal length. So it has a definite focal point close to the front lens. In the compound microscope shown in Figure 20, the objective lens forms an enlarged image I1 of the small object at O.
Fig. 20
Compound microscope
(46) The eye—viewing the image through the eyepiece—sees a much enlarged image according to the principles of the simple magnifier. Since the apparent size of the image is larger than the actual size of the object, the angle subtended at the eye is larger. So, there is magnification. It’s interesting to note that placing a short-focal-length lens in the front of a telescope changes it to a microscope. This is shown in Figure 21.
Fig. 21
Converting a telescope into a microscope
Problems in Lenses
(47) Even the best lenses have certain amounts of aberrations or deviations from perfectly formed images. It is well-known that in practice, lenses normally don’t perform exactly in accordance with a simple lens formula. This section will define some of these lens faults and discuss how to correct them.
(48) Aberration can be defined as a faulty image formation caused by failure of all the incident light rays from a point on the source to focus as the corresponding point image in the image plane. The types of defects or aberrations in the image that we will discuss are classified as:
|
occurs in first order for light that is not monochromatic | |
|
third-order "primary" or "Seidel" aberrations |
(49) Many beginning students of optics don’t realize that they really are learning an approximate theory of ray tracing. The elementary formulation often is called "first-order theory." It gets its name from the expansion of the sin q function,
sin q = q
– 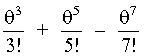 + …
+ …
(50) If the function sin q is approximated by q (measured in radians) then we are using a "first-order" theory. If we add the next term in the series, –q 3/3!, we’re said to be using a "third-order" theory. Note that second, fourth, etc. theories don’t exist because there are no odd power terms in the expansion.
(51) Although often it’s not shown clearly by instructors teaching beginning optics courses, most of the formulas you learn are only accurate to first order. Even the matrix theory that most laser students learn in optics is only accurate to first order. To this approximation, lenses and mirrors appear to image much better than they do in reality.
(52) If the third-order terms are included in the mathematics of our theory, we start to predict the imaging "problems" that we mention in this module. In fact we predict, through the mathematics, the existence of the last five "problems" listed above. These often are called the five "primary" or "Seidel" aberrations (spherical aberrations, coma, astigmatism, distortion, and field curvature). These are named in honor of Ludwig von Seidel (1821-1896) who first studied the mathematics of these effects in detail (in the 1850s).
(53) Although a mathematical description of these effects is not appropriate here, we will discuss briefly the five Seidel aberrations and the unrelated effect called "chromatic aberration." We also should note that modern lens-design software that runs on microcomputers is accurate to fifth order. It takes into account even higher-order aberrations than those studied by Seidel. Much of the task of modern optical engineers is minimizing these third-, fifth- and higher-order effects to produce exceptionally high-quality images, while keeping the size, weight and cost of the optical system within reason.
Chromatic Aberration
(54) A prism deviates blue light more than red light. Simple lenses do the same thing with the result that blue light comes to a focus nearer to the lens than red light. This defect is called chromatic aberration of the lens.
(55) Some photographic emulsions are most sensitive to light at the blue end of the spectrum. A lens with chromatic aberration may form an image that appears sharp to the eye, but it produces a blurred, out-of-focus image on the film negative. Figure 22 shows chromatic aberration. In the figure, white rays from a point object are split up inside the lens and come to separate foci that depend for their position on wavelength. Wavelengths range from about 4200 angstrom units at the blue end to 7500 angstrom units for the red end of the spectrum.
Fig. 22
Chromatic aberration
(56) The best correction for chromatic aberration is the use of a negative lens, made of a glass with a different index of refraction, in combination with a positive lens. The projection system shown in Figure 23 uses lenses, taken together, to correct for chromatic aberration.
Fig. 23
Achromatic projection lens system
(57) You saw in Figure 14a that a single biconvex lens can be used as a projection lens. In practice, however, a projection lens consists of a pair of lenses that are corrected for chromatic aberration. Since the projected image is generally large compared to the object, aberrations (defects in perfect focus) will be quite noticeable. Figure 23 shows that a magnified image will be formed on a distant screen if a well-illuminated object or real image is placed in the focal plane of a projection lens.
Spherical Aberration
(58) Rays that come from an object on the axis of a lens and pass through a portion of the lens near the center come to a focus at a certain point on the axis of the lens. Rays from this same object point that pass through the lens near the edges of the lens should come to a focus at the same point, if a good image is to be formed. In practice, because of spherical aberration, the marginal rays tend to come to a different point than do the "center" rays. The difference between these focal points is caused by spherical aberration of the lens. Longitudinal spherical aberration occurs when the marginal and paraxial rays passing through a positive lens fail to meet at a common focal point.
Fig. 24
Spherical aberration
(59) Spherical aberration is shown in Figure 24 for a bundle of parallel rays, all originating from an on-axis point of a distant object. Spherical aberration can be corrected with a diaphragm in front of or behind the lens that cuts out the marginal ray. Another possible correction occurs with a specially ground meniscus lens.
Coma
(60) This type of aberration is restricted to "off-axis" image points. In some respects we can consider it as spherical aberration of an oblique bundle of rays. Since the lens has no symmetry about a line passing through the center of the lens and an off-axis point in the image, the effects of coma are complex and unsymmetrical. Coma is shown by Figure 25. (No hard rule for elimination of coma can be laid down.) It might help to cover part of the lens with a diaphragm. If this fails the only choice is to discard the faulty lens.
Fig. 25
Coma
Astigmatism
(61) Astigmatism is the inability of a lens to bring all the rays from a vertical plane to the same point as the rays from a horizontal plane. This problem is shown is Figure 26. Astigmatism can be improved with special lens shapes and by reducing the lens aperture, thus eliminating the offending marginal rays.
Fig. 26
Astigmatism
Distortion
(62) Distortion is the magnification of image points near the optical axis more (or less) than the magnification of image points at off-axis positions. Distortion causes parallel lines to bow and images to lose their proportion. When axial magnification is greater than off-axis magnification, the lens has positive or barrel distortion. When axial magnification is less, it has negative or pincushion distortion. The effects of these types of distortion are shown in Figure 27 for a uniform and parallel grid image.
Fig. 27
Effects of distortion on squared patterns
(63) Distortion does not depend on lens aperture. It can be corrected only with specially ground lenses or filter optics.
Curvature of Field
(64) Curvature of field often is called "Petzval field curvature" in honor of the Hungarian mathematician Josef Max Petzval (1807-1891) who first described it in mathematical detail. It is shown in Figure 28. Note that, unlike the assumptions made in an elementary first-order theory, objects lying in a plane don’t generally image into a plane. The image "surface" is in general curved either concave or convex when viewed from the direction of the object.
(65) To a good approximation, for spherical lenses, the image "surface" is paraboloidal in shape. This condition is unacceptable, for example, in the case of a 35-mm slide projector, where the object is a plane (the slide) and the image usually also is focused on a plane (the screen). If just a simple, spherical lens were used to project the image, the center and the edge of the screen could not be focused simultaneously.
Fig. 28
Field curvature. Object in flat image plane focuses into curved image surface.
Not drawn to scale.
(66) To minimize this problem, combinations of positive and negative lenses usually are used. A typical high-quality 16-mm movie projector lens is shown in Figure 29. The negative elements of the lens combine with the positive focusing lenses to form a so-called "field flattener," that greatly minimizes the curvature of field.
Fig. 29
High-quality projector compound lens containing field-fattening elements. (Hecht)
Reducing Aberrations
(67) A complete description of ways to minimize lens aberrations is beyond the scope of this module. We can make a few closing statements about methods that can be used if aberrations become a particular problem in an optical system. Some of these aberration-reducing methods are relatively easy. Others require an intimate knowledge of the details of lens system design. In general, reduction of the Seidel aberrations (and chromatic aberration) requires one or more of the following four basic techniques:
• Careful choice of the curvature of the surfaces and the sequence in which the particular surfaces appear in the optical system.
• Using combinations of lenses.
• Reducing the system aperture with one or more stops.
• Producing lenses with aspheric surfaces.
(68) Dramatic reduction in some aberrations can be achieved by simply turning the lens around (method #1). Reducing the aperture or "stopping down" a system usually will cause a significant reduction in aberrations (except curvature of field), but with a concurrent loss in image intensity.
Optical Coatings
(69) An uncoated lens with an index of refraction of 1.50 will reflect about 4% of incident light, normal to each surface. In some applications, particularly where a large number of optical elements lie in the optical path, such loss may be unacceptable. To reduce reflective losses, optical elements generally are coated with one or more layers of transparent material. Figure 30 shows the effect of coating an optical substrate with an antireflection (AR) coating.
Fig. 30
Ray trace of a single layer AR coating. The thickness t of the coating is chosen
such that the rays reflecting from interfaces (1) and (2) are 180° out of phase.
(70) If the thickness and index of refraction of the coating are chosen properly, the rays that reflect from interfaces (1) and (2) will be 180° out of phase and cancel.
(71) A simple analysis shows that, for light striking the surfaces at normal incidence, the minimum thickness t of the coating should be given by
t = |
Equation 5 |
| where: | l =
Wavelength of light in a vacuum n1 = Index of refraction of the coating material |
(72) Maximum cancellation occurs if the two reflected waves are of the same amplitude. If we assume that little absorption occurs in the coating, the reflected rays will be equal in amplitude if,
n1
= |
Equation 6 |
(73) For a typical case of a flint (n2 = 1.72) glass lens surrounded by air, the ideal coating index should be
n1
= |
Equation 7 |
(74) MgF2 with an index of refraction of 1.38 is a close match to the ideal value for many types of common glass. Single-layer coatings usually are "tuned" for the middle of the visible spectrum, in applications such as camera and projector lenses. They don’t work quite as efficiently at the red and blue ends of the visible spectrum. So the reflection from these coated optics often appears purple to the eye.
(75) A single layer of MgF2 can greatly reduce reflections from a surface, as shown in Figure 31. Note that the effectiveness of the AR coating depends dramatically on the index of refraction of the substrate material.
Fig. 31
Reflectance of coated surface of index ng when coated with a
quarter wavelength of magnesium fluoride (index = 1.38). (Meiles Griot)
(76) Figure 32 shows the effect of wavelength on the reflectance from an optical surface with a single AR coating layer. Although this coating is optimized for 550 nm, it’s surprisingly insensitive to incident wavelength. The effectiveness of MgF2 as an antireflection coating is increased dramatically with increasing refractive index of the component material (see Figure 31). This means that, for use on high-index materials, there is often little point in using more complex coatings.
Fig. 32
Reflectance curve for MgF2 on BK 7 optical glass. (Melles Griot)
(77) For a further reduction in reflectance, multilayer AR coatings can be used. Multilayer coatings tend to be considerably more expensive and more susceptible to mechanical and optical damage.
(78) Particularly when used with high-energy pulsed lasers, you must consider the damage threshold of optical coatings. The probability of damage occurring to the AR coating depends on a number of factors including: the coating and substrate material, defects or contaminants in the coating or substrate, polarization of the incident light, wavelength of the light, and peak value of the electric field caused by the incident light. Lens manufacturers usually will specify the nominal damage threshold for coated and uncoated optics that they supply. Modern AR coatings can be very resistant to laser-induced damage. For example, a hard single-layer oxide coating typically will withstand 5 joules/cm2 in 1-nsec pulses from an Nd:YAG laser irradiating the surface at an incident angle of 45°. This represents an irradiance of 5 GW/cm2.

1. Explain the following terms, concepts, or instruments. Your explanations should convey the same meanings given in the text.
a. Converging lens
b. Diverging lens
c. Power of a lens
d. Focal length of a lens
e. Lens systems
f. Collimation
g. Spherical aberration
h. Chromatic aberration
i. Coma
j. Astigmatism
k. Distortion
2. From the given cross-sectional diagrams identify the following lenses:
a. ________________ b. ________________
c. ________________ d. ________________
e. ________________ f. ________________
g. ________________ h. ________________
3. Explain, in your own words, the procedure for experimentally determining the focal length of a concave and a convex lens.
4. When working with high-power lasers, why is it necessary to use a beam expander made of a negative and a positive lens rather than one made from two positive lenses? Use accurately drawn ray diagrams to help explain your answer.
5. Using an accurately drawn diagram illustrate the difference between spherical aberration and chromatic aberration.
6. Depth of field is the range of distances over which a camera is in satisfactory focus. Use the concept of spherical aberration to explain why a camera has better depth of field when the lens aperture is small than it has when the lens aperture is large.
7. A 1.00-watt argon laser with an exit-beam diameter of 2.00 mm and a full-angle beam divergence of 1.20 mrad is shined onto a target 3.00 km away. Neglecting atmospheric loss, what is the average irradiance on the target? The output beam of the laser is directed into a Galilean beam expander comprised of a negative lens (f = –7.00 mm) and a positive lens (f = +25.0 cm). Assume that the overall transmission of the bearn expander/collimator is 92% and that it is focused properly. Calculate the average irradiance on the distant target.
8. The reflectance from a transparent surface is given by
where T is the fractional amount of light reflected from the interface and n is the index of refraction of the transparent medium. (The other side of the interface is assumed to have an index = 1.00.) For a borosilicate crown glass lens, illuminated at normal incidence with a red HeNe laser beam, what is the reflective loss (in percent) per surface?
9. What is the thinnest coating of MgF2 that can be applied to a borosilicate crown glass lens designed to work at normal incidence with a red HeNe laser beam? After the coating is applied, what is the approximate reflective loss in percent per surface? (See Fig. 31.)
10. Contact three vendors regarding the purchase of the following lens:
Type: Plano-convex
Material: Any high-quality optical glass transparent in the visible.
Focal length +20 cm.
Diameter: At least 2 cm.
Coating: Single or multilayer, "tuned" for use with the ruby laser line.
Obtain as much information as you can regarding the lenses, surface and bulk material properties, aberrations, AR coating efficiency, coating damage threshold, etc., and of course, cost.
If you were planning to use this lens to focus a 5 joule ruby laser (pulse width = 250 m sec), expanded beam diameter = 2.0 cm, onto a workpiece, which lens would you select? Are there other aspects of your application that you need to know to decide?

Optical bench or table with optical mounts
2 Positive lenses (one short focal length < 5 cm, one long focal length 720 cm)
2 Negative lenses (one short focal length < 5 cm, one long focal length 720 cm)
Ground glass screen
HeNe laser
2 Optical stops (1 center stop, 1 edge stop)
Cross-line object
Illuminating lamp
Metric ruler or metric caliper

Determining the Focal Length of a Lens
(79) You can determine the focal length of an unknown lens in several different ways. The simplest of these is described here. This experimental determination of focal length depends on the operational definition of focal length. The focal length of a lens is the distance from the center of the lens to the point where parallel collimated rays of light from a distant source are focused by the lens. This length normally is given in meters.
(80) Set up the optical bench as shown in Figure 33. Place a convex (positive) lens of unknown focal length in the lens holder on the optical bench. Point the optical bench at some distant bright object, for instance, a lamp in a long corridor. The distance should be not less than 50 meters. Also place a ground glass screen in its holder on the optical bench and form an image of the distant object produced by the lens on this screen. The difference between the readings of the lens holder and the ground glass screen holder will be the focal length of the lens. You might have to make a number of independent readings and average them for accuracy.
Fig. 33
Arrangement to determine focal length
(81) Determination of focal length of a concave (negative) lens takes a little more effort. You first must set up the meter bench as before and slide the ground glass screen until the bright object is in focus in front of a convex lens. Write down this position of the screen (S1). Then place the concave lens of unknown focal length between the convex lens and this position. This is shown in Figure 34.
Fig. 34
Determining focal length of a concave lens
(82) When you have noted S1 and inserted the concave lens, move the screen until the image is again in focus. This is shown as screen position S2. Now use the lens system formula to calculate the focal length of the concave lens. This formula (rewritten for this purpose) is
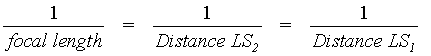
As before, take a number of independent readings for accuracy.
The Celestial Telescope Used as a Beam Expander
(83) Mount on an optical bench the components necessary to produce a Keplerian beam expander/collimator. An arrangement similar to that shown in Figure 19a of this module is sufficient.
(84) Shine a laser beam "backward" through the "telescope." Make any adjustments necessary to produce an expanded, collimated output beam. Record the focal lengths of the lenses and the diameters of the input and output beams. Repeat for the Galilean beam expander/collimator shown in Figure l9b.
Demonstration of Spherical Aberration and One Correction
(85) The effect of spherical aberration is that light through the outer edge of the lens comes to a focus at a point on the axis nearer the lens than light through the center. This causes the image to appear blurred over the entire field.
(86) Place the lamp, the cross-line object, the convex lens, and the ground glass screen on the optical bench or table as shown in Figure 35.
Fig. 35
Arrangement to demonstrate spherical aberration
(87) Place the "center-of-lens" stop—shown in Figure 36¾ in front of the lens and move the screen until the image of the cross line is sharply in focus.
Fig. 36
Center-of-lens stop
(88) Next, move the center-of-lens stop and insert the "edge-of-lens" stop shown in Figure 37.
(89) Move the ground glass screen back until the image is once again in focus. The amount of spherical aberration the lens has is indicated by the distance between these two focal points. Spherical aberration normally is corrected by using an edge-of-lens stop or a diaphragm so that only the center portion of the lens is used.
Fig. 37
Edge-of-lens stop
(90) Repeat the above procedure with a larger-diameter lens. Compare the spherical aberration of the two lenses.

Hecht, E. Optics. 2nd edition. Addison Wesley, 1987.
Jacobs, Donald H. Fundamentals of Optical Engineering. McGraw-Hill Book Co., 1943.
Jenkins, Francis A., and Harvey E. White. Fundamentals of Optics. 4th edition. McGraw-Hill Book Company, 1976.
Kingslake, Rudolf. Applied Optics and Optical Engineering. Volume III. Academic Press, Inc., 1965.
The Newport Corporation Catalog No. 100. Newport Corporation, 18235
Mt. Baldy Circle, Fountain Valley, CA 92728-8020, (714) 963-9811.
Optics Guide 3. Melles Griot, 1770 Kettering Street, Irvine, CA 92714, (714) 261-5600.
Oriel Corporation Catalog Vol III. Oriel Corporation, 250 Long Beach Blvd., Stratford, CT 06497-0872, (203) 377-8282.
Pedrotti, Frank L., and Leno S. Pedrotti. Introduction to Optics. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1987.
Pollock, H. W. Applied Physics. 2nd edition. Prentice-Hall, 1971.