IEEE TRANSACTIONS ON ULTRASONICS, FERROELECTRICS, AND FREQUENCY CONTROL, VOL. 35, NO. 3, MAY 1988
© 1996 IEEE. Personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution to servers or lists, or to reuse any copyrighted component of this work in other works must be obtained from the
IEEE.
The Acceleration Sensitivity of Quartz Crystal Oscillators: A Review
Invited Paper
RAYMOND L. FILLER, MEMBER, IEEE
Manuscript received March 24, 1987; revised May 4, 1987. (Corrected by the author, 1999)
The author is with the U.S. Army Electronics Technology and Devices Laboratory
(LABCOM), Attn: SLCET-EQ, Fort Monmouth, NJ 07703-5000.
IEEE Log Number 8719296.
Abstract–The acceleration sensitivity of quartz crystal oscillators is assuming increasing significance in modern communications, navigation, radar, and identification systems. This paper is a tutorial and a review of the various aspects of acceleration sensitivity. The topics to be discussed are the consequences of acceleration sensitivity in crystal oscillators on the Allan deviation, including the effects of sinusoidal and random vibration, phase noise and integrated phase jitter; the vector nature of quartz resonator sensitivity; the theoretical description of the cause of the acceleration sensitivity of quartz resonators; techniques for he measurement of acceleration sensitivity; and the effect of frequency multiplication on acceleration effect. In addition, various techniques currently being used or developed for reducing the effective acceleration sensitivity will be discussed. The techniques fall into three general categories: reduction of the acceleration sensitivity of the resonator passive techniques that use compensating elements in the oscillator feedback loop, e.g., a second resonator or an acceleration sensitivity capacitor; and active acceleration compensation schemes that sense the acceleration and feedback a compensating signal to a tuning network.
INTRODUCTION
THERE has been an awareness of acceleration effects in frequency sources at least since the advent of missile and satellite applications [1]-[6], Doppler radars [7], [8], and other systems requiring extremely low noise [9], [10]. There has not, however, been a general appreciation of the magnitude of the problem. As a case in point, there is little or no mention of acceleration sensitivity in the general texts on quartz crystal oscillators and resonators or of vibration induced phase noise in radar textbooks.
Time-dependent acceleration, i.e., vibration, can cause a large increase in the noise level of a quartz crystal oscillator. In fact, in frequency sources operating on mobile platforms, the vibration-induced phase noise is usually greater than all other noise sources combined.
High-stability frequency sources, including atomic standards, contain quartz crystal resonators. One result of the evolution of electronics, i.e., the transition from tubes to transistors, and from point-to-point wiring to printed circuits, is the establishment of the quartz crystal resonator as the most acceleration-sensitive component in frequency sources. This paper will review the causes and effects of acceleration sensitivity of bulkwave quartz crystal resonators, and the methods that reduce or compensate for that sensitivity. Most of what is discussed is equally relevant to surface-acoustic-wave (SAW) and shallow-bulk-acoustic-wave (SBAW) devices.
THE EFFECT OF ACCELERATION ON A CRYSTAL RESONATOR
A quartz crystal resonator subject to a steady acceleration has a slightly different series resonant frequency than the same resonator experiencing zero acceleration [1]. Furthermore, it has been observed that the magnitude of the frequency shift is proportional to the magnitude of the acceleration, and is also dependent upon the direction of the acceleration relative to a coordinate system fixed to the resonator [11]. It has been shown, empirically, that the acceleration sensitivity of a quartz crystal resonator is a vector quantity [12]. Therefore, the frequency during acceleration can be written as a function of the scalar product of two vectors
![]()
where ![]() is the resonant
frequency of the resonator experiencing acceleration a,
is the resonant
frequency of the resonator experiencing acceleration a, ![]() is the frequency with no acceleration
(referred to as the carrier frequency), and
is the frequency with no acceleration
(referred to as the carrier frequency), and ![]() is the acceleration-sensitivity vector. It can be seen
from (1) that the frequency of an accelerating resonator is a maximum when tile
acceleration is parallel to the acceleration-sensitivity vector; it is a minimum when the
acceleration is antiparallel to the acceleration-sensitivity vector. An important result
of (1) is that the frequency shift,
is the acceleration-sensitivity vector. It can be seen
from (1) that the frequency of an accelerating resonator is a maximum when tile
acceleration is parallel to the acceleration-sensitivity vector; it is a minimum when the
acceleration is antiparallel to the acceleration-sensitivity vector. An important result
of (1) is that the frequency shift, ![]() is zero for any acceleration in the plane normal to the
acceleration-sensitivity vector.
is zero for any acceleration in the plane normal to the
acceleration-sensitivity vector.
The frequency shift described in (1) is also induced by the acceleration due to gravity (even without motion). This is commonly referred to as "2 g-tipover." During "2-g-tipover," the magnitude of the acceleration is 1 g in the direction towards the center of the earth. (The magnitude of acceleration given in this paper will be in units of g, i.e., the magnitude of the earth's gravitational acceleration at sea level, 980 cm/s2.) When a resonator is rotated 180o about a horizontal axis, the scalar product of the acceleration and the unit vector normal to the initial "top" of the resonator goes from -from -1 g to +1 g, which is a difference of 2 g. Fig. 1 shows actual data of the fractional frequency shift of a resonator (operating in an oscillator) when the oscillator is rotated about three mutually perpendicular axes in the earth's gravitational field. For each curve, the axis of rotation is held horizontal. The sinusoidal shape of each curve is a consequence of the scalar product being proportional to the cosine of the angle between the acceleration-sensitivity vector and the acceleration due to gravity.
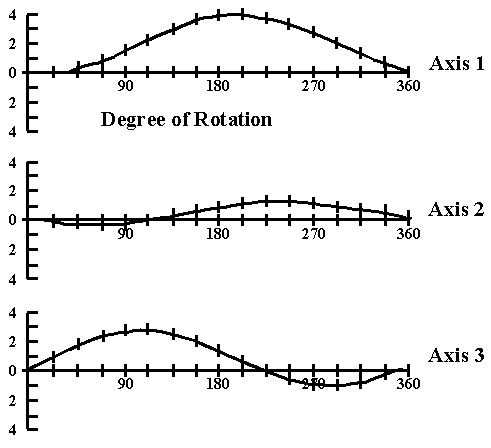
Fig. 1. "2-g tipover," frequency changes versus rotation in earth's gravitational field for three mutually perpendicular axes.
THE EFFECT OF VIBRATION ON A CRYSTAL RESONATOR
In most applications, the magnitude of the acceleration is time-dependent. The magnitude of the acceleration-sensitivity vector, for acceleration amplitudes commonly encountered, is independent of acceleration amplitude [11]. The time-dependent frequency shift due to a complex vibration can, therefore, be determined from the sum of the individual sinusoidal components, i.e., the system is linear and superposition holds. Simple sinusoidal vibration will be discussed first; the extension will then be made to random vibration.
Simple harmonic motion will be assumed, with an acceleration given by
![]()
where ![]() is the peak acceleration vector in units of g,
is the peak acceleration vector in units of g, ![]() , is the frequency of
vibration in Hertz, and t is time in seconds. The variation of the frequency with time can
be determined by combining (2) with (1), resulting in
, is the frequency of
vibration in Hertz, and t is time in seconds. The variation of the frequency with time can
be determined by combining (2) with (1), resulting in
![]()
The behavior of the device can be described by defining a rectangular
coordinate system fixed to the resonator. The acceleration-sensitivity vector and the
acceleration vector can then be described in terms of the three unit vectors defined by
that coordinate system. Therefore (3) can be transformed into a scalar equation containing
the three (i, j, and k) components of ![]() and
and ![]() , i.e.
, i.e.
![]()
This can be rewritten as
![]()
where
![]()
is the peak frequency shift due to the acceleration ![]() .
.
There are three quantities with units of frequency to keep in mind: ![]() It can be
seen from (5) that the output frequency deviates from the center frequency,
It can be
seen from (5) that the output frequency deviates from the center frequency, ![]() by the amount
by the amount ![]() at a rate of
at a rate of ![]() This is shown
schematically in Fig. 2. Each plot is the instantaneous output
frequency of a crystal oscillator while undergoing a vibration at frequency
This is shown
schematically in Fig. 2. Each plot is the instantaneous output
frequency of a crystal oscillator while undergoing a vibration at frequency ![]() Fig. 3(b) is the voltage versus time at the output of the same crystal
oscillator showing, in a much exaggerated way, the variation in the frequency with
acceleration amplitude. Fig. 3(a) is the acceleration waveform.
Fig. 3(b) is the voltage versus time at the output of the same crystal
oscillator showing, in a much exaggerated way, the variation in the frequency with
acceleration amplitude. Fig. 3(a) is the acceleration waveform.
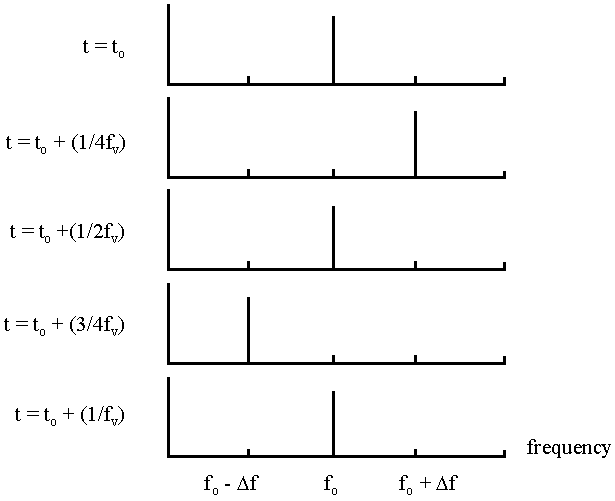
Fig. 2. Instantaneous "carrier" frequency for several instants during one cycle of vibration.
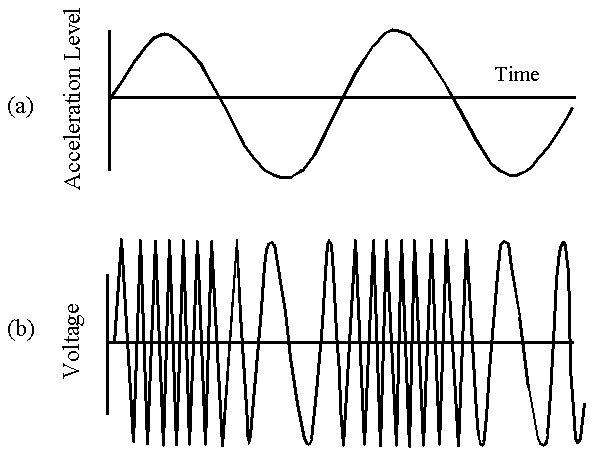
Fig. 3. (a) Acceleration level versus time. (b) Resulting oscillation output showing frequency modulation.
FREQUENCY DOMAIN
It is very useful to transform the effect of vibration into the frequency domain. This will allow the formulation of a convenient measurement scheme and allow comparison of vibration effects to more familiar forms of phase noise.
The voltage appearing at the output of an oscillator is given by
![]()
where the phase ![]() is derived from the frequency by
is derived from the frequency by
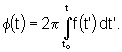
When the oscillator frequency is varying due to simple harmonic acceleration modulating the resonant frequency of the resonator, the phase in (7) becomes, using (5) and (8),
![]()
When (9) is inserted into (7), the result is
![]()
Equation (10) is the expression for a frequency-modulated signal. It can be expanded in an infinite series of Bessel functions [13] resulting in [14]
![]()
![]()
![]()
![]()
![]()
where ![]() is the modulation index (from standard FM theory).
is the modulation index (from standard FM theory).
The first term in (11) is a sine wave at the carrier
frequency with an amplitude, relative to ![]() of
of ![]() The other terms are vibration-induced sidebands at
frequencies
The other terms are vibration-induced sidebands at
frequencies ![]() etc. In analogy with common phase-noise notation [16],
the ratio of the power in the nth vibration-induced sideband to the power in the
carrier, denoted by
etc. In analogy with common phase-noise notation [16],
the ratio of the power in the nth vibration-induced sideband to the power in the
carrier, denoted by ![]() is given by
is given by
![]()
or, more commonly expressed in decibels as
![]()
where dBc refers to dB relative to the carrier and the subscript v refers to the vibration.
SMALL MODULATION INDEX
Several approximations can be made if the modulation index is less than 0.1. This is the case for most frequency standards in the HE band experiencing "normal" accelerations of 10 g or less at acceleration frequencies above a few hertz. The approximations are
![]()
![]()
![]()
Therefore, after combining (132) and (14):
![]()
For small modulation index, therefore, most of the power is in the carrier
and a small amount is in the first sideband pair (upper and lower). The amplitudes of the
higher sidebands are negligible. The condition of small modulation index permits ![]() to be equated
to
to be equated
to ![]() [16].
[16].
As an example, consider a 5-MHz oscillator with a
vibration sensitivity of 2 x 10-9/g. If the oscillator experiences an acceleration of 5 g
along the direction of the acceleration-sensitivity vector, the value of ![]() is (5 x 106
Hz) * (5 g) * (2 x 10-9/g) = 0.05 Hz. The modulation index and
is (5 x 106
Hz) * (5 g) * (2 x 10-9/g) = 0.05 Hz. The modulation index and ![]() for several vibration
frequencies are shown in Table I. It can be seen that
for several vibration
frequencies are shown in Table I. It can be seen that ![]() falls off at
6 dB per octave (20 dB per decade). A consequence of linearity at low vibration levels is
that these sinusoidal accelerations are independent. The amplitude at any frequency is the
same if the bright lines are excited separately or in combination. The first three of
these vibration induced sidebands and the carrier are shown in a typical spectrum analyzer
output in Fig. 4.
falls off at
6 dB per octave (20 dB per decade). A consequence of linearity at low vibration levels is
that these sinusoidal accelerations are independent. The amplitude at any frequency is the
same if the bright lines are excited separately or in combination. The first three of
these vibration induced sidebands and the carrier are shown in a typical spectrum analyzer
output in Fig. 4.
TABLE I
First Sideband Level For A 5-MHz Oscillator
With An Acceleration Sensitivity Of 2 x 10-9/g
Experiencing An Acceleration Of 5 g Peak
Fv (Hz) |
b |
L (dBc) |
5 |
0.01 |
-46 |
25 |
0.002 |
-60 |
50 |
0.001 |
-66 |
500 |
0.0001 |
-86 |
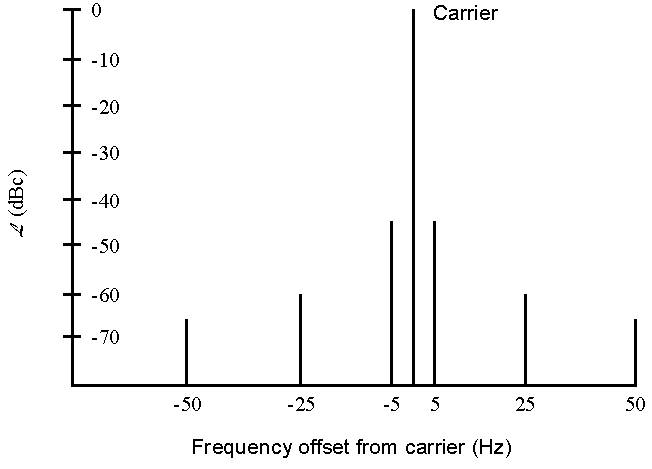
Fig. 4. Vibration-induced sidebands and carrier resulting from sinusoidal acceleration at 5 Hz, 25 Hz, and 50 Hz.
FREQUENCY MULTIPLICATION
Phase noise during vibration is of great concern in
systems such as radar, navigation, and satellite communications, where the frequency of
the crystal oscillator is multiplied up to the microwave region. Upon frequency
multiplication by a factor of N. the vibration frequency ![]() is unaffected since it is an external
influence. The peak frequency change due to vibration,
is unaffected since it is an external
influence. The peak frequency change due to vibration, ![]() , however, becomes
, however, becomes
![]()
The modulation index ![]() is therefore increased by a factor of N. Expressed in
decibels, frequency multiplication by a factor N increases the phase noise by 20 log N.
is therefore increased by a factor of N. Expressed in
decibels, frequency multiplication by a factor N increases the phase noise by 20 log N.
The relationship between the vibration-induced phase noise of two oscillators with the same vibration sensitivity and different carrier frequencies is
![]()
Where ![]() is the sideband level, in dBc, of the oscillator at frequency
is the sideband level, in dBc, of the oscillator at frequency ![]() and
and ![]() is the
sideband level of the oscillator at frequency
is the
sideband level of the oscillator at frequency ![]() This is identical to the "20 log
N" term associated with the increase in phase noise due to frequency multiplication.
Again, this relationship holds only if
This is identical to the "20 log
N" term associated with the increase in phase noise due to frequency multiplication.
Again, this relationship holds only if ![]()
LARGE MODULATION INDEX
If the modulation index ![]() is larger than about 0.1, the
approximations made in (14) are not valid. This often occurs in UHF and higher frequency
systems [9]. Frequency multiplication to a higher frequency is
indistinguishable from direct frequency generation at the higher frequency. For example,
when a 2 x 10-9/g sensitivity 5 MHz oscillator's frequency is multiplied by a factor of
308 to generate a frequency of 1575 MHz, its output will have identical vibration-induced
sidebands to a 1575 MHz SAW oscillator with a
is larger than about 0.1, the
approximations made in (14) are not valid. This often occurs in UHF and higher frequency
systems [9]. Frequency multiplication to a higher frequency is
indistinguishable from direct frequency generation at the higher frequency. For example,
when a 2 x 10-9/g sensitivity 5 MHz oscillator's frequency is multiplied by a factor of
308 to generate a frequency of 1575 MHz, its output will have identical vibration-induced
sidebands to a 1575 MHz SAW oscillator with a
sensitivity of 2 x 10-9/g. At 5 g acceleration, for example, the
vibration-induced sidebands produced by the 1575 MHz oscillator and the 5 MHz oscillator
multiplied by 308 are shown in Table II. It can be seen that the
values of ![]() in Table II are much greater than those in Table
I for the same vibration frequency. This is a consequence of the ratio of output
frequency to vibration frequency being much larger. It is possible, as can be seen in this
example, for the sidebands to be larger than the carrier. Also, there are even conditions
where the carrier disappears and the value of
in Table II are much greater than those in Table
I for the same vibration frequency. This is a consequence of the ratio of output
frequency to vibration frequency being much larger. It is possible, as can be seen in this
example, for the sidebands to be larger than the carrier. Also, there are even conditions
where the carrier disappears and the value of ![]() goes to infinity, e.g., when,
goes to infinity, e.g., when, ![]() equals 2.4,
that is, all of the power is in the sidebands and none is in the carrier.
equals 2.4,
that is, all of the power is in the sidebands and none is in the carrier.
ALLAN DEVIATION
The effect of sinusoidal phase modulation on the Allan deviation of a frequency standard has been shown [15] to be given by
![]()
where ![]() is the peak phase deviation,
is the peak phase deviation, ![]() is the frequency of the phase modulation, and t is the
measurement time. It can be seen from (9) that the magnitude of the maximum phase
deviation for a single vibration-induced sideband is
is the frequency of the phase modulation, and t is the
measurement time. It can be seen from (9) that the magnitude of the maximum phase
deviation for a single vibration-induced sideband is ![]() Therefore, the vibration-induced Allan
deviation of a frequency standard with an acceleration sensitivity of
Therefore, the vibration-induced Allan
deviation of a frequency standard with an acceleration sensitivity of ![]() subjected to
acceleration
subjected to
acceleration ![]() at a frequency of
at a frequency of ![]() is
is
![]()
This effect is shown in Fig. 5. The frequency standard is assumed to have an Allan deviation of (1 x 10-12/t)2 when not being accelerated.
A plausibility argument for the occurrence of the peaks
and valleys in Fig. 5 is that the average frequency, as given in (5),
is ![]() for
an averaging time equal to an integer multiple of the period of the vibration. Since this
is a constant, the variance is zero. The average frequency departure from
for
an averaging time equal to an integer multiple of the period of the vibration. Since this
is a constant, the variance is zero. The average frequency departure from ![]() is a maximum
when the averaging time is an integer multiple of one-half the period of the vibration.
Therefore, the peaks in Fig. 5 occur when
is a maximum
when the averaging time is an integer multiple of one-half the period of the vibration.
Therefore, the peaks in Fig. 5 occur when ![]() and the valleys occur when
and the valleys occur when ![]() where n = 0,
1, 2, 3,.
where n = 0,
1, 2, 3,.
TABLE II
First Sideband Level For A 1575-MHz Oscillator
With An Acceleration Sensitivity Of 2 x 10-9/g
Experiencing An Acceleration Of 5 g Peak
Fv (Hz) |
b |
L (dBc) |
5 |
3.15 |
+2.3 |
25 |
0.63 |
-9.6 |
50 |
0.315 |
-16.0 |
500 |
0.0315 |
-36.0 |
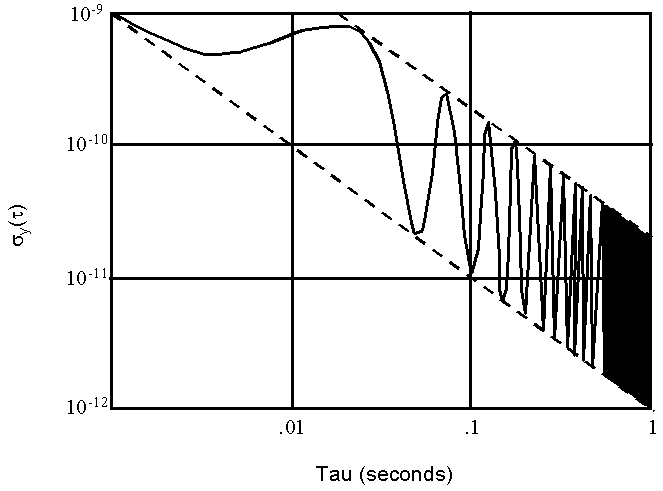
Fig. 5. Sigma of y of oscillator with acceleration-sensitivity of 1 ppb/g during 1-g vibration at 20 Hz.
RANDOM VIBRATIONS
In most situations the acceleration experienced by a frequency standard is
not simple harmonic motion; it is random, i.e., the vibratory power is randomly
distributed over a range of frequencies, phases, and amplitudes. The acceleration can be
described by its power spectral density G( f ). The power spectral density of frequency
fluctuations Sv(f) can be obtained by multiplying the power spectral density of
acceleration by the square of the acceleration sensitivity in (Hz/g)2. ![]() is related
to Sv, if the modulation index is small, by [16]
is related
to Sv, if the modulation index is small, by [16]
![]()
Therefore, ![]() for random vibration is given by
for random vibration is given by
![]()
As an example, consider the random acceleration spectrum given in the upper right of Fig. 6. G(f), in units of g2/Hz, is given by
![]()
![]()
![]()
![]()
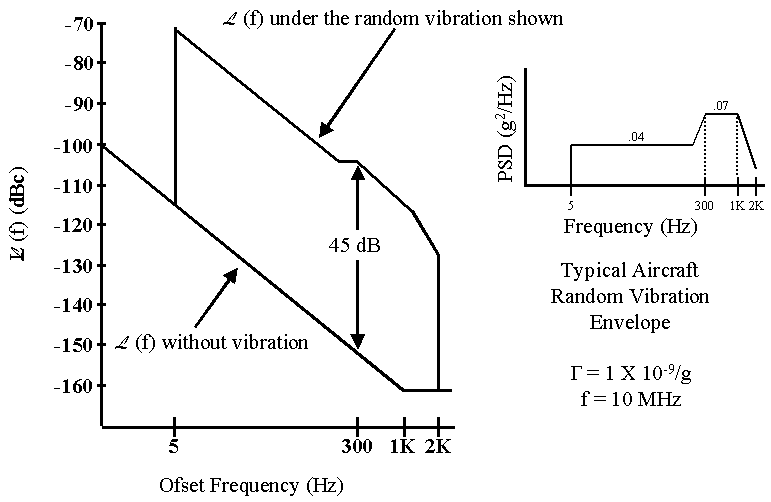
Fig. 6. Ramdom vibration-induced phase noise and random vibration envelope.
If the vibration sensitivity is 1 x 10-9/g and the oscillator is operating at
10 MHz, the peak frequency deviation is 0.01 Hz. Therefore, ![]() is
is
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
which is shown in Fig. 6. Note that outside of the vibration frequency range defined by the given acceleration spectrum, the phase noise is identical to that of a nonaccelerated device.
INTEGRATED PHASE NOISE AND PEAK PHASE EXCURSION
Specialists in crystal resonators and oscillators generally characterize
phase noise by ![]() Many users of crystal oscillators, however, characterize phase noise in
terms of "phase jitter." Phase jitter is the phase noise integrated over the
system bandwidth. Similarly, in phase-lock loops, it is the magnitude of the phase
excursions that determines whether or not the loop will break lock under vibration.
Many users of crystal oscillators, however, characterize phase noise in
terms of "phase jitter." Phase jitter is the phase noise integrated over the
system bandwidth. Similarly, in phase-lock loops, it is the magnitude of the phase
excursions that determines whether or not the loop will break lock under vibration.
One can use the previous example to investigate the effect of vibration on
integrated phase noise. Integrated phase noise is defined, for the band ![]() as
as
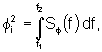
where ![]() is the spectral density of phase, equal to 2
is the spectral density of phase, equal to 2![]() In the frequency band of 1 Hz
to 2 KHz, the phase noise of the nonvibrating oscillator from Fig. 6
is given by
In the frequency band of 1 Hz
to 2 KHz, the phase noise of the nonvibrating oscillator from Fig. 6
is given by
![]()
![]()
and the integrated phase noise in the same band is
![]()
Therefore
![]()
While the oscillator is vibrating, the phase noise is given by (25) in the band from 1 Hz to 5 Hz, and by (23) in the band from 5 Hz to 2000 Hz. The integrated phase noise is
![]()
![]()
![]()
![]()
![]()
![]()
Therefore
![]()
While the oscillator is vibrating, it can be seen that the integrated phase
noise is 4000 times that of the noise when it is not vibrating and the rms phase
deviation, ![]() is about 60 times larger during vibration.
is about 60 times larger during vibration.
When the oscillator is subjected to a simple sinusoidal vibration, the peak phase excursion follows from (9), i.e.,
![]()
For example, if our 10 MHz, 1 x 10-9/g oscillator is subjected to a 10 Hz sinusoidal vibration of amplitude 1 g, the peak vibration-induced phase excursion is 1 x 10-3 radians. If this oscillator is used as the reference oscillator in a 10 GHz radar system, the peak phase excursion at 10 GHz will be 1 red. Similarly, when an oscillator's frequency is multiplied, the integrated phase noise is in creased by the multiplication factor. At 10 GHz, for example, the integrated phase noise in the above example increases from 9 x 10-4 red to 0.9 rad! Such large phase excursions are detrimental to the performance of many systems, such as those which employ phase lock loops or phase-shift keying.
MEASUREMENT
The sidebands generated by vibration can be used to measure the acceleration sensitivity. Equation (15) can be rearranged to get
![]()
where ![]() is the component of the acceleration sensitivity vector in the i
direction. Three measurements, along mutually perpendicular axes, are required to
characterize
is the component of the acceleration sensitivity vector in the i
direction. Three measurements, along mutually perpendicular axes, are required to
characterize ![]() which becomes
which becomes
![]()
with a magnitude of
![]()
One scheme for measuring ![]() is shown in Fig. 7. The local
oscillator is used to mix the carrier frequency down to the range of the spectrum
analyzer. If the local oscillator is not modulated, the relative sideband levels are
unchanged by mixing. The frequency multiplier is used to overcome dynamic range
limitations of the spectrum analyzer, using the "20 log N" enhancement discussed
previously. The measured sideband levels must be adjusted for the multiplication factor
prior to insertion into (31). It must be stressed that (17) is valid only if
is shown in Fig. 7. The local
oscillator is used to mix the carrier frequency down to the range of the spectrum
analyzer. If the local oscillator is not modulated, the relative sideband levels are
unchanged by mixing. The frequency multiplier is used to overcome dynamic range
limitations of the spectrum analyzer, using the "20 log N" enhancement discussed
previously. The measured sideband levels must be adjusted for the multiplication factor
prior to insertion into (31). It must be stressed that (17) is valid only if ![]() < 0.1. A
sample measurement output and calculation is given in Fig. 8.
< 0.1. A
sample measurement output and calculation is given in Fig. 8.
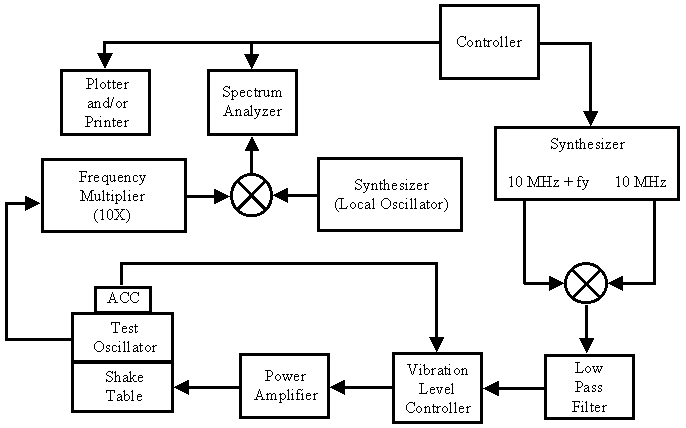
Fig. 7. Typical equipment configuration for measurement of acceleration-sensitivity using sinusoidal acceleration.
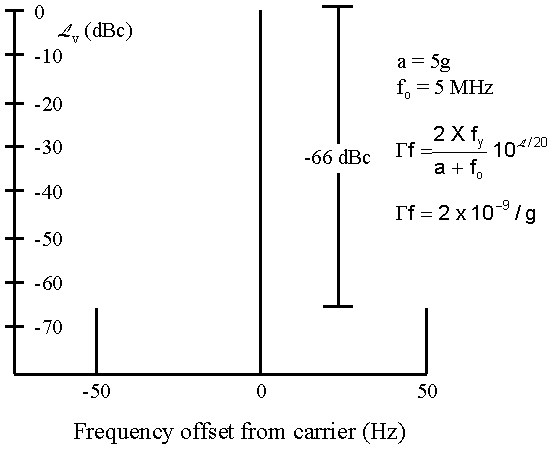
Fig. 8. Sample acceleration-sensitivity measurement using sinusoidal acceleration.
Other measurement schemes include passive excitation [17] of the resonator, the use of random vibration [18], and the 2-g tipover test. Many oven-controlled oscillators are not suitable for characterization by the 2-g tipover test, however, because rotation of the oscillator results in temperature changes inside the oven that can mask the effects due to the acceleration changes. Vibration tests are also subject to pitfalls since resonances in the oscillator or shake table assembly can produce false results. It is. therefore, important to perform the test at more than one frequency.
THEORY
The theoretical understanding of acceleration sensitivity does not yet enable one to predict the acceleration sensitivity of '`real" resonator designs. Theoretical activity started with the study of in-plane forces on simplified resonator models. The first studies were concerned with the closely related force-frequency effect. This effect, first reported by Bottom [19] in 1947, is the change in frequency induced by a pair of opposed forces in the plane of a resonator plate applied at the rim. Those forces distort the quartz plate and, because of the nonlinear elastic behavior, change the acoustic velocity [11]. Since the frequency of a resonator is a function of the acoustic velocity and the dimensions of the quartz plate, the forces change the frequency.
The first attempt at an analytical solution to the force frequency problem was made by Mingins, Barcus, and Perry in 1962 [20]. They assumed an AT-cut crystal plate of infinite lateral dimension and used a perturbation technique with linear elastic coefficients. In 1963, they discussed nonlinear theory and the need to include the third order elastic coefficients [21]. Those coefficients were measured in 1966 by Thurston, McSkimin, and Andreatch [22]. The first calculation to use the nonlinear theory was performed by Keyes and Blair in 1967 [23]. In 1973, Lee, Wang, and Markenscoff [24] published the first of a continuing series of papers (by Lee and his students), in which they calculated the force-frequency coefficient (as defined by Ratajski [25] as a function of azimuth, using the general theory of incremental elastic deformations superimposed on finite initial deformations. The next year, Lee et al. investigated the frequency change due to cantilever bending of the plate [26]. In 1977, a variational analysis of the force-frequency effect, including the effect of material anisotropy on initial stress, was given by EerNisse, Ballato, and Lukaszek [27] for doubly rotated cuts. In 1978, Janiaud, Nissim, and Gagnepain [28] obtained analytic solutions for the biasing stress in singly and doubly rotated plates subject to diametric forces. Those results allowed them to calculate Ratajski's force-frequency coefficient, and also the in-plane acceleration sensitivity. Lee and Wu [29] extended the work of [24] to treat plates of any cut. In that paper, the solution for an arbitrary number of ribbon supports was obtained.
Under acceleration, body forces in the quartz plate are balanced by reaction forces from the mounting structure. As in the force-frequency effect, distortion of the crystal lattice causes the resonant frequency to change. For bulkwave resonators, only the in-plane case has been treated. The first analysis was by Valdois, Besson, and Gagnepain [11] in 1974, who showed that the effect is linear. Several papers by Lee and Wu [29]-[31] considered resonators with three- and four-point mounts. Two-point mounts were considered by Janiaud, Nissim, and Gagnepain [28]. For SAW resonators, recent work by Shick and Tiersten [32] and by Sinha and Locke [33] has treated acceleration both in the plane of the plate and normal to it.
There seems to be a significant dependence of the acceleration sensitivity on small variations in the mounting. Analyses of bulkwave resonators, to-date, have considered only point supports. Real resonators have supports that are distributed over a finite area. In addition, initial stress conditions are difficult to determine and may not be well-reproduced. There is an ongoing effort by Lee and Tang [34] to use finite element analysis to more accurately model the mounting structure. It is hoped that this will allow computer simulations that will permit the determination of the optimum design parameters for minimizing acceleration sensitivity.
EXPERIMENTAL RESULTS
Several papers have reported experimental results on the force-frequency effect [20], [25], [35] and the effects of bending moments [36]. All used point mounts in special fixtures, and results agree fairly well with the theoretical analyses. The reported experimental observations of the actual acceleration sensitivity of real resonators, on the other hand, is remarkable in that it defies simple explanation. ,
The experimental effort on acceleration-sensitivity started in the 1960's with Smith, Spencer, and Warner [1]-[5]. Valdois, Besson, and Gagnepain [11] made measurements on resonators and oscillators to demonstrate that the resonator was the acceleration-sensitive element. Results from 2-g tipover experiments were reported for SC cut resonators by Kusters, Adams, Yoshida, and Leach [37] in 1977. In 1979, Warner, Goldfrank, Meirs, and Rosenfeld [38] reported results on SC- and FC-cut devices. In 1981, the first of a series of papers intended to explore a wide range of resonator fabrication parameters was published by Filler and Vig tam. In that same year, Nakazawa, Lukaszek, and Ballato [40] reported constant acceleration results that suggested an acceleration sensitivity that is not linear with acceleration level. The only significant parameter for the reduction of acceleration sensitivity was reported by Filler, Kosinski, and Vig [41] in 1982. As one makes piano-convex and biconvex AT-cut resonators flatter, the acceleration sensitivity decreases. It must be noted, however, that other effects, as yet undetermined, cause large scatter in the data. A survey of a large number of resonator parameters, such as SC-cut contour, thickness, drive level, temperature, and angle of cut, was published in 1983 by Filler, Kosinski, and Vig [42]. No significant correlations were found.
The most recent paper, by Weglein [43] in 1984, reported the acceleration sensitivity of VHF AT- and SC-cut resonators. All of the resonators in that study were disassembled after the acceleration sensitivity measurements to examine fabrication details. That investigation, which seems to summarize the efforts to date, showed "little dependence on any recognizable parameter," except that the lowest average acceleration sensitivity was found in the group of AT units. The large spread in the data, typical of all experimental observations of acceleration-sensitivity, seems to he caused by a combination of sometimes offsetting subtle effects, which are difficult to) control during fabrication.
REDUCTION OF THE ACCELERATION SENSITIVITY OF RESONATORS
The introduction of the stress-compensated cut of quartz, i.e., the SC-cut, was accompanied by the widespread expectation that the SC-cut would have significantly lower acceleration sensitivity than other cuts. Unfortunately, that expectation has not been realized. The lowest acceleration sensitivity achieved with AT-cut resonators [41]-[43] equals that achieved with SC-cut resonators; both cuts can have low parts in 1010/g sensitivity.
Efforts to reduce the sensitivity of individual resonators to the effects of acceleration have stressed the support structure. Lukaszek and Ballato [44] proposed a plate geometry that would assure the proper support configuration to reduce the force-frequency effect. Besson, Gagnepain, Janiaud and Valdois [45] proposed a support structure that insured symmetry with the median plane of the resonator plate. Debaisieux, Aubry, anal Groslambert [46] and Aubry and Debaisieux [47] have reported results using QAS resonators, a variation of the BVA [48], which insures symmetry of mount as well as accurate mount locations for reducing the force-frequency effect. Their results show a marked reduction in the scatter of the measured acceleration sensitivity.
ACCELERATION COMPENSATION OF OSCILLATORS
The lack of progress in reducing the acceleration sensitivity of the resonator below the low parts in 1010/g level has spawned several techniques for compensation of the effect. There are two general classes of compensation, passive and active. The first compensation results were published by Gagnepain and Walls in 1977 [49]. They used the passive method of mechanically arranging two resonators such that the components of the acceleration sensitivities normal to the plates were antiparallel. The resonators were electrically connected in series in a single oscillator. Przyjemski [12] and Emmons [50] used an active technique. They sensed the acceleration magnitude with an accelerometer aligned with the direction of the acceleration sensitivity vector of the resonator. The accelerometer signal was fed into a tuning circuit in the oscillator in order to counter the acceleration-induced frequency changes. A limitation of this technique is the requirement on the linearity of the tuning network at all operating points. Emmons also employed the dual-resonator technique and suggested using an acceleration-sensitive capacitor in the tuning network of the oscillator. The latter technique is available as an option on a commercial cesium-beam frequency standard.
Ballato [51] suggested a method for compensation in all directions using a resonator pair made of enantiomorphs. He argued that opposite handedness is the only way to have all three crystallographic axes line up antiparallel. This was extended by a series of patents by Ballato and Vig [52]-[54]. A simplification was patented by Filler [55], who showed that, since the acceleration-sensitivity has vector properties, all that is required is that the vectors be aligned antiparallel, independent of the handedness of the quartz. Vig and Walls [56] extended this work by suggesting a method to accommodate resonators with different acceleration sensitivity magnitudes.
Rosati patented [57] an active technique of compensation that was further developed by Rosati and Filler [58]. This method makes use of the polarization effect in doubly rotated resonators, i.e., that the resonant frequency of a doubly rotated resonator is a function of the voltage applied to the electrodes [59]. If one senses the acceleration using an accelerometer and feeds that signal with appropriate amplification and phase reversal directly to the resonator electrodes, compensation can be achieved. The advantage of feeding the correction signal to the resonator electrodes rather than a varactor is that the polarization effect has superior linearity. When the correction signal is applied to a varactor, the nonlinearity of the varactor and of the frequency-capacitance function causes sidebands at harmonics of the vibration frequency. One implementation of this technique was used to compensate a rubidium oscillator [60].
CONCLUSION
Vibration effects are a significant problem in modern communication, navigation, and radar systems. Progress has been made in understanding the causes of acceleration sensitivity but a full explanation for real devices has been elusive. A great deal of effort has been expended on compensating for acceleration-sensitivity, but more work is needed to improve the level and bandwidth of the compensation.
ACKNOWLEDGMENTS
For many helpful discussions, the author thanks Mr. Robert Smythe of Piezo Technology, Inc., and Dr. John Vig and Mr. Vincent Rosati of U.S. Army LABCOM. In addition, the author thanks Mr. Martin Bloch for generating the initial interest in this problem.
REFERENCES
[1] A. W. Warner and W. L. Smith, "Quartz crystal units and precision oscillators for operation in severe mechanical environments,''
14th Annu. Symp. Freq. Contr., 1960, pp. 200-216.
[2] W. L. Smith, "An ultra-precise standard of frequency," Final Report, Contract DA 36-039 sc-73078, U.S. Army, 1960.
[3] W. J. Spencer and W. L. Smith, "Precision crystal frequency standards," 15th Annu. Symp. Freq. Contr., 1961, pp. 139-155.
[4] --"Precision quartz crystal controlled oscillator for severe environment conditions,'' 16th Annu. Symp. Freq. Contr., 1962. pp. 406
-421.
[5] W. L. Smith and W. J. Spencer, "Quartz crystal controlled oscillators," Final Report, Contract DA 36-039 sc-85373, U.S. Army.
1963.
[6] D. B. Leeson, "Aerospace crystal environmental requirements,'' 19th Annu. Symp. Freg. Contr., 1965, pp. 49-57.
[7] D. B. Leeson and G. F. Johnson, "Short-term stability for a Doppler radar: Requirements, measurements, and techniques," in Proc. IEEE, 54, 1966, pp. 244-248.
[8] G. F. Johnson, "Vibration characteristics of crystal oscillators," 21st Annu. Symp. Freq. Contr., 1967, pp. 287-293.
[9] J. Moses, "NAVSTAR global positioning system oscillator requirements for the GPS manpack,'' 30th Annu. Symp. Freq. Contr.,
1967, pp. 390-400.
[10] J. M. Przyjemski and P. L. Konop, "Limitations on GPS receiver performance imposed by crystal-oscillator g-sensitivity," NAECON '77, 1977.
[11] M. Valdois, J. Besson, and J. J. Gagnepain, "Influence of environment conditions on a quartz resonator," 28th Annu. Symp. Freq.
Contr., 1974, pp. 19-32.
[12] J. M. Przyjemski, "Improvement in system performance using a crystal oscillator compensated for acceleration sensitivity," 32nd
Annu. Symp. Freq. Contr., 1978, pp. 426-431.
[13] M. Abramowitz and I. A. Stegun, "National Bureau of Standards, Applied Mathematics Series, No. 55," Government Printing Office, Washington, DC, 1964; revised by Dover, New York, 1965.
[14] R. L. Filler, "The effect of vibration on frequency standards and clocks," 35th Annu. Symp. Freq. Contr., 1981, pp. 31-39.
[15] S. Stein, private communication, 1986. Using Eq. 23 from Barnes et al., ''Characterization of frequency stability," IEEE Trans.
Instrum. Meas., vol. IM-20, pp. 105-120, May 1971.
[16] D. Halford, J. S. Shoaf, and A. S. Ris!ey, "Spectral density analysis: Frequency domain specification and measurement of signal
stability,'' 27th Annu. Symp. Freq. Contr., 1973, pp. 421-431.
[17] F. L. Walls and A. E. Wainwright, "Measurement on the short-term stability of quartz crystal resonators and the implication for crystal
oscillator design," IEEE Trans. Instrum. Meas., vol. IM-24, pp. 15-20, 1975.
[18] D. J. Healy III, H. Hahn, and S. Powell, "A measurement technique for determination of frequency versus acceleration
characteristics of quartz crystal units," 37th Annu. Symp. Freq. Contr., 1983, pp. 284-289.
[19] V. Bottom, "Note on the anomalous thermal effect in quartz oscillator plates," Amer. Mineralogist, vol. 32, pp. 590-591, Sept.-Oct.
1947.
[20] C. R. Mingins, L. C. Barcus, and R. W. Perry, "Effects of external forces on the frequency of vibrating crystal plates," 16th Annu.
Symp. Freq. Contr., 1962, pp. 47-76.
[21] C. R. Mingins, L. C. Barcus, and R. W. Perry, "Reactions of a vibrating piezoelectric plate to externally applied forces,'' 17th Annu.
Symp. Freq. Contr., 1963, pp. 51-87.
[22] R. N. Thurston, H. J McSkimin, and P. Andreatch, Jr., "Third-order elastic coefficients of quartz," J. Appl. Phys., vol. 37, pp.
267-275, Jan. 1966.
[23] R. W. Keyes and F. W. Blair, "Stress dependence of the frequency of quartz plates, ' ' Proc. IEEE (letters), 1967, pp. 565-566.
[24] P. C. Y. Lee, Y. S. Wang, and X. Markenscoff, "Elastic waves and vibrations in deformed crystal plates," 27th Annu. Symp. Freq.
Contr., 1973, pp. 1-6.
[25] J. M. Ratajski, "The force sensitivity of AT-cut quartz crystals," 20th Annu. Symp. Freq. Contr., 1966, pp. 33-48.
[26] P. C. Y. Lee and Y. S. Wang, ''Effects of initial bending on the resonance frequencies of crystal plates,'' 28th Annu. Symp. Freq.
Contr., 1974, pp. 14-18.
[27] E. P. EerNisse, T. Lukaszek, and A. Ballato, "Variational calculations of force-frequency constants of doubly rotated quartz
resonators," IEEE Trans. Sonics Ultrason., vol. SU-25, no. 3, pp. 132-138, May 1978.
[28] D. Janiaud, L. Nissim, and J. J. Gagnepain, "Analytical calculation of initial stress effects on anisotropic crystals application to
quartz resonators," 32nd Annu. Symp. Freq. Contr., 1978, pp. 169-179.
[29] P. C. Y. Lee and K. M. Wu, "Nonlinear effect of initial stresses in doubly-rotated resonator plates," 34th Annu. Symp. Freq. Contr.,
1980,pp.403-4ll.
[30] --, "Effects of acceleration on the resonance frequencies of crystal plates," 30th Annu. Symp. Freq. Contr., 1976, pp. 1-7.
[31] --, "The influence of support configuration on the acceleration sensitivity of quartz resonator plates," 31st Annu. Symp. Freq. Contr.,
1977, pp. 29-34.
[32] D. V. Shick and H. F. Tiersten, "An analysis of the acceleration sensitivity of ST-cut quartz surface wave resonators supported
along the edges," 40th Annu. Symp. Freq. Contr., 1986, pp. 262-268.
[33] B. K. Sinha and S. Locke, ''Acceleration and vibration sensitivity of SAW devices,'' IEEE Trans. Ultrason. Ferroelec. Freq. Contr.,
vol. UFFC-34, no. 1, pp. 29-38, Jan. 1987.
[34] P. C. Y. Lee and M. S. H. Tang, "Initial stress field and resonance frequencies of incremental vibrations in crystal resonators by
finite element method," 40th Annu. Symp. Freq. Contr., 1986, pp. 152-160.
[35] A. D. Ballato, "Effects of initial stress on quartz plates vibrating in thickness modes," 14th Annu. Symp. Preg. Contr., 1960, pp.
89-114.
[36] E. D. Fletcher and A. J. Douglas, "A comparison of the effects of bending moments on the vibrations of AT and SC (or TTC) cuts of
quartz," 33rd Annu. Symp. Freq. Contr., 1979, pp. 346-350.
[37] J. A. Kusters, C. A. Adams, H. Yoshida, and J. G. Leach, "TTC's - Further developmental results," 31st Annu. Symp. Freq. Contr.,
1977, pp. 3-7.
[38] A. Warner, B. Goldfrank, M. Meirs, and M. Rosenfeld, "Low 'g' sensitivity crystal units and their testing," 33rd Annu. Symp. Freq.
Contr., 1979, pp. 306-310A.
[39] R. L. Filler and J. R. Vig, ''The acceleration and warmup characteristics of four-point-mounted SC and AT-cut resonators," 35th
Annu. Symp. Freq. Contr., 1981, pp. 110- 116.
[40] M. Nakazawa, T. Lukaszek, and A. Ballato, "Force- and acceleration-frequency effects in grooved and ring-supported resonators,''
35th Annu. Symp. Freq. Contr., 1981, pp. 71-91.
[41] R. L. Filler, J. A. Kosinski, and J. R. Vig, "The effect of blank geometry on the acceleration sensitivity of ATand SC-cut quartz
resonators," 36th Annu. Symp. Freq. Contr., 1982, pp. 215-219.
[42] --, "Further studies on the acceleration sensitivity of quartz resonators," 37th Annu. Symp. Freq. Contr., 1983, pp. 265-271.
[43] R. D. Weglein, "The vibration sensitivity of VHF quartz crystals for missile applications," 38th Annu. Symp. Freq. Contr., 1984, pp.
73-79.
[44] T. J. Lukaszek and A. Ballato, "Resonators for severe environments, " 33rd Annu. Symp. Freq. Contr., 1979, pp. 311-321 .
[45] R. Besson, J. J. Gagnepain, D. Janiaud, and M. Valdois, "Design of a bulk wave quartz resonator insensitive to acceleration,'' 33rd
Annu. Symp. Freq. Contr., 1979, pp. 37-345.
[46] A. Debaisieux, J . P. Aubry, and J. Groslambert, " Design of SC cut 10 MHz H.Q. crystals with g sensitivity better than 2.10-10/g," in
Proc. 15th PTTI Conf., 1983, pp. 635-650.
[47] J. P. Aubry and A. Debaisieux, "Further results on 5 MHz and 10 MHz resonators with BVA and QAS designs,'' 38th Annu. Symp.
Freq. Contr., 1984, pp. 190-200.
[48] R. J. Besson, ''A new piezoelectric resonator design,'' 30th Annu. Symp. Freq. Contr., 1976, pp. 78-83.
[49] J. J. Gagnepain and F. L. Walls, "Quartz crystal oscillators with low acceleration sensitivity," NBSIR 77-855, National Bureau of
Standards, 1977.
[50] D. A. Emmons, "Acceleration sensitivity compensation in high performance crystal oscillators," 10th PTTI Conf., 1978.
[51] A. Ballato, "Crystal resonators with increased immunity to acceleration fields,'' IEEE Trans. Sonics Ultrason., vol. SU-27, no. 4, pp.
195-200, July 1980.
[52] A. Ballato and J. R. Vig, "Acceleration resistant combination of opposite-handed piezoelectric crystals," U.S. Patent No. 4,344,010,
1982.
[53] --, ''Method of fabricating acceleration resistant resonators, resonators so formed," U.S. Patent No. 4,365,182, 1982.
[54] A. Ballato and J. R. Vig, ''Method of fabricating acceleration resistant crystal resonators," U.S. Patent No. 4,409,711, 1983.
[55] R. L. Filler, ''Acceleration resistant crystal resonators," U.S. Patent No. 4,410,822, 1983.
[56] J. R. Vig and F. L. Walls, "Acceleration insensitive oscillator," U.S. Patent No. 4,575,690, 1986.
[57] V. J. Rosati, "Suppression of vibration effects on piezoelectric crystal resonators," U.S. Patent No. 4,453,141, 1984.
[58] V. J. Rosati and R. L. Filler, "Reduction of the effects of vibration on SC-cut quartz crystal oscillators," 35th Annu. Symp. Freq.
Contr., 1981, pp. 117- 121.
[59] J. Kusters, "The effect of static electric fields on the elastic constants of alpha quartz," 24th Annu. Symp. Freq. Contr., 1970,
pp. 46-54.
[60] C. Colson, "Vibration compensation of the seektalk rubidium oscillator,'' 36th Annu. Symp. Freq. Contr., 1982, pp. 197-199.
 Raymond L. Filler (M'75) was born in Brooklyn,
NY, in 1948: He received the B.S. degree in physics from Rensselaer Polytechnic Institute,
Troy, NY, in 1969 and the Ph.D. degree from Rutgers, New Brunswick, NJ, in 1975.
Raymond L. Filler (M'75) was born in Brooklyn,
NY, in 1948: He received the B.S. degree in physics from Rensselaer Polytechnic Institute,
Troy, NY, in 1969 and the Ph.D. degree from Rutgers, New Brunswick, NJ, in 1975.
He is currently the leader of the Crystal Resonator Team of the Frequency Control and Timing Branch of the Electronics Technology and Devices Laboratory (LABCOM), Fort Monmouth, NJ. His research interests include techniques to improve long and short term stability, and shock and vibration sensitivity of quartz crystal resonators. He has five patents in the frequency control field.
Dr. Filler is a member of the American Physical Society. He has served as the Publicity Chairman of the IEEE co-sponsored Annual Symposium on Frequency Control since 1986, and as Chairman of a committee to establish traceability of crystal parameter measurement to the National Bureau of Standards.