Methods

DC Resistivity

    Electromagnetic properties of the ground are expressed by their resistivities (W m) or conductivities (mS/m), which are inversely related. Conductivity in the ground is dominated by electrolytic interactions mediated by water, whose salinity affects conductivity within pore spaces. Geoelectrical methods, like most geophysical methods, detect contrasts rather than absolute values of physical properties.
    Direct current (DC) resistivity methods involve the introduction of DC signals (I) into the ground at current electrodes (A and B) and measurement of the resulting potential difference (V) at the potential electrodes (M and N). Usually this is repeated 8 to 12 times to increase the signal to noise ratio. Dipole-dipole and Schlumberger arrays were used on Sapelo Island.
    A 20 m long dipole-dipole survey was conducted perpendicular to the creek, beginning approximately 20 m from the creek bank (across the access road) and running north. The measured, or apparent, resistivity (r_app ) is at a point assumed to apply halfway between AB and MN and at a depth equal to half the distance between AB.

(Eq 1)

n is number of times MN has been moved away from AB, and a is the constantly held distance between AB and MN. Making a 1 meter and the array 20 m long, finding the water table and the freshwater/saltwater interface was expected. To image the geoelectrical structure, data are used to create 2 dimensional maps superimposed with apparent resistivity.
    Schlumberger arrays are used to describe lateral variations and depth of layers. To describe the 2 dimensional variations of the water table at Kenan Field we conducted a Schlumberger array that was parallel to the creek and about 150 m away. In a Schlumberger array, A and B are outside of M and N, and the center of the array is held constant. A and B were moved out in a standard logarithmic fashion. M and N are also moved out from the center in order to maintain the AB/MN ratio. After apparent resistivity is plotted and normalized, the resulting curve can be interpreted in terms of resistivity structure using standard curve comparison.

(Eq 2)

AB/2 and MN/2 are half the distance between A and B and M and N, respectively.

Terrain Conductivity

    The EM-31 introduce AC current into the ground at a receiver and measure a response that is a function of the conductive/resistive structure. The EM-31 uses a coiled loop transmitter oriented as a horizontal or vertical dipole, depending on the survey, that produces a primary magnetic field (H_p) to induce current into the ground. The field propagates and produces a potential difference, or voltage (V), in a conductive body. The voltage in the conductor produces an induced current in the conductive body, which generates a new, secondary, magnetic field (H_s). The receiver measures the secondary field, and apparent conductivity is calculated using the ratio of the primary and secondary magnetic fields.

w is the angular frequency and m₀ is the permeability of free space.
    Transmitter-receiver spacing, frequency of the signal, and the conductivity of the ground determines depth of penetration. For the EM-31 the average penetration depth is 6 m and the radius of investigation is 3 m (Milsom p. 108). This depth is sufficient to encounter the water table. There were two EM-31 survey lines on Sapelo Island, one perpendicular to the creek (along the dipole-dipole array) and one parallel to the creek (along the seismic line and Schlumberger array). We recorded quadrature phase data (i.e. the real component of apparent conductivity which gives the Hs/Hp ration) using both horizontal and vertical dipoles. The EM-31 was operated both perpendicular and parallel to the survey lines. Models are made using apparent conductivity and inversions of the following equations for two and three layers, respectively.
    For the two layer model, apparent resistivity is:

    For the three layer model, apparent resistivity is:

Both models use:

where s₁,s₂, and s₃ are the conductivities of the three layers (with the lowest layer being a halfspace), z is the depth to respective layer, z' is the ratio of z to the intercoil spacing, and R_v(z) and R_h(z) are the instrument response functions for the vertical and horizontal dipole orientation, respectively.
 

Data

DC Resistivity
    Schlumberger array data are plotted in Figure 1. There are no general trends in the data. Multiple measurements made with constant spacing resulted in values that disagree by up to three orders of magnitude.
    Dipole-dipole data are plotted in Figure 2. Apparent resistivities range from 6 to 5500 W m. Resistivity decreases with depth. The average apparent resistivity is approximately 1500 W m. Lateral variations within the first four meters are less than those at depth. At 5 and 8 m depth some data points have values significantly lower than the others.

Terrain Conductivity
    Raw data collected from terrain conductivity measurements, adjusted to compensate for highly conductive environments, are plotted in Figure 3 and Figure 4.
The data are adjusted using:

for the vertical dipole mode and apparent conductivities up to 300 mS/m and

for the horizontal dipole mode and apparent conductivities up to 250 mS/m. In Figure 3 the apparent conductivity decreases dramatically within 20 meters of the creek and then levels off to a relatively consistent value. The apparent conductivity range is from 27 to 152 mS/m with a mean value of 27 and 35 mS/m for the vertical and horizontal dipole orientations, respectively. Apparent conductivity values are approximately 8 mS/m higher for the data collected in June than those collected in October. In Figure 2 the trend is more linear, that is the conductivity ranges from only 27 to 31 mS/m. As in Figure 1, apparent conductivities are consistently higher in June than in October. At the well transect (i.e. 0 m), all of the data shift to a higher value by about 2 mS/m. It should be noted, however, that the position of the survey line of the data collected in June is not known and is plotted where it is it assuming the similar increase occurs at the same place.
 

Results

DC Resistivity

    The Schlumberger data (Figure 3) do not show decreasing resistivity with depth as do EM-31 and dipole-dipole resistivity data. Site selection, which is extremely important in all sounding work, is particularly critical with the Schlumberger array, because it is very sensitive to conditions around the closely spaced inner electrodes. A location where the upper layer is very heterogeneous is unsuitable for an array center. [Milsom page 89] Indeed, EM-31 data collected along the Schlumberger array do show heterogeneity (see Figure 4).
    The average depth to the water table using water level measurements in the wells was 2.2 m. The Figure 2 shows linearly varying apparent resistivities from approximately 5000 to 1000 W m in the first 3 m. At 2.2 m depth on the pseudo-section the apparent resistivity is approximately 2000 W m. This value falls within the range for sand saturated with freshwater (Reference). Apparent resistivity between 3 and 8 m depth varies from approximately 1000 to 100 W m. These values also fall within the range of sand saturated with freshwater (reference). Below 8 meters the resistivity varies from 700 to only 6 W m, which suggests some of the sand may be saturated with seawater at these depths. Below 4 meters, resistivity does not appear to be as uniform with depth in the shallowest 4 meters. Starting at 4 m depth and 8.5 m from the road, there is a "finger" of high resistivity relative to other points at corresponding depths, that extends away from the road dipping down at an angle of 45 degrees. This may be the effect of a thin dipping layer that has a higher resistivity than the surrounding layers. It could also be the effect of a region of high resistivity near the electrodes at the surface. However, at shallow depths there are no significant lateral variations. It was noted during the survey that there were problems with the instrument/electrode contacts while sampling at the points in question. This may account for the high resistivities since poor contact reduces inductance and thus would cause apparent resistivities to be higher.

Terrain conductivity

    For the two and three layer models, the resistivity of the first layer is assumed to be greater than 100 W m (see dipole-dipole pseudo section). Figure 5 quantifies the sensitivity of the model to layer 2 resistivities. Figure 6 shows in the two layer model that for layer 1 resistivities above 100 W m the resistivity of layer 2 asymptotically reaches 15 W m (67mS/m) for the horizontal dipole survey data and 9 W m (111mS/m) for the vertical dipole survey data. The three layer model was used primarily to find the depth to the third layer, i.e. the saltwater/freshwater interface. The depth assigned to the first layer was 2.2 m, the resistivity for the first layer was chosen to be 3500 W m (figure dipole), the resistivity used for the second layer was 169 W m taken from CST data, and 10 W m for the third layer. Like the two layer model, the three layer model is very insensitive to layer 1 resistivities. The depth to the third layer, presumably the freshwater/saltwater interface is calculated to be 15.6 m.

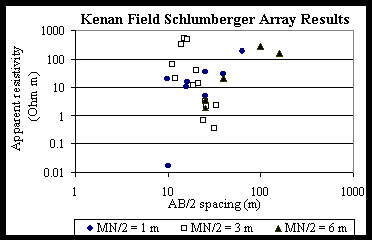
        Figure1  Plot of raw Schlumberger data.

Figure 2
 
 
 

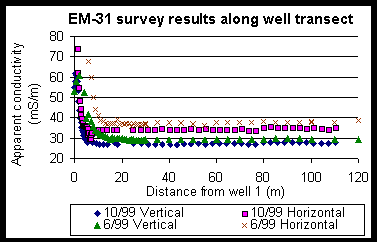(Figure 3)
        Figures 3 and 4 Plots of adjusted raw terrain conductivity data collected from surveys using the EM-31 at Kenan Field perpendicular and parallel to the tidal creek.  Vertical and Horizontal refer to dipole orientations, and along and perpendicular refer to the orientation of the instrument relative to the survey line.  6/99 and 10/99 refer to data collected during a previous survey conducted in June 1999 and one in October 1999 by the EAS 4420 class, respectively.  In Figure 4 the data collected in June 1999 were along a line approximately 150 meters away from the tidal creek and the collected by the 1999 EAS 4420 class were along a line approximately 120 m from the tidal creek.
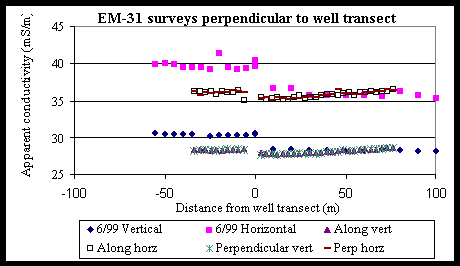(Figure 4)
 

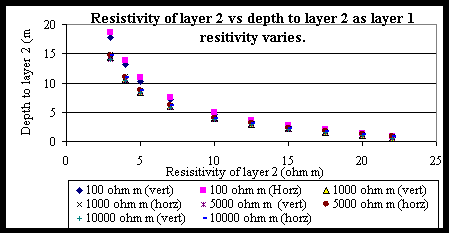
        Figure 5  Plot that shows how the second layer is highly sensitive to varying layer 2 resistivities and practically negligent to varying layer 1 resistivity.

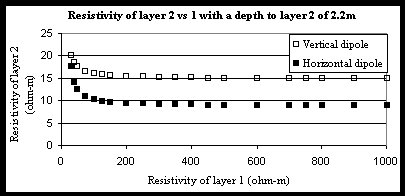
        Figure 6  Plot that shows layer 1 and 2 conductivity values that yield a depth of 2.2 m to the first layer according to equations 4 and 5.