On-Axis Field Due to a Current Loop
| This simple formula uses the law of Biot Savart, integrated over a circular current loop to obtain the magnetic field at any point along the axis of the loop. | |
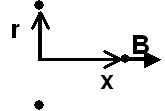 Current loop in cross section view. |
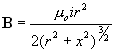 B is the magnetic field, in teslas, at any point on the axis of a current loop. The direction of the field is perpendicular to the plane of the loop.
i is the current in the wire, in amperes. r is the radius of the current loop, in meters. x is the distance, on axis, from the center of the current loop, in meters. |
| Special
Case: x = 0
|
|
| Special
Case: x >> r
Note that this is equivalent to the expression for on axis magnetic field due to a magnetic dipole:
where A is the area
of the current loop, or |
|
is the permeability constant
(1.26x10-6 H/m)
