| Off-Axis Field Due to a Magnetic Dipole Moment |
![]()
| At points far from a magnet, solenoid, current loop or Helmholtz coil, you can approximate the field by modeling the coil (or magnet) as a magnetic dipole moment. The error of this technique is less than roughly 2% at distances greater than 5 times the largest dimension of the coil (or magnet), and it approaches 0% as the distance approaches infinity. | |
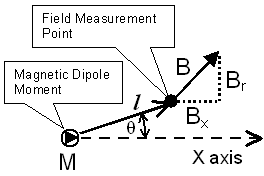 |
|
| B
is the magnetic field, in teslas, at any point in space
that isn't at the origin. It is equal to the sum of two
field components, BX the magnetic field component which is aligned with the x axis and Br the magnetic field component which is in a radial direction. x is the distance, on axis, from the dipole to the field measurement point, in meters. l is the distance from the dipole to the field measurement point, in meters. q is angle between the dipole axis, and the position vector of the field measurement point. |
|
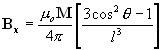
|
|
| where, M is the strength of the magnetic dipole moment, in ampere meters squared (Am2). m o is the permeability constant (1.26x10-6 H/m or 4p x10-7) As always, units of linear dimension (l) and magnetic field (B) are adjustable by using an appropriate value for the permeability constant. |
|
Magnetic Dipole Moment |
A
magnetic dipole moment is a simple mathematical
representation of a coil, electromagnet or permanent
magnet ("refrigerator magnet") that can be used
to predict the magnetic field at a distance from its
source. The prediction is generally accurate only if the
distance to the measurement point is much greater than
the largest dimension of the magnet. For example, the error is roughly less than 2% for distances greater than 5 times the largest magnet dimension. For air core electromagnets,
where, N is the number of turns of wire in the magnet, i is the current in the coil, in amperes, and A is the mean area of the coil, in meters squared (m2). For permanent magnets, magnetized in a single direction,
where, Bi is the "intrinsic induction" of the magnet, in teslas, V is the volume of the magnet, in meters cubed (m3). |
How do I figure out what Bi is? |
For
many fully magnetized rare earth (Neodymium Iron Boron or
Samarium Cobalt) ceramic or ferrite magnets, Bi
is approximately equal to Br, which is available from the
magnet manufacturer. For Alnico magnets, Bi is
approximately equal to Br only if the magnet's
length to width ratio (magnetized lengthwise) is much
greater than 1. Typical values for Br are: 0.4 teslas for ceramic or ferrite magnets, 1.0-1.5 teslas for Alnico and rare earth magnets. |
| Predicting
the field due to a dipole moment based on a single field
measurement on axis. If you can make a single, on axis, field measurement at some distance (greater than 5X magnet size) from a magnet, then you can predict the field at any point in space surrounding the magnet. |
|
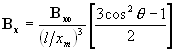
|
|
| where, Bxo is the measured field strength at some point, xm meters from the center of the magnet and on its axis. |
|
![]()