Off-Axis Field Due to a Current Loop
This simple formula can be obtained using the law of Biot Savart, integrated over a circular current loop to obtain the magnetic field at any point in space. Compare this to the much simpler formula for calculating the on-axis magnetic field due to a current loop.
  B is the magnetic field, in teslas, at any point in space that isn't on the current loop. It is equal to the sum of two field components,

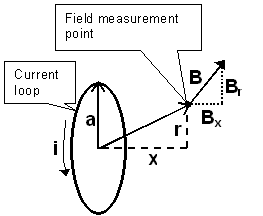
BX the magnetic field component which is aligned with the coil axis and

Br the magnetic field component which is in a radial direction.

i is the current in the wire, in amperes.

a is the radius of the current loop, in meters.

x is the distance, on axis, from the center of the current loop to the field measurement point, in meters.

r is the radial distance from the axis of the current loop to the field measurement point, in meters.
 

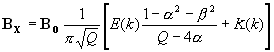
and
   
  where,

,

,

,

,

,

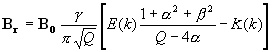
K(k) is the complete elliptic integral function, of the first kind.

E(k) is the complete elliptic integral function, of the second kind.

Note that the argument to K and E is shown here as the modulus "k". Other valid arguments are the parameter "m" (where m = k2) and the modular angle "a" (where a = sin-1k). Substitute the argument that is appropriate for the mathematical tool you are using.

is the magnetic field at the center of the coil, in teslas, and

m o is the permeability constant (1.26x10-6 H/m or 4p x10-7)

As always, units of linear dimension (a) and magnetic field (B) are adjustable by using an appropriate value for the permeability constant.

"Uh Oh"

Elliptic Integrals?

 "What is an elliptic integral function?" you say. My calculator doesn't have one of those!

If you want to use the formulas on this page, you'll need to be able to find complete elliptic integrals of the first and second kind for values of k between 0 and 1:

Download a copy of Expression Calculator from Vestris Inc. This powerful scientific calculator program includes a variety of elliptic integral functions.

Write your own program (in a spreadsheet macro, programmable calculator, or high level language) to compute elliptic integrals. You are free to look at some sample source code (written in C), which also includes a short program for computing the magnetic field due to a current loop.

Or you can look it up in a book of obscure math tables, like the CRC Standard Mathematical Tables and Formulae.

Or you can use (and peruse a JavaScript source code of) this calculator for computing off axis fields due to a current loop.
   

"Wait a second... "

 "I thought this web site had something to do with magnet design without computers. What gives?"

You don't have to use a computer to use the formulas on this page. Just grab your trusty slide rule and your table of elliptic integrals and go to work!

Actually, the true intent of this web site is to cover methods that don't involve Finite Element Analysis or its kin. FEA is extremely compute intensive and, in my opinion, tends to obscure the modest elegance of magnetics and the underlying relationships between current, power, permeability and size.

Credits

 The formulas on this page are adapted from:

SOME USEFUL INFORMATION FOR THE DESIGN OF AIR-CORE SOLENOIDS by D.Bruce Montgomery and J. Terrell., published November, 1961, under Air Force Contract AF19(604)-7344.

Montgomery and Terrell, in turn, credit:

STATIC AND DYNAMIC ELECTRICITY by W.R. Smythe, p. 266, McGraw-Hill, New York, 1950.

Magnet Formulas HOME | E-mail

Last updated: 10/28/2000

 

 

 

1