A popular and sensible approach to experimental design is to take a structure that is representative of the target you are trying to study in the field, generate synthetic data by forward modelling, and then invert the synthetic data to discover how well the original structure is recovered. Occam's inversion is ideal for this sort of study, as it does not depend on a priori starting models, and it will not include any structure not intrinsically resolved by the data you have generated.
There is one common pitfall in this process:
Many people fail to corrupt the synthetic data with synthetic noise, adding only error bars but no error. After all, accurate data is bound to give better results than noisy data, right? Wrong!!
Before I explain why it bad to generate accurate synthetic data and pretend that it includes noise instead of actually adding noise, let me show you a result:

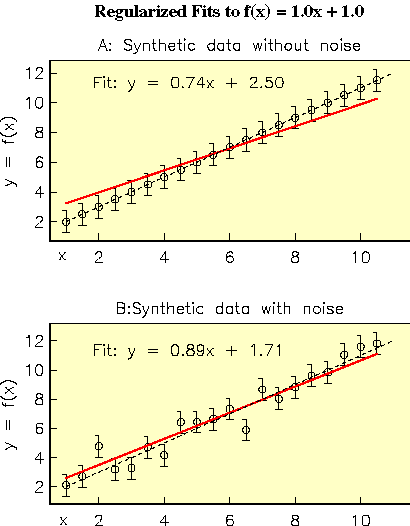
In the above pictures, data were generated from the underlying model f(x) = 1.0x + 1.0 and the data inverted with a linear version of Occam which penalized slope. Error bars were set at 0.75 (absolute error) and the target misfit was RMS 1.0. If errors are not added, the misfit budget is used to reduce the slope to 0.74. When error is added, part of the misfit budget has to be used to accommodate the noisy data, and now the inverted slope of 0.89 is much closer to the true value of 1.0.
In a classic least squares approach, failure to add noise to synthetic data usually makes little difference to the outcome, although data without noise can sometimes be fit exactly by an inversion algorithm. (Since this is rarely the case for a realistic data set, one might argue against using noise-free data even here as well). However, in an extremal (Occam) inversion the result will always be biased if noise is omitted, and the results are usually better when noise is added. Not only is the model penalised more than would be the case if the misfit budget was spent accommodating the variations in data, but the data residuals will also be serially correlated, violating assumptions about properties of data noise, including the use of the expected value for chi-sqaured.
In conclusion, failure to add noise to computed data in synthetic model studies not only fails to provide a realistic test of inversion algorithms, but in extremal inversions will bias the result significantly. The bias is in a direction which reduces the apparent resolving power of the experiment being modelled.
More information can be obtained by reading:
Constable, S.C., 1991: Comment on `Magnetotelluric appraisal using simulated annealing' by Dosso and Oldenburg, Geophys. J. Int., 106, pp. 387-388.