Radar
Echoes From the Moon
January 1946
By Jack Mofenson,
Evans Signal Laboratory, Belmar N.J.
|
Detailed
description of the techniques underlying the first
recorded radio transmission through outer space.
Calculations show that the maximum range of the Signal
Corps radar on lunar target exceeds one million miles
|
 Dr. Harold T. Webb (right)
adjusts the auxiliary tuning crystal in the lunar
receiver while E. K. Stodola looks on. Behind Stodola is
the nine-inch type-A indicator which records the echoes.
|
THE RECENT
EXPERIMENTS performed
by the Signal Corps Engineering Laboratories in receiving
radar echoes from the moon have aroused much
comment from engineers, astronomers and others engaged
in technical pursuits. Although the scientific aspects of
sending radio-frequency signals through the
ionosphere are certainly of importance, the work done on
the project is better classified as an
engineering achievement. As yet, no long-term
systematic observations have been made. This article is
confined, therefore, to a discussion of the
technical characteristics and general description of
the equipment employed. Briefly, the
experiment consisted of transmitting
quarter-second pulses of radio-frequency energy at 111.5
mc every four seconds in the direction of the
moon, and detecting echo signals approximately 2.5 seconds
after transmission. Display of the detected
signals was audible as well as visible.
Technically, the experiment utilized
well-established radar techniques, but with
radically different constants throughout the
system. Considerations of pulse width,
receiver bandwidth, transmitter power and the precise
frequency of the returned signal due to Doppler
effect, were such that careful attention had to
be given to the design of the overall equipment.
After preliminary calculations were made
concerning transmitter power, the reflectivity
coefficient of the target, and receiver noise
figure, it was apparent that receiving radar
echoes from the moon was technically possible. Under
the direction of Lt. Col. John H. DeWitt, a project
called "project Diana" was set up in
September 1945 to develop a radar system capable of transmitting
r-f pulses to the moon, and detecting echoes
more than 2 seconds later. Prior to entering the
Signal Corps, Colonel DeWitt, who at that time was
chief engineer of Radio Station WSM in
Nashville, Tenn., designed and constructed transmitting
and receiving equipment for the purpose of receiving
echoes from the moon. This equipment employed
substantially similar transmitter power and
frequency to that used by the Signal Corps,
but the attempt was a failure due to
insufficient sensitivity in the receiver. Colonel
DeWitt's appreciation of the problem and personal supervision
were the driving forces that made the present
experiment successful. Assisting Lt. Colonel
DeWitt were: E. K. Stodola, Dr. Harold D.
Webb, Herbert P. Kauffman and the writer, all of Evans
Signal Laboratory. Credit is also due the
members of the Antenna and Mechanical Design
Croup, Research Section, Theoretical Studies Group
and others.
The practical implications of radar
contact with the moon are numerous. During the
war the Germans used the V2 Rocket which climbed
some 70 miles above the earth, and the future
holds the unhappy prospect of missiles going far higher
than this. The matter of transmission of radio
signals to great distances above the earth for
detection and control of such weapons becomes a
problem of military importance. Further, the use
of a reflector far beyond the earth for radio
waves makes possible direct measurement of the
ability of radio waves to penetrate the
ionosphere. A more complete investigation in
this direction is indicated. The possibility of
using the moon as the reflector for a part-time
long-distance point-to-point communication system is also
being considered, as well as using the moon
as a target to measure field strength patterns.
|
 Lt. Colonel John H. DeWitt Jr., in charge of the
project, a modified version of the SCR-271 early-warning
radar used at Pearl Harbor. DeWitt is the former chief
engineer of WSM.
|
 The
author, Jack Mofenson, adjusts the position of the
waveform-monitoring stub. Over this transmission line
traveled the 3-kw transmitted pulse and a millionth of a
billionth watt echo.
|
Determination of Requirements
Several of the constants which determine the
maximum distance at which a radar set can detect targets
are peak transmitter power, radio-frequency of the
transmitted signal, duration of the signal, receiver
noise figure, and target echoing area. These
constants, among others, are concisely summarized in
what has been called the free-space radar equation.
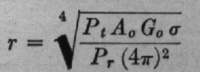 Equation (1)
Equation (1)
This equation has already been derived in Electronics In
this equation, r is
the radar range at which a signal may be detected, Pt
is the transmitter power during the pulse, Go,
the transmitting antenna power gain, A. the absorption
area of the receiving antenna, o
the effective echoing area of the target, and P,
the power of a barely discernible signal, on the
same basis as Pt.
The power gain due to ground reflections (not considered
in the freespace equation) at maximum effectiveness increases the
range of the system by a factor of 2. This is equivalent
to a power gain of 12 db. In the case of a target as
large as the moon (2160 miles diameter), calculations
showed that in order to receive an echo from the whole
hemisphere of the moon at once a pulse width greater
than 0.02 seconds was required. This set a lower limit
on the transmitter pulse width which corresponds to an
optimum bandwidth of 50 cps for the receiver. These
requirements eliminate, for the present, the use of the microwave
frequencies, because of considerations of pulse length.
 Propagation studies indicated
that electromagnetic waves at a frequency of
110 mc were capable of penetrating the ionosphere, and because of
availability of equipment, a radar set operating at 111.5 me
was chosen for the experiment. The peak power available
in this transmitter was equivalent to 3000 watts for
Pt
using a 0.25-second pulse. The transmitter had
the added advantage of being crystal controlled,
deriving its final radio frequency after a series of
frequency multiplication from a 516.2-kc crystal oscillator. The
receiver associated with the transmitter was of
the multi-mixer type (quadruple superheterodyne) capable
of beating down radio-frequency signals to a final
intermediate frequency of 180 cycles per second. Such an
arrangement permitted use of an extremely narrow pass
band, 57 cps, thus making the receiver highly selective and limiting
the noise to a very low value. The extremely narrow-band
receiver was an advantage, also, because it permitted tuning the
receiver to the exact radio frequency of the returned
echo. The importance of this can best be realized by
considering the fact that due to the relative velocities of the
earth and the moon, the returned signal may differ from
the transmitted signal by as much as 300 cycles, due to
the Doppler frequency shift. In using a highly selective
receiver whose final mixer is tuned to receive the
precalculated frequency of an echo return from the moon, the
receiver rejects any signal returned at any other
frequency. To reduce the noise contribution of the
receiver, a high-gain, low-noise-
Propagation studies indicated
that electromagnetic waves at a frequency of
110 mc were capable of penetrating the ionosphere, and because of
availability of equipment, a radar set operating at 111.5 me
was chosen for the experiment. The peak power available
in this transmitter was equivalent to 3000 watts for
Pt
using a 0.25-second pulse. The transmitter had
the added advantage of being crystal controlled,
deriving its final radio frequency after a series of
frequency multiplication from a 516.2-kc crystal oscillator. The
receiver associated with the transmitter was of
the multi-mixer type (quadruple superheterodyne) capable
of beating down radio-frequency signals to a final
intermediate frequency of 180 cycles per second. Such an
arrangement permitted use of an extremely narrow pass
band, 57 cps, thus making the receiver highly selective and limiting
the noise to a very low value. The extremely narrow-band
receiver was an advantage, also, because it permitted tuning the
receiver to the exact radio frequency of the returned
echo. The importance of this can best be realized by
considering the fact that due to the relative velocities of the
earth and the moon, the returned signal may differ from
the transmitted signal by as much as 300 cycles, due to
the Doppler frequency shift. In using a highly selective
receiver whose final mixer is tuned to receive the
precalculated frequency of an echo return from the moon, the
receiver rejects any signal returned at any other
frequency. To reduce the noise contribution of the
receiver, a high-gain, low-noise-
figure pre-amplifier was connected between the antenna and
the receiver proper. The minimum perceptible received
power was P, readily
calculated from the formula for noise figure.
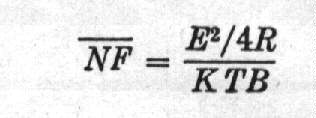 Equation (2)
Equation (2)
In this formula E2/4R
is the maximum available signal power at the receiver
input terminals in watts, where E
is the signal voltage at the antenna terminals, and R
is the effective impedance in ohms. KTB
is the maximum available noise power at the
receiver input, where K
is Boltzman's constant, 1.37 X 10-23
joules per degree Kelvin, T
is the temperature in degrees Kelvin, chosen, at 300
degrees, and B is the
noise bandwidth of the receiver in cycles per second.
For this receiver B
is 57. For a one-to-one ratio Eq. 3
gives signal-power to noise-power of
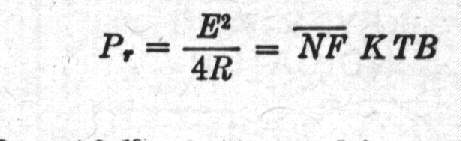 Equation (3)
Equation (3)
1.48 X 10-18
watts, taking the effective noise figure of the receiver as 7
db.
The best antenna available at this frequency was
a 32-dipole array utilized by the SCR-271 early-warning radar.
Two of these arrays were secured side by side and
mounted on a 100-foot tower. Calculations show that
the array had a power gain of 152 times that of a single
halfwave dipole antenna. Since the effective gain
of a single dipole is 1.64 times that of an isotropic
radiator, the value of G.
is given as 1.64 X 152 or 250.
The absorption area A, of the
receiving antenna is calculated from
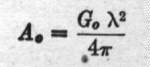 Equation (4)
Equation (4)
Substituting the value of G,
previously given, Ao
= 522.1 X 10-7 square miles. The
remaining constant to be determined before solving Eq. 1 is o
the effective echoing area of the target. Calculations
of the reflectivity coefficient made by Walter McAfee of the
Theoretical Studies Group, assuming zero
conductivity and a dielectric constant of six for the
moon, resulted in the figure 0.1766. The effective echoing
area is this figure multiplied by the projected area of
the moon, Pi d2/4
where d is the lunar
diameter. This gave an effective echoing area of
0.1766 (2160)2 (3.1416)/4 or 647,000
square miles.
Substitution of these values in the free-space
radar equation gave a maximum range of 573,500 miles and
indicated that the effective range of the equipment
chosen was more than twice that needed to receive echoes
from the moon. By adding the power gain due to
ground reflection, a further excess of power of 12 db or a range
of 1,140,000 miles was indicated, which meant that according
to calculations, the received signal should be about
20 db above thermal noise. This calculation of the
signal strength of the returned echo checked closely
with observations and indicated that no appreciable attenuation
occurs in free space.
Transmitter
Once the determination of constant was completed, the
choice of available radar sets was made. Since no
attempt was made to design major components specifically
for this experiment, the selection of receiver and
transmitter was made from equipment on hand. A
crystal-controlled radar transmitter and receiver designed
by Major E. H. Armstrong for another purpose were
selected since they met the requirements of power
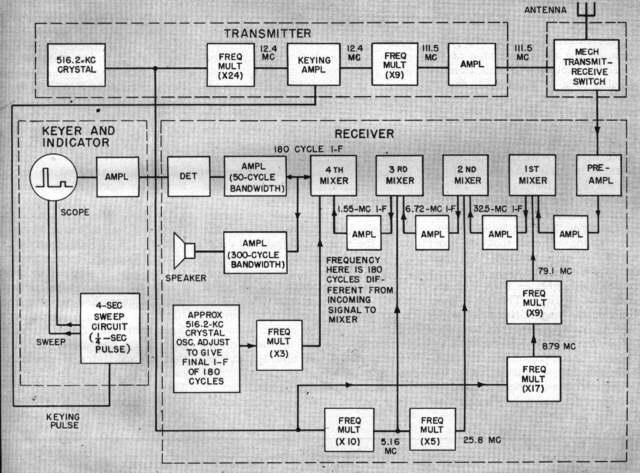
and bandwidth. A block diagram of the complete transmitting,
receiving and indicating system is shown in Fig. 1.
The transmitter is crystal controlled, deriving its final
radio frequency of 111.5 me after a series of frequency'
multiplications from a fundamental crystal oscillator frequency
of 516.2 kc.
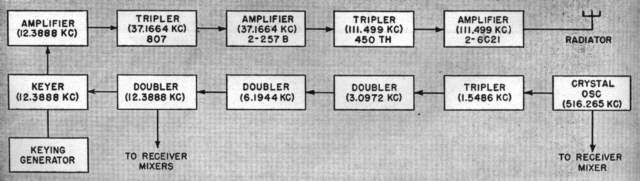
Keying is accomplished by causing a low-level
multiplier stage to conduct by driving its cathode
negative for the duration of the transmitted pulse. In
the initial setup, keying was performed mechanically by a relay,
but this has since been replaced by an electronic keyer
with the pulse width controllable between 0.02
to 0.2 seconds. A block diagram of the transmitter is
shown in Fig. 2.
From the diagram it is apparent that the
transmitter is of a conventional type. The output is fed over
a 250-ohm open-wire transmission line to the antenna
array. The antenna contains 64 dipoles horizontally polarized.
The effective power gain of the array is 250, or 24 db.
The antenna, shown in Fig. 3; is mounted on a steel
tower 100 feet high and is controllable in azimuth only.
No provision has been made to incline the antenna in
elevation. Because of this restriction, the times of
observation using the present equipment were necessarily
limited to moonrise and moonset. That this condition
of observation is the worst possible (due to the long
path through the atmosphere and the consequent
possibility of trapped radiation) has been recognized. But it
was impractical to procure an array of the
equatorial type. Aside from propagation deficiencies, a
far more serious limitation was the fact that observations
were limited to two short periods daily.
 The beam width of the array is
approximately 15 deg at the half-power points, with the
first three lobes spaced approximately 3 deg in
elevation. Since the diameter of the moon subtends
roughly one half degree of arc, most of the power
transmitted does not illuminate the target, which constitutes
a serious waste of power. The rate of rise of the moon
along its ecliptic is 1 degree of are every
The beam width of the array is
approximately 15 deg at the half-power points, with the
first three lobes spaced approximately 3 deg in
elevation. Since the diameter of the moon subtends
roughly one half degree of arc, most of the power
transmitted does not illuminate the target, which constitutes
a serious waste of power. The rate of rise of the moon
along its ecliptic is 1 degree of are every
4 minutes, which allowed roughly 40 minutes of
observation as the moon intercepted the first three
lobes of the antenna. Bending effects due to long
transmission path through the ionosphere undoubtedly
exist, but no precise measurement of this effect has
yet been made.
Receiving System
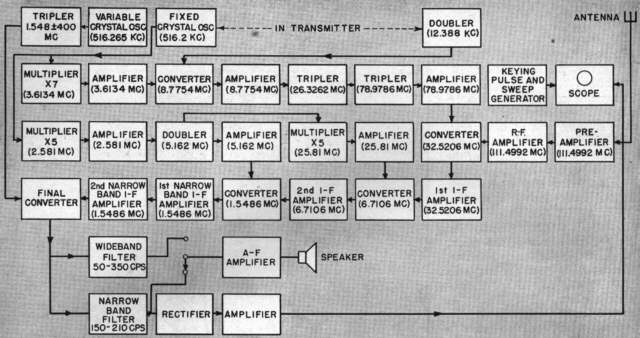
The receiving system is sufficiently different
from conventional design to warrant a more complete
description. A block diagram is shown in Fig. 4. The
entire receiver is frequency controlled, and contains four mixer
stages which heterodyne the radio-frequency signal to a final
intermediate frequency of 180 cps. Since the first three
injection frequency voltages as well as the final radio frequency
are derived from multiples of common crystal oscillator,
a high degree of frequency stability is achieved
in the system. This high degree of stability is
essential to permit tuning the highly selective receiver to the
frequency of the echo signal. This tuning is
accomplished in the final heterodyne stage.
In tuning it is necessary to take account of the
change in frequency of the returned signal which results
from variations in the relative velocity of the moon with
respect to the earth. The frequency of the returning
echo may differ from the transmitted frequency by as much as 300
cycles per second, since the relative velocities of
the earth and moon vary from about +900 mph at moonrise
to -900 mph at moonset. At the frequency of the
transmitter, a relative velocity of 3 miles per hour
between antenna and target causes a shift of approximately
1 cycle per second in the received signal. This
frequency shift, due to relative velocities of the transmitting
antenna and target, is present in all radar echoes from
moving targets, but is undetected in conventional receivers
because the band-width of the normal receiver is many times
greater than the frequency shift. In the Diana receiver,
a band-width of 57 cps is achieved in the final IF
stages. It is therefore necessary to predetermine the Doppler
frequency shift for the particular observation being made, and to
select the proper crystal for the final heterodyne
mixer. To achieve the high degree of accuracy required
in the final mixer, provision is made to modify
the frequency of the crystal-controlled oscillator by means of a
screwdriver control which varies the air gap above
the crystal. Final adjustment of the oscillator is made by beating
the crystal oscillator output against a secondary frequency
standard source, and observing the output on a
monitoring oscilloscope.
The output of the final heterodyne mixer is fed
into two channels, one audio, the other video. The audio
channel is simply a power amplifier stage with the
output connected to a loud speaker. The video output
channel is fed into a second detector to recover the
envelope of the 180 cps intermediate-frequency signal,
and then is amplified by a high-gain video amplifier
and connected directly to the vertical deflecting plates
of a nine-inch cathode-ray tube. The horizontal
deflection is a linear 4-second type-A sweep. The
visible output is the characteristic low-frequency noise
pattern representing a 57-cycle bandwidth centered at
180 cycles. A sudden upward departure from the base
line occurs when an echo signal is received from the
moon. This is shown clearly in Fig. 5. The audible signal
is random noise of 57-cycle bandwidth, superimposed on a
fixed-frequency note, at the intermediate frequency of
180 cycles, when the echo is received.
As stated previously, tuning of the receiver is
accomplished in the final mixer. The injection signal
frequency must be calculated for each observation to
take into account the
relative velocity of target and antenna due to both the
rotational velocity of the earth and the orbital velocity of the
moon. These data, together with azimuth angle and time,
are calculated daily from information given by the
Nautical Almanac and Ephemeris. The detection of the frequency
due to Doppler shift is made with a high degree of
accuracy by the selective receiver. This in itself is
corroboration that the echo signal is from the moon.
Also, the echo interval of 2.4 seconds admits of no other explanation.
The pre-amplifier of the receiver consists of a
three-stage tuned r-f amplifier employing two
grounded-grid stages (654) followed by a 6SH7 tuned
amplifier at the transmitter frequency. The overall gain of
the pre-amplifier alone is 30 db with an overall noise
figure of 3.5 db and a bandwidth of 1 me. The electrical
design of the first two stages was suggested by a
development of Dr. F.B. Llewellyn. A simplified schematic of the
first two stages is shown in Fig. 6. The use of
concentric tubing inductances for the tuned circuits
provides automatic r-f filtering on the direct-current
and filament leads. The pre-amplifier was designed
originally as an improvement kit for the SCR-271 radar, and like
the transmitter and receiver, was chosen for the Diana
experiment because it satisfied one of the requirements, that of
a very low noise figure receiver. A tuned
impedance-matching transformer is used between the
receiver and transmission line to convert the
250-ohm balanced input to the 50-ohm unbalanced input of
the pre-amplifier.
The transmit-receive switching system (t/r box) employed
in the original experiment was a set of two mechanically-operated
shorting bars on the transmission line, operating from
a multivibrator-controlled relay during the transmitted
pulse interval of 0.25 sec. One of the shorting bars
serves to short out the receiver input during transmission,
and the other shorts out the transmitter during
reception.
Keyer and Indicator
The visual indicator used is a nine-inch electrostatic
cathode-ray tube, 9EP7, with a long-persistence screen.
The electron beam is caused to scan the width of the
tube, synchronously with the transmitted pulse, in 4
seconds, forming a linear time base. The persistence of
the tube is long enough to retain the pattern for at
least two sweeps. The circuit employed to generate this sweep
is a direct-coupled transitron sawtooth oscillator,
described below. A pulse equivalent in time to the
keying pulse is also generated by this circuit and is
applied to the cathode of a low-level multiplier stage
of the transmitter, causing it to conduct for the pulse
duration and to drive the subsequent multipliers.
The time-base generator consists essentially of a
high-gain pentode amplifier with capacitance coupling
between plate and grid. The schematic is shown in Fig. 7. The
capacitance coupled path includes a cathode follower
stage, the left hand section of V2
For the duration of the conduction cycle, the anode voltage of
the pentode V1,
drops and capacitor C1,
begins to discharge through the tube. As the voltage on
the plate drops the current flow in C1,
drives the grid negative, tending to cut off the
plate current. A condition of dynamic equilibrium then exists
with the plate voltage dropping at a linear rate
determined by R1,
and C1,
and the grid being maintained at a constant voltage,
since each decrement in plate voltage causes a
corresponding drop on the grid which keeps the grid
signal and hence the output of the tube substantially
constant. The time constant of R1,
C1,
is chosen to cause C1,
to become fully discharged during the cycle.
When the plate voltage drops to the point where
electrons from the cathode can no longer flow to it, an
increase in screen current occurs which rapidly
decreases the screen
voltage and correspondingly decreases the suppressor
voltage. This action, which is cumulative, has the effect
of suddenly cutting off the anode current. This causes
the cathode current to be retarded by the suppressor grid and
made to flow to the screen. A negative pulse appears at
the screen, and C1,
begins to charge through the cathode follower until a
point is reached where the plate begins to draw current
and the oscillator is recycled. The screen returns to
its original voltage, and the plate voltage begins to
fall. By suitable choice of R1,
and C1,
a range of from about 0.1 to 3 cps is obtained.
Keying-voltage signals are derived from the
differentiated output of the negative pulse appearing on
the screen of the oscillator. This is used to
trigger a multivibrator whose time constant is
controllable by a variable 5 meg resistor, varying the
output pulse width from 0.02 to 0.25 seconds.
The addition of the cathode follower stage V2,was
made to shorten the charge time of C1,
by causing it to charge through the grid cathode space
of the cathode follower. This reduces the return trace
time. Tube V3, serves as a
degenerative phase-inverting amplifier to secure push-pull sweep
voltage.
The keyer multivibrator is a conventional cathode-coupled
flip-flop circuit with the initiating trigger applied
as a positive pulse on the grid of the normally
non-conducting section. A positive pulse varying in width
from 0.02 to 0.85 seconds is obtained at the plate of the other
section. This signal is applied to a normally cut off pentode whose load
impedance is the cathode of the 12.388 me amplifier
stage in the transmitter. For the duration of this applied
signal, the plate of the amplifier is driven negative, taking the
cathode of the keying tube down with it, thus
causing it to conduct.
The first echoes from the moon were received at
moonrise on January 10, 1946. The indication was of the
audible type in the form of a 180-cycle beat note
occurring 2.5 seconds after transmission. Although
numerous observations have been made, both at moonrise
and moonset, echo returns do not occur after every
transmission. Further measurements are needed before precise
scientific conclusions can be drawn.
REFERENCE
(1) The Radar Equation, Electronics p. 92, April
1945.




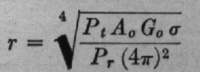 Equation (1)
Equation (1)
 Propagation studies indicated
that electromagnetic waves at a frequency of
110 mc were capable of penetrating the ionosphere, and because of
availability of equipment, a radar set operating at 111.5 me
was chosen for the experiment. The peak power available
in this transmitter was equivalent to 3000 watts for
Pt
using a 0.25-second pulse. The transmitter had
the added advantage of being crystal controlled,
deriving its final radio frequency after a series of
frequency multiplication from a 516.2-kc crystal oscillator. The
receiver associated with the transmitter was of
the multi-mixer type (quadruple superheterodyne) capable
of beating down radio-frequency signals to a final
intermediate frequency of 180 cycles per second. Such an
arrangement permitted use of an extremely narrow pass
band, 57 cps, thus making the receiver highly selective and limiting
the noise to a very low value. The extremely narrow-band
receiver was an advantage, also, because it permitted tuning the
receiver to the exact radio frequency of the returned
echo. The importance of this can best be realized by
considering the fact that due to the relative velocities of the
earth and the moon, the returned signal may differ from
the transmitted signal by as much as 300 cycles, due to
the Doppler frequency shift. In using a highly selective
receiver whose final mixer is tuned to receive the
precalculated frequency of an echo return from the moon, the
receiver rejects any signal returned at any other
frequency. To reduce the noise contribution of the
receiver, a high-gain, low-noise-
Propagation studies indicated
that electromagnetic waves at a frequency of
110 mc were capable of penetrating the ionosphere, and because of
availability of equipment, a radar set operating at 111.5 me
was chosen for the experiment. The peak power available
in this transmitter was equivalent to 3000 watts for
Pt
using a 0.25-second pulse. The transmitter had
the added advantage of being crystal controlled,
deriving its final radio frequency after a series of
frequency multiplication from a 516.2-kc crystal oscillator. The
receiver associated with the transmitter was of
the multi-mixer type (quadruple superheterodyne) capable
of beating down radio-frequency signals to a final
intermediate frequency of 180 cycles per second. Such an
arrangement permitted use of an extremely narrow pass
band, 57 cps, thus making the receiver highly selective and limiting
the noise to a very low value. The extremely narrow-band
receiver was an advantage, also, because it permitted tuning the
receiver to the exact radio frequency of the returned
echo. The importance of this can best be realized by
considering the fact that due to the relative velocities of the
earth and the moon, the returned signal may differ from
the transmitted signal by as much as 300 cycles, due to
the Doppler frequency shift. In using a highly selective
receiver whose final mixer is tuned to receive the
precalculated frequency of an echo return from the moon, the
receiver rejects any signal returned at any other
frequency. To reduce the noise contribution of the
receiver, a high-gain, low-noise-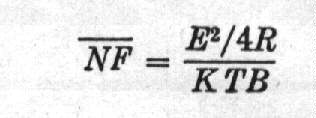 Equation (2)
Equation (2)
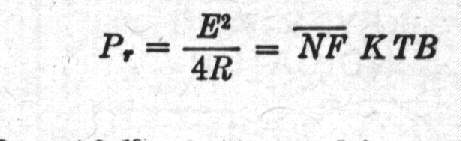 Equation (3)
Equation (3)
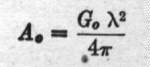 Equation (4)
Equation (4)

 The beam width of the array is
approximately 15 deg at the half-power points, with the
first three lobes spaced approximately 3 deg in
elevation. Since the diameter of the moon subtends
roughly one half degree of arc, most of the power
transmitted does not illuminate the target, which constitutes
a serious waste of power. The rate of rise of the moon
along its ecliptic is 1 degree of are every
The beam width of the array is
approximately 15 deg at the half-power points, with the
first three lobes spaced approximately 3 deg in
elevation. Since the diameter of the moon subtends
roughly one half degree of arc, most of the power
transmitted does not illuminate the target, which constitutes
a serious waste of power. The rate of rise of the moon
along its ecliptic is 1 degree of are every 