DOPPLER PULSE ENERGY
Doppler modulation is a form of frequency modulation, ( FM ) caused by relative motion between the source and detector. Therefore, an FM reciever is required to detect it. The amplitude of ( FM - detected ) Doppler pulses is not as significant or important as the enclosed area of the pulses. ( the "energy" in the pulses ) This is true because the area enclosed by each pulse is directly proportional to the amount of phase shift that occured when the antennas were switched, and ( therefore ) proportional to the cosine of the signal bearing.

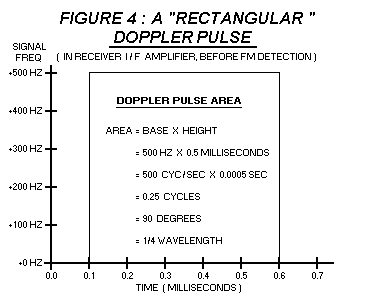
The figure below shows a "rectangular" Doppler pulse, with a deviation amplitude of +500 Hertz, ( in the I/F amplifier, before FM detection ) and a duration of 0.5 milliSeconds. It is possible to calculate the area enclosed in this pulse by multiplying its base ( 0.5 milliSeconds ) by its height. ( 500 Hertz = 500 cycles / second ). This area will be expressed in units of phase shift because cyc/sec x sec = cyc. Note that one cycle = 360 degrees = 1 wavelength.



In this example, the area enclosed by the pulse equals ( 500 cyc / sec ) x ( 0.0005 sec ) = 0.25 cycles, which equals 90 degrees, or 1/4 wavelength. Therefore, the antenna which created this pulse is 1/4 wavelength closer to the signal source than the previous antenna. ( positive pulse polarity indicates it is closer to the source )


DOPPLER PULSE INTEGRATION

FM detectors are, by definition, "frequency to voltage" converters. Their behavior can be characterised with a single specification called the detector co-efficient, expressed in Volts per Hertz. ( input = hertz, output = volts, coefficient = output / input )

By multiplying the Doppler pulse area by the detector coefficient, it is possible to discover how the pulse area will be "expressed", ( what units of measure ) after it is FM - detected. Because the "pre - detection" pulse area is expressed in units of hertz - seconds, and the detector coefficient is expressed in volts / hertz, the "post - detection" pulse area will be expressed in units of ( volts ) x ( seconds), or "volt - seconds". Therefore, it is necessary to feed this ( FM - detected ) signal into a circuit which will translate a signal from "volt - seconds" into volts. If this is done, the resulting voltage will be porportional to the cosine of the signal angle.

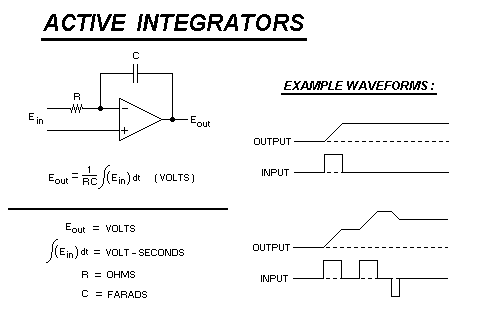
An integrator circuit is suitable for this task. An integrator circuit produces an output voltage which is porportional to the "area" of an input pulse. The term "integration" actually comes from a branch of mathematics called calculus.... It is the name of the procedure that is used to calculate the area underneath a mathematical "curve", plotted on a graph. In electronics, the term "waveform" can be substituted for "curve", so circuits which perform this function are called integrators.

In this D/F, the integration is actually performed by the Switched Capacitor Filter. A close examination of the SCF circuit will reveal that ( in one sense ) it is actually a set of eight RC - type integrator circuits, ( one for each antenna ) which are sequentially selected so that each antenna drives one specific integrator. ( the CD4051 chip is merely a rotary CMOS "switch", with a single pole and 8 switch "positions" )

Just as an FM detector can be characterized with a single specification called the detector co-efficient, so too can an integrator be characterized with a specification called the integration co-efficient. For an integrator, the input signal is expressed in units of volt - seconds, and the output is expressed in volts, so the co-efficient of an integrator would be expressed as volts per volt - second, ( output / input ) or by cancelling the common units, expressed simply as "1/seconds".

Multiplying the ( post - detection ) Doppler pulse area by the integration coefficient will yield the resulting (integrator) output voltage. This voltage (in turn) is porportional to the cosine of the signal direction, as observed by the antenna pair.


ACTIVE INTEGRATORS

Ordinary RC integrators don’t really do a very good job of "integrating" signals... it is probably more accurate to call them voltage "averagers", rather than integrators. They do a reasonable job of integrating a signal if the signal ( 1 ) is periodic or repetitive, ( 2 ) has a fairly low duty cycle, and ( 3 ) the RC time constant is many times greater than the time between successive input pulses. If all these criterion are fulfilled, ( as they are in Doppler D/F’s ) then an RC integrator will do a "reasonable" job of producing an output voltage which is porportional to the area of the applied pulses.... good enough for a Doppler D/F to operate effectively.

An IDEAL integrator ( the MATHEMATICAL definition of an integrator ) is another matter... like elephants, an ideal integrator will never "forget" an input pulse... if a single pulse is applied to the input of an ideal integrator, it will drive the integrator’s output voltage to some non-zero value, ( proportional to the pulse area ) which will remain there INDEFINITELY.... ( assuming no other pulses or signals are applied ) Furthermore, the maximum output voltage of an ideal integrator is not limited to the peak voltage of the applied waveform. ( another drawback of RC integrators )



Ideal integrators don’t really exist, but they can be approximated to a high degree ( at least, for audio signals ) using op-amps. The maximum output voltage is limited only by the supply voltages for the op-amp, and the "memory time" is limited mostly by the leakage rate for the capacitor, and the input impedance of the op-amp.


ACTIVE SCF’S

If a Doppler D/F is constructed with "active" integrators in the SCF, some interesting things should be possible.... In an ordinary SCF, the pulse energy from successive antenna rotations is gradually "lost", ( due to RC leakage ) after 5 RC "time constant" intervals. For an active integrator, this decay rate is radically reduced. More importantly, the output voltage is not limited to the peak voltage of the applied Doppler pulses, so the integrator output can "pump up" to a voltage value which is many times greater than that of the individual Doppler pulses.

Together, these facts imply that the bearing information from any particular ( single ) antenna rotation can be retained and used for a much greater time interval than would be possible from a simple RC integrator SCF. It should therefore be possible to use an antenna array with a greatly reduced radius... possibly even small enough to fit easily onto a PC board. It also impies that Dopplers could be constructed for operation on much lower frequencies... well down into the HF bands, or even lower...

With an active SCF, each antenna rotation adds directly to the total signal of all previous rotations... the signal from the 500th rotation would be just as effective as the signal from the first rotation... In geometric terms, this means that each successive rotation ( electrically ) increases the antenna radius by an amount equal to the actual ( physical ) radius of the array... 100 rotations of an array with a 6 inch diameter would yield as much output signal as one single rotation from an array with a diameter of 600 inches. ( 50 feet )

Any SCF that employs active integrators would require two CMOS switches... one for switching the input signals and one for switching the outputs. Furthermore, some means of deliberately "bleeding" the integrators would be necessary... otherwise, they would endlessly "pump up" until their outputs reached the limits of supply voltage for the op - amps.

Hmmmm..... very interesting.... maybe it’s time for another PC board.....

[HOME PAGE]