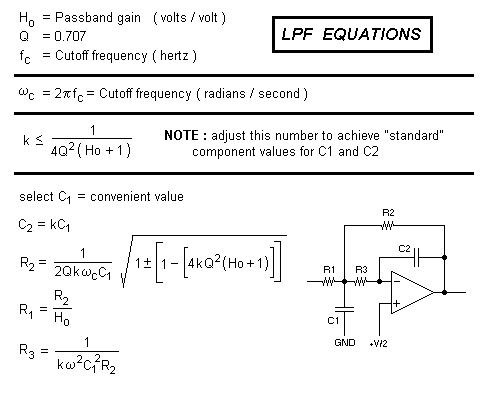
LPF DESIGN EQUATIONS

Note that all the units of measure are WHOLE units...
Ohms for resistance, Hertz for frequency, and FARADS for capacitance. The value of K cannot
EXCEED the quantity on the right side of the equation, but it can be REDUCED, to allow selection
of a "convenient" value for C2.
SCF Design Equations
For such a filter, the low pass cutoff frequency ( -3db ) represents the frequency at which R = Xc. From algebra, it follows that fc = 1/ ( 2pi RC ). For this argument to be valid, the value of C must equal the sum of ALL the capacitors in the filter, because ALL of the capacitors are used for any signal of non-zero frequency. For frequencies other than zero, the actual bandwidth will be doubled, because the filter is capable of responding to signals which lie below the filterís center frequency, as well as those which lie above it.
There is a design trade - off between SCF bandwidth and filter response time... very narrow filters will require more time to "pump up" or "bleed down" whenever the applied signal "changes". ( i.e. the D/F signal direction changes ) Again, intuition can be applied, because the time required for an RC circuit to "stabilize" after a change of input voltage is related to the RC time constant... after one RC time constant "interval", the voltage will achieve 63 percent of itís "ultimate" value, and after 5 RC time constant intervals, the output voltage will reach 99 percent of itís ultimate value. Slow response can actually be an advantage, especially if a digital readout is employed, which would ( otherwise ) suffer from extreme "jitter" in the readout digits.
AN EXPLANATION
The figure below shows the response curves of an simple resonant filter. The amplitude response curve is the familiar "bell" curve that most people know. The phase response curve is probably less familiar, and it represents the the amount of phase shift that occurs to the signal, as it passes throught the filter. Every type of filter exhibits a specific kind of amplitude AND phase response, for various applied frequencies.
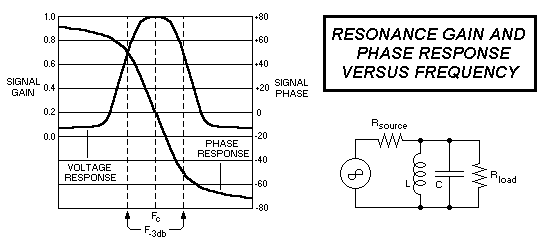
The phase response of a filter is generally not important in the context of ordinary ( voice )
communications circuits, because the human ear is relatively insensitive to phase distortion.... a
violin will still sound like a violin, even if the phase relationship between the various ( audio )
harmonics of a violin are distorted... only the relative amplitudes of the harmonics will
significantly affect the "sound" of a violin.
Resonant filters will have a significant effect on signal phase, unless the driving frequency EXACTLY equals the natural resonant frequency of the filter. In this application, ( Doppler D/Fís ) that causes serious problems, because the phase angle of the signal is important... it is the quantity being measured, to determine signal direction. If a resonant filter ( accidentally ) changes the phase angle of an applied Doppler sine wave, it will also change the indicated signal direction.
CALIBRATION STABILITY
The problem is aggravated by very narrow filter bandwidths... For a resonant bandbass filter, the amount of phase shift introduced by the filter equals 45 degrees at the -3db frequencies, and varies from +45 to -45 degrees within the passband. This means the indicated bearings would also vary 45 degrees ( plus or minus ) from the true value, if the frequency "mismatch" between the clock frequency and the filter center frequency varies by an amount equal to 1 / Q.
For a sharply resonant filter, ( example : Q = 100 ) a frequency mismatch of only 1 percent will throw the D/F calibration off by 45 degrees. This is the dilemma... any resonant filter that would be narrow enough to effectively reject voice audio would also be so sensitive to component changes that it would be almost impossible to maintain D/F calibration.
DOPPLER FILTER METHODS
Low pass filters also exhibit a phase / frequency relationship which will affect D/F calibration, but most of the phase - frequency "sensitivity" occurs near the cutoff - frequency of the filter.... for signals which do not lie near the LPF cutoff frequency, the amount of phase - frequency "sensitivity" is greatly reduced, so it is possible to maintain D/F calibration with simple circuits. For this reason, it is common ( in Doppler D/Fís ) to design the LPFís so that the cutoff frequency clearly lies above the fundamental Doppler frequency, and cleary below the first harmonic.