Quick Summary:  Diode detector insertion power loss can be reduced below the value achieved under impedance matched conditions. The requirements are:  (1) Output load resistance equals twice the RF source resistance.  (2) The Saturation Current and Ideality Factor of the diode are such that the very-low-signal output resistance of the detector equals the output load.

It is usually assumed that power loss in a two port device (here, a crystal set) is minimized when its input and output ports are impedance matched.  This article will show that this is not true in the case of a diode detector operating at a signal power level well below that of its region of essentially linear operation.  In the linear region audio output power is proportional to RF input power.  That is, for every dB of change in input power there will be one dB change of output power.  In the lower power region, called the 'square law' region, a change of one dB in input power results in a two dB change in output power.
 

Definition of terms:

Rd:             Resistance of a diode at its axis crossing. Rd=0.0257*n/Is at 25 degrees Celsius
Ri:              RF input resistance of the detector
Ro:             Output resistance of the detector
R1:             RF source resistance looking toward the tank
R2:             Output load resistor
Is:               Diode Saturation Current
n:                Diode ideality factor
T:                Parallel LC tuned circuit
LSC point:  The operational point half way between linear and square law operation
Plsc(i)         Max. available input power at the linear-square-law crossover point 

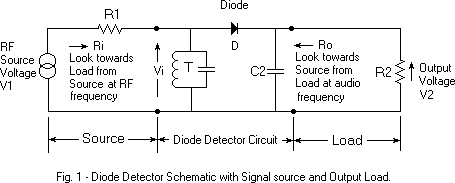
It has been asserted in previous Articles that the RF input and audio output resistances, Ri and Ro, of a diode detector approach the same value and equal 0.0257*n/Is = Rd ohms at room temperature when the input signal strength is low enough.  See Article #0, part 3, Article #4, part 2 and Article 16 for information on Is and n, and ways of measuring them.

Fig. 1 represents a conventional diode detector.  The tank circuit T is shown with no internal loss.  A real world tank will have loss that can be represented by a shunt resistor connected across it.  For convenience of analysis it is assumed that this loss resistance is absorbed into the source V1, R1  (For a more complete explanation, see Article #1, first paragraph after the third schematic.).  Impedance transform the source (antenna) and load (headset) resistances to equal values (R1 = R2) and select a diode that has an Rd equal to them.  This will result in a reasonable impedance match at both the input and output if the signal power level places operation below +10 dB of the linear-to-square law crossover point.  Little input power directed towards the detector will be reflected back to the source and most all of the output power from the detector will be absorbed in the load, R2.  If the diode detector were a linear device with linear input and output resistances, this impedance-matched condition would result in the least detector power loss (greatest sensitivity) obtainable.  It would seem clear that the crystal set detector cannot be made more sensitive.  Actually, not so!  Very weak signal sensitivity can be improved, theoretically, by about 2 dB while using the same power source (V1 and R1).  This gives a hard-to-hear increase in volume, but every little bit helps.

In the impedance matched condition discussed so far, R1=Ri=Rd and R2= Ro.  Simple math shows that the detector input voltage Vi will equal one half the internal source voltage V1.  If we create an impedance mismatch between the source resistance R1 and the detector input resistance Ri by replacing the diode D with a different one having one-half the saturation current, Vi will increase.  The reason is that the detector input resistance Ri is now twice R1 and the voltage divider made up of R1 and Ri will reduce V1 by only one third at the input of the diode..  A higher input voltage to the diode should result in a higher output power to the load R2.  Since the new diode will have double the output resistance than the old one, all of the benefit from the greater value of Vi could be lost by the greater voltage division between the (now two times higher) detector output resistance and the load R2.  All is not lost, however, since the detector is operating in the square law (weak signal) region.  Even though the two voltage division actions tend to cancel (for small changes), the detector output will be higher because of square law operation. 
 

Fig. 2

Fig. 3

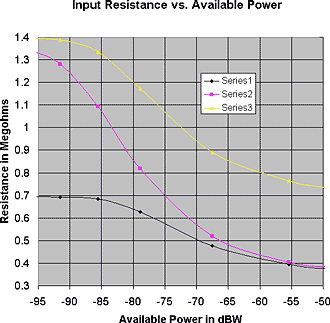
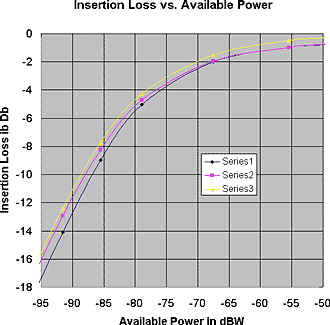
Theoretical calculation and Spice simulation show that that in a crystal set having equal values for R1 and R2, the diode parameters that give to lowest insertion power loss at low signal power levels fit the equation: R1=R2=2*(0.0257*n/Is)=Rd at room temperature.

Now let us look at the effect on Ri and insertion power loss if Ri does not match R1.  Look at Fig. 2.

1. Series 1: The diode has an Is of 38 nA and an n of 1.03.  R1= R2=Rd  The graph shows that Ri is 700k ohms at low input power levels and that it decreases towards 350k ohms at high input levels, where the detector acts as a peak detector.  Not graphed, Ro, changes from about 700k to 1400k ohms as the input power goes from -95 dBW to -50 dBW.  It is 1190k ohms at the LSC input power point of -78.9 dBW.   See part 4 of Article #0.
2. Series 2: The Is of the diode is changed to 19 nA.  All else stays the same.  Ri approaches 1400k ohms at low input power levels and decreases towards 350k ohms at high levels.  Not graphed, Ro is approximately 1400k ohms at low input power levels and 1400k ohms at high output levels.
3. Series 3:  The diode Is stays at 19 nA,  the n at 1.03, R1 at 700k ohms and R2 changes to 1400k ohms.  Ri changes from about 1400k to 700k ohms when going from low to high power levels.  Not graphed, Ro is approximately 1400k ohms at low input power levels and 1400k ohms at high levels.

What does all this mean?

• Compared with the impedance matched condition, an increase in the volume of weak stations can be achieved if the source resistance is dropped to 1/2 the input resistance of the detector, leaving the output matching unchanged.  Looking at it in a practical way, the RF source impedance may be fixed.  That means, compared to the impedance matched condition, the Is of the diode should be halved and the output load resistance doubled.  Put another way, the output load resistance should be twice the RF source resistance, and equal to the axis-crossing resistance, Rd, of the diode.
• This higher value for the audio load resistance may be created by changing the impedance transformation in an audio transformer.  Be warned that the insertion power loss of an audio transformer tends to increase when one operates it at higher input and output resistances than it was designed for. It is possible for increased transformer loss to cancel out some of the 1.9 dB improvement.  See Article #5 for info on the loss in various audio transformers.
• Many diligent experimenters probably have already converged their crystal set designs to include this info. 

 Return to Home Page