A Procedure for Measuring the Sensitivity (Insertion
Power Loss), Selectivity and Input/Output
Impedance of a Crystal Radio Set.
By Ben H. Tongue
Quick Summary: This Article
describes a device and procedure for quantifying several characteristics
of crystal sets. They are: (1) Insertion power loss, (2) Selectivity,
(3) RF input impedance match and (4) Audio output resistance.
First, an acknowledgement: This article was inspired by a paper
written on 9/15/99 by Charlie Lauter at: Lautron@aol.com . It can
be accessed at: http://home.t-online.de/home/gollum/testing.htm .
He led the way with a good procedure for sensitivity and selectivity measurement,
but I wanted a more general approach. Here is mine:
Definitions and Acronyms used in this Article
| abs |
Absolute value (sets the next expression to a positive value). |
| AMCS |
Apparatus for use when Measuring Crystal Set Insertion Power Loss and
Selectivity. |
| CSUT |
Crystal Set under Test. |
| D |
Difference between RF envelope peak-to-peak and valley-to-valley voltage. |
| DUT |
Device Under Test. |
| Eo_pp |
Peak to peak demodulated output voltage |
| FLVORA |
Fixed Loss, Variable Output Resistance, Attenuator. |
| ILCS |
Ideal Lossless Crystal Set. |
| IM |
Impedance Match. |
| IPL |
Insertion Power Loss in dB. |
| Is |
Saturation Current of a diode. See Article #1 for an explanation
of this term. |
| MAP |
Maximum Available Power, in Watts. |
| MASP |
Maximum Available Sideband Power, in Watts. |
| n |
Ideality factor of a diode. See Article #1 for an explanation
of this term. |
| p-p |
Peak to peak. |
| Po |
Detector Output Power, in Watts. |
| sqrt |
Square root of the expression that follows. |
| RL |
Detector load resistor. |
| Ro |
Detector Internal Output Resistance. |
| S-3 |
Frequency difference between two points 3 dB down on the selectivity
curve. |
| S_20 |
Frequency difference between two points 20 dB down on the selectivity
curve. |
| S11 |
Voltage Reflection Coefficient. |
| Suffix |
See the paragraph above Fig. 3 for the suffix labelling conventions
used when measuring IPL. |
| SF |
Shape factor, the ratio of the 20 dB down bandwidth to the 3 dB down
bandwidth. |
| SG |
Signal Generator. |
| SPHP |
Sound Powered Headphones. |
| SPICE |
A computer program used to simulate the physical operation of circuits. |
| Vs |
RF Voltage source |
| VSWR |
Voltage Standing Wave Ratio. |
This article is divided into six sections. The first describes the IPL
(Insertion Power Loss) measurement method. The second gives a theoretical
derivation. The third shows a method for the measurement of selectivity.
The fourth shows how to measure the input impedance match of a CSUT (Crystal
Set Under Test). The fifth shows a method for measuring the output
resistance of a Crystal Set. The sixth gives some comments and suggestions
on how to improve crystal set performance.
A quick definition: The IPL of a crystal set may be loosely defined
as 10 times the log of the ratio of the audio power delivered to
the output load divided by the maximum RF sideband power available
from the antenna.
Here comes a more rigorous definition of IPL: The function
of a crystal set is to convert (demodulate) the modulated RF signal sideband
power received by the antenna-ground system and deliver as much of that
power as possible to the output load as audio output power. Understand
that all of the signal information modulated on a carrier and picked up
by an antenna-ground system resides in the power carried in the sidebands
of that signal. No signal information is contained in the RF carrier.
The Insertion Loss Method assumes that a voltage source with a specific
internal impedance is connected through a “device under test” (DUT) to
a load resistor. We can say that the DUT is “inserted” between the
source and the load.
-
First, consider what happens when an Ideal Lossless Crystal Set (ILCS)
is inserted as the DUT, tuned to the source signal and adjusted for maximum
output. It is connected between the signal source and a Load Resistor
(Rl) representing the average impedance of the headphones to be used later.
This ILCS presents a perfect impedance match to the signal source and also
to the output load. It has no internal power losses. The ILCS
will convert all of the Maximum Available Sideband Power (MASP) in
the modulated signal source into useful audio power in the output load.
Power loss is zero when the ILCS is inserted as the DUT.
-
Second, consider what happens when a real world Crystal Set is inserted
as the DUT. It probably will not present a perfect impedance match
to the signal source nor perfectly match the output audio load, thus incurring
mismatch losses. It will have some internal power losses. Its
output audio power will be less than that of the ILCS. The IPL
of the CSUT is: IPL = 10*log ((Output power of CSUT)/(Output power
of ILCS)) dB.
Now, a brief detour to explain the concept of MAP (Maximum Available
Power) and a more detailed look at Insertion Power Loss (IPL) as used in
this Article.
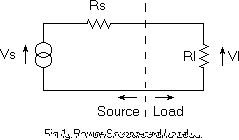
Maximum Available Power (MAP)
Assume that any electrical source of power can be represented as a
voltage source (Vs) that has an inaccessible internal impedance Zs = Rs
+ jXs. See Fig. 1. Assume that the reactance component (Xs)
of this impedance is tuned out. The crystal set tuner should do this
by generating a series reactance whose value is the negative of Xs.
There is a maximum amount of power that Vs, with its internal series resistance
Rs, can deliver to any load. The value of the load (Rl) for maximum
power transfer is Rs itself. This is called an impedance matched
condition. Any other value for Rl will absorb less power from the
source than a value of Rs.
Here is how to calculate MAP from the Vs and Rs combination. As
mentioned before, the maximum power output occurs if Rl = Rs. This
means that the total load on Vs is the series combination Rs + Rl = 2*Rs.
Since power in a resistor can be calculated as (V^2)/R, the total power
dissipated in the two resistors is (Vs^2)/(2*Rs). Since one half
of the power is dissipated in Rs (and lost) and one half in Rl, the maximum
power deliverable to Rl is: (Vs^2)/(2*Rs)/2 = (Vs^2)/(4*Rs). We will
use this relationship later on. Note that Vs^2 means Vs squared and
4*Rs means 4 times Rs. Vs is in RMS volts. If Vs is given
in peak or peak-to-peak units, a correction factor must be applied.
Definition of IPL when the input signal is an RF carrier, modulated
by a sine wave.
Input Power: Audio information that is amplitude
modulated on an RF carrier is contained solely in what are called sidebands.
Sidebands are better called side frequencies if the audio modulation waveform
is a single sine wave, as will be the case here. In sine wave AM,
two side frequencies are generated in the modulator. One is at a
frequency above the carrier and one is below it. They are each spaced
away from the carrier by an amount equal to the modulation frequency.
These two side frequencies carry all the information that is in the signal.
The RF carrier carries none. When we receive a signal on our crystal
set it is this sideband
power that we want of capture and convert
to audio power in our headphones. The carrier acts only as
a “carrier” for the sidebands and generates the DC diode current and DC
voltage across the DC resistance component of the load.
Output power and IPL: Assume that an RF source with a MASP
of Pa Watts is connected to a CSUT and that the CSUT feeds a load resistor.
The source has an internal RF impedance of Za Ohms and the load has an
impedance of Rl. The SCUT is tuned and adjusted to deliver maximum
audio power to the load, with the desired selectivity. Define the
output power as Po. Now imagine the replacement of the CSUT with
an ILCS. It provides a perfect impedance match to the source and
perfectly matches the load. Its output power will equal Pa because
there are no losses. This ideal crystal set will function as a device
to convert all of the MASP into audio power. The ratio of
the output power of the CSUT to that of the ICS set is Po/Pa. This
ratio, expressed in dB is the IPL of the CSUT. IPL = 10*log (Po/Pa)
dB. The load resistor should have a value equal to the average impedance
of the headphones to be later used with the CSUT. (See Article #2 on how
to measure headphone impedance.)
Section 1. IPL Measurement Method.
The test equipment required is:
-
An RF signal generator (SG) covering 530 -1700 kHz and capable of linear
amplitude modulation up to 50%. The generator can be a modern function
generator or a conventional RF signal generator, provided that the RF waveform
has a reasonably low harmonic content. It should have a 50 Ohm output
resistance.
-
A scope with a flat response to at least 1.7 MHz and an accurate calibrated
vertical sensitivity of 0.002 V per division or better. Input resistance
is assumed to be 1 Megohm. Input capacitance (including that of the
connection cable) is assumed to be about 175 pF.
-
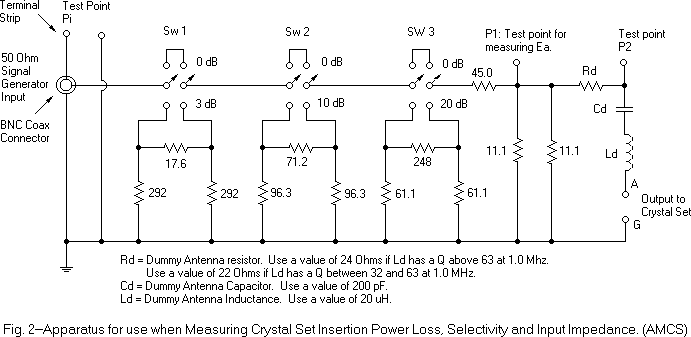
A special attenuator set up and impedance adjuster unit called AMCS.
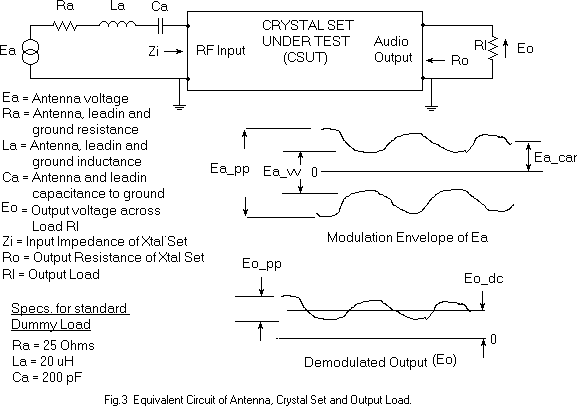
The signal source is modelled as a voltage source Ea with series internal
impedance elements of Ra, La and Ca. See Fig. 3 The components
Ra, La and Ca are intended to have the same impedance as the average antenna
that used to be used for AM reception in the USA. These components
are termed a “dummy antenna” and are specified for use in standardized
testing of AM receivers. The standard is described in “Standards
on Radio Receivers”, Institute of Radio Engineers (predecessor of the IEEE),
New York, 1938.
It is assumed that by tuning the CSUT for maximum output volume, that
the best conjugate impedance match possible is presented to the antenna.
In simpler terms, tuning for maximum volume adjusts the resistance component
of Zi to as close to 25 Ohms as possible and the reactive component of
Zi to as close a value as possible to the negative of the reactance of
La and Ca in series. This set of circumstances transfers the most
signal power possible from the antenna to the CSUT.
The test procedure that follows involves applying a modulated
RF Voltage (Ea) through a dummy antenna to the input of the CSUT and then
measuring the Audio Output Power (Po) delivered to the output load.
The IPL of the CSUT is calculated as: IPL = 10*log (Po/(MAP in the sidebands
of Ea)).
Measurement of IPL
We will use use a special attenuator box between the SG and the CSUT
and call it the AMCS. Refer to the schematic in Fig. 2. The
AMCS has one 3 dB and one 20 dB attenuator that are used in measuring selectivity.
It has an additional 10 dB attenuator in the event some extra attenuation
is needed. The 20 dB attenuator can also be used to determine the
voltage Ea at test point P1 when it is so low that it is hard to read.
The series 45.0 and two parallel 11.1 Ohm resistors form a “minimum-loss
impedance transforming attenuator”. Its input design resistance is
50 Ohms. Its attenuation is set so that the ratio of the voltage
at test point Pi to that at P1 is 10:1. The source resistance feeding
the Dummy Antenna and Crystal Set series combination is 5.25 Ohms.
Two 11.1 Ohm resistors are used in place of one of 5.55 Ohm resistor because
resistors under 10 Ohms may be hard to find. Also lead inductance
is minimized. If the 45.0 and 11.1 Ohm resistors are held to within
+/- 4%, the attenuation accuracy will be within +/- 0.33 dB. of nominal.
Resistor accuracy tolerances for the other attenuators, to hold a +/- 0.33
dB accuracy are: 3 dB-10%, 10 dB-4% and 20 dB- 2.5%.
The load on the CSUT must be a resistor (R1) of value equal to the average
impedance of the headphones used with the crystal set. One can determine
the impedance of the headphones by building and using the FLVORA described
in Article # 2 of this series. Alternatively, it may be estimated
as 5 or 6 times the DC resistance of the phones.
To measure the IPL of a crystal set, connect the SG**** to the AMCS
and set it to a test frequency of, say, 1.0 MHz. Turn on the sine
wave modulation function and adjust the frequency to 1000 Hz**** and the
modulation percentage to 50%****. (50% modulation exists when Ea_pp
is three times Ea_vv.) Connect the AMCS to the antenna and ground
terminals of the CSUT. Connect the scope to Rl and set it to a sensitivity
of 2 mV/div. Set the SG to a high RF output and tune the CSUT to
maximize the 1000 Hz trace on the scope****. Reduce the SG output
as necessary to keep the scope trace on scale****. Reset the SG to
deliver a 4 mV p-p trace on the scope. Connect the scope to point
P1 and measure and record Ea_pp and Ea_vv at Point P1.
| **** |
-
Some RF signal generators have too much harmonic waveform distortion in
their output to give accurate results with this procedure and will need
a simple harmonic filter to clean up the output. If the RF waveform
looks like a fairly good sine wave it's OK.
-
1000 Hz is chosen instead of the usually specified 400 Hz because most
high performance crystal sets use an audio transformer to drive the headphones.
At 400 Hz, the impedance of most transformers is well below the average
value between 300 and 3,300 Hz. Also, transformer loss and distortion
is usually greater at 400 Hz than at 1000 Hz.
-
The usually specified modulation percentage is 30 %. I suggest using
50 %. This gives a greater output voltage and makes low signal level
measurements easier.
-
This test procedure uses one scope at several input attenuator settings
as well as at 1000 Hz and 1.0 kHz. It depends upon calibration accuracy
from one switch position to another as well as from 1.0 kHz to 1.0 Mhz.
I got caught on this. My scope is 21 yeas old and the frequency response
flattening trimmers in the vertical attenuator had drifted. This
didn't affect the accuracy at low frequencies, but produced error at 1.0
Mhz. The best way to check for this problem is to use a quality,
fast rise-time Square Wave Generator and check for a good clean corner
at the leading edge of a 100 kHz square wave. Another option is to
use a sine wave Function Generator, the output of which is known to be
flat vs. frequency. If it has an output up to over 10 Mhz, the output
is probably flat from 1.0 kHz through 1.0 Mhz.
-
One probably will find an undue amount of noise, hash and carrier RF on
the scope screen when measuring the output waveform. This can be
caused by capacity coupling in the transformer between the hot end of the
primary winding and the hot end of the secondary. I eliminate this
hash by using a very simple low-pass filter. To do this, connect
a 100k Ohm resistor in series with the scope input cable, very close to
where it connects to the transformer output terminal. Assume that
the scope has a one Megohm (check it!) input resistance, in parallel with
a 175 pF input capacity when using the probe at the X1 setting. (These
are the values for my Tektronix model T922 scope.) At 1000 Hz the
voltage divider from the series 100k Ohm resistor and the input impedance
of the probe causes the scope to read 0.87 dB less than the actual output
of the CSUT. At 1.0 MHz the attenuation will be will be 41 dB.
Keep the leads short to minimize 60 Hz hum pick-up. Only use the
100k resistor when measuring the output at 1000 Hz. Don't use it
when measuring RF at the input. When calculating IPL, correct your
results for the 0.87 dB loss (Use 0.9 dB).
-
The output sine wave may look distorted. This can come from modulation
distortion in the signal generator or distortion generated in the CSUT.
Generator distortion is not very important here. Distortion generated
in the CSUT can be caused by an incorrect resistance in the parallel RC
used in series with the audio transformer primary (if one is used).
To check, replace the resistor with a pot and adjust it for minimum distortion.
BTW, this is the best way to find the correct value for the resistor.
See Article #1 of this series.
|
Here are the labelling conventions that will be used. Voltages
on the input side of the CSUT always start with Ea.
Voltages on the output side start with Eo. The underscore
is a separator from the description suffix that follows. fo
= carrier frequency, fmod = modulation frequency, pp
= peak-to-peak, vv = valley-to-valley, car =
carrier,
dc = direct current, sf = side-frequency,
carpp
= carrier peak-to-peak, 1sfpp = one side-frequency peak-to-peak,
1sf
= one side-frequency, 2sf = two side-frequencies.
The IPL of any crystal set depends upon the output power level at which
it is operating. At very low output levels (signal barely readable
with sensitive headphones), the IPL increases about 6 dB for every
6 dB reduction in input power. This results in a 12 dB reduction
in output power. When this happens, the diode detector is said to
be operating in its “square law region”. Because of this effect,
I suggest that the IPL be measured at several audio output power levels
when characterizing a crystal set, maybe -80 and –110 dBw.
Section 2. Derivation of IPL.
Figure 3 shows of the envelope of an AM carrier of frequency fo, modulated
at 50% by a sine wave of frequency fmod. This modulation produces
two side frequencies separated from the carrier by fmod. One is above
fo and one is below it. If no side frequencies were present, Ea_pp
would equal Ea_vv and the modulation envelope would be straight lines.
With some modulation is present, one half of the total envelope fluctuation
is caused by one side-frequency and one half by the other. Two side frequencies,
each of amplitude Ea_sfpp, when added to a carrier of amplitude Ea_carpp,
will cause the modulation envelope to have a maximum value of Ea_pp = Ea_carpp+2*(Ea_1sfpp).
The minimum value of the envelope will be Ea_vv = Ea_carpp-(2*(Ea_1sfpp)).
Define:
D
= (Ea_pp)–(Ea_vv) = 4*(Ea_1sfpp). Rearranging terms, we get:
Ea_1sfpp = D/4. We can calculate the MAP of one side-frequency as:
MAP_1sf = ((Ea_1sfpp/(2*sqrt2))^2)/(4*Ra). The first “2” changes
the value of Ea_1sfpp to a peak value. The “sqrt2” changes the resultant
peak value to RMS. The equation, restated, is MAP_1sf = ((Ea_1sfpp)^2)
/ (32* Ra). The total power in the two side frequencies is twice
that in one side-frequency and is: MAP_2sf = ((Ea_ 1sfpp)^2)/(16*Ra).
Now, substituting Ea_1sfpp = D/4, we get: MAP_2sf = (D^2)/(256*Ra).
The output waveform shown in Fig.3 is a sine wave Eo_pp, having a DC
value of Eo_dc. The audio power it supplies to the output load Rl
is: Po = ((Eo_pp/(2*sqrt2))^2)/Rl. The “2” and the “sqrt2” are needed
as before to change Eo_pp from a peak to peak to an RMS value. Simplifying,
Po = ((Eo_pp)^2)/8*Rl. Since IPL = 10*log (Po/MAP_2sf), we can state
the Final Result we've all been waiting for, and it is:
INSERTION POWER LOSS = IPL = 10*log (32*((Eo_pp/(D))^2)*Ra/Rl).
The MAP of the RF carrier only from the AMCS to the CSUT is:
((Ea_pp + Ea_vv)^2)/(3200) Watts.
Section 3. Measurement of Selectivity:
Here is a method for measuring selectivity using the instrumentation
used for measuring IPL. It is adapted from Terman’s “Radio Engineer’s
Handbook: Measure the frequency difference between two points that
lie 3 dB down on the selectivity curve. I’ll call this value S_3.
Measure the frequency difference between two points that lie 20 dB down.
I’ll call this S_20. The input is measured at test point P1. Depending
upon the input signal level chosen for this measurement, the detector may
not be operated in the linear part of its operating region, but partly
into its square law region. This non linearity will cause an erroneous
result if the measurements are made using a constant input signal level
and then measuring the output at each of the four frequencies. The
correct method is to measure the input required at test point P1 to attain
the specified fixed output level at each of the four frequencies.
The non linearity will now be the same for all measurements and cancel
out. The Shape Factor (SF), of the selectivity curve of a CSUT, at
a particular RF frequency and output audio power is defined as SF = ((S_20)/(S_3)).
The lower the number, the better.
Things to remember: The selectivity of a CSUT varies, depending
on coupling, tap settings and frequency of measurement. It is suggested
that measurements be taken at 550, 1000 and 1650 kHz and any other ones
where you think there might be a large variation from the average.
With fixed coupling settings, the SF of a CSUT can change if the input
signal power is changed. This effect can be minimized if the correct
an audio transformer is used with a correct parallel RC in series with
the cold lead of the primary of the transformer. See Article #1.
Section 4. Measurement of Input Impedance Match
Impedance Match (IM) refers to how closely the input impedance of a
device equals the conjugate of the impedance of the source driving it.
We will define the IM of a CSUT only at the frequency to which it is tuned.
It's assumed that the input impedance is resistive at this frequency.
Impedance match may be defined in terms of "Voltage Reflection Coefficient"
(S11) or Voltage Standing Wave Ratio (VSWR). Either can be calculated
from the voltages appearing at test points P1 and P2. Turn off the
modulation of the SG. Define: RF voltage at P1=EP1_pp and voltage
at P2 = EP2_pp. S11 = 20*log abs(1 - 2*(EP2_pp/EP1_pp)).
VSWR = (1 + abs(1 - 2*(EP2_pp)/(EP1_pp)))/(1 - abs(1 - 2*(EP2_pp)/(EP1_pp)))
These calculations define how closely the input impedance of the crystal
set matches that of the IEEE standard dummy antenna.
Section 5. Measurement of the Output Resistance (Ro) of
a Diode Detector.
The addition of a variable resistor and an ohmmeter are needed to measure
the output resistance of the CSUT. Connect the SG, AMCS and scope
as before. Set the fo of the SG to 1 MHz and the AM modultaion to
about 50% at 1 kHz. Connect the variable resistor to the output of
the CSUT and set it to the nominal audio load resistance for which the
SCUT is designed. Call this value RL. Pick a moderate input
power, say one that delivers an audio output power (Po) of -75 dBW to RL.
An output power of -75 dBW is indicated when the 1 kHz p-p output voltage
Eo_pp is: sqrt(RL*(31.6*(10^-9))). Increase the load resistor
to a value 1.3*RL and call the resulting demodulated output voltage Eohi_pp.
Reduce the resistor to 0.7*RL and call the new output voltage Eolo_pp.
Ro = 1.3*RL*((Eohi_pp - Eolo_pp)/((13/7)*Eolo_pp - Eohi_pp)).
Ro varies with change of input power. At low input power levels,
Ro, measured at the diode detector output (before any step-down from an
audio transformer), will equal about 0.026*n/Is. At high input power
levels, in the region of peak detection, Ro will approach twice the antenna-loaded
RF tank resistance.
Section 6. Comments.
-
Remember that output transformer loss is included in the measurement of
IPL. The usual audio transformer loss is in the range of 0.5-2 dB,
but some are higher. It's a good idea to to check the loss of the
one being used. A method is given in Article #5. Don't forget
to reduce the calculated IPL by the 0.9 correction factor if you are using
the 100k resistor in series with the scope. The MAP of the RF
carrier only from the AMCS to the CSUT is: ((Ea_pp + Ea_vv)^2)/(3200)
Watts.
-
It's possible for two different CSUT to have the same IPL at moderate input
signal powers, but differ when receiving weak stations or strong ones.
Very
low input signal performance is enhanced (better DX) if the
RF tank resonant resistance and transformed audio load can be made a high
value. This enables the optimum diode to be one of a lower Saturation
Current. The result is less IPL at low signal levels. See Article
#1. Very high input signal performance is enhanced (louder
maximum volume) if diode reverse leakage is kept low. This point
is often overlooked. Diodes vary greatly in reverse conduction current.
There are two kinds of reverse current effects: One is a gradually
increasing reverse leakage current that loads the circuits more and more
if the input signal increases, maybe by tuning to a stronger station.
It acts as sort of an automatic volume control and is rather rare.
Unfortunately, this effect reduces the maximum volume one can get from
the crystal set. The other is normal reverse current that
increases rapidly above a certain input signal power and causes audio distortion
as well as reduced volume. This effect can be observed when performing
the IPL tests. For instance, in my single tuned loop set, several
Agilent 5082-2835 in parallel, while very good with low signals, distort
when the input carrier power at 50 % modulation gets above about -35 dBW.
Several Agilent 5082-2800 or HSMS-2800 work fairly well at low signal levels
but do not distort at the highest signal level I can supply. This
improvement comes about because the HSMS-2800 has much less back leakage
current than does the HSMS-2820 or 5082-2835 at high reverse voltages.
This effect is more noticeable if the diode load resistance is above the
optimum value than if below it.
-
If you use an audio transformer, don't forget to replace the R in the parallel
RC with a pot and adjust it for the least audio distortion. Actually, I
keep a pot in there all the time because the optimum value is usually zero
for weak signals and about 1/2 the loaded RF source resistance driving
the diode for strong signals.
-
For a given amount of output audio power, the output voltage is proportional
to the square root of the output load resistance. This may cause
a problem for those who use 300 Ohm Sound Powered Headphones (SPHP) and
those who may want to make measurements at low output power levels.
With the suggested starting output of 0.002 V p-p, the output power to
a 1200 Ohm load (SPHP elements in series) is -94 dBW. It would be
-88 dBW @ 0.002 V p-p if the SPHP elements were wired in parallel.
-
To take readings at a lower power level, there are several options to consider:
-
Use a more sensitive scope.
-
Use a low noise 10X gain audio amplifier. An an improvement on this
would be a single tuned band-pass amplifier tuned to 1,000 Hz. It
will filter out some of the noise and hum that will probably be present.
-
Temporarily, for the tests, use an output audio transformer that transforms
to a higher output resistance, along with its corresponding load resistor.
Going from a 300 Ohm to a 12,000 Ohm output resistance will boost the output
voltage by sqrt (12,000/3,00) = 6.3 times. I use two A.E.S. P-T157
transformers connected as shown in the first schematic in Article #5 as
a variable-impedance-ratio transformer to boost the audio signal voltage.
I also use it to experimentally determine if the load on the diode equals
the output resistance of the diode. The switch position that gives
the most output voltage is the one that provides the best match: (4, 16,
63 times ratio, or near the mean of two of the adjacent values).
-
Here are some test results with my single tuned crystal set that uses a
14 " square loop wound with #12 ga. solid wire for the resonator.
The average parallel shunt loss resistance of the tank is 700k Ohms over
the frequency range of 550-1650 kHz.. I use three Agilent 5082-2835
diodes (Is = 38 nA) in parallel for the detector and an audio transformer
to convert the 700k Ohm (low signal) AC output resistance of the diode
detector down to a 12,000 Ohm load resistor. I have not yet set up
to measure a loop set directly, but have coupled in an external antenna
connection to a tap on the tank 6 turns from ground. This, of course,
loads the tank and results in a lower tank resistance than 700k Ohms.
The input impedance match is very good The measured IPL at 1.0 MHz
using the external antenna-ground connection is 9.65 dB at an input carrier
power of -84 dBW, giving an audio output power of -102.9 dBW.
The noise and hash on the scope prevented the measurement of selectivity.
Measurements were then made at a carrier input power of -69.4 dBW.
The output audio power became -82.9 dBW, IPL = 4.5 dB, -3 dB
RF bandwidth = 30 kHz and SF = 9.0. Tapping the antenna 2 turns from
ground increased the -3 dB selectivity to 8 kHz, kept the SF at 9.0 and
increased the IPL by about 4.9 dB. Note: The IPL figures use the
0.9 dB correction for the 100k resistor feeding the scope cable and also
include the estimated transformer loss of 0.4 dB. A SPICE simulation
of this set-up with no loss in the tank gives, for the 6-turns-from-ground
tap condition, an IPL of of 6.1 + 0.4 (for the output transformer) = 6.5
dB instead of the 9.6 dB and 1.7 + 0.4 (for the transformer) = 2.1 dB instead
of the 4.4 dB. This suggests a tank loss of about 2.7 dB.
-
The lower the IPL crystal set, the more noticeable will some of the effects
noted above become.. The use of a parallel RC in the transformer
primary for reducing distortion when receiving strong signals is important
if the audio load resistance is higher than the output resistance of the
CSUT. If the audio load resistance is lower than the output resistance
of the SCUT, it becomes less important. This effect shows up in simple
Xtal Sets that do not use an audio transformer. Here, the headphone
impedance is usually lower than the output resistance of the Xtal Set.
Also, the headphones' DC resistance, as a fraction of its AC impedance,
is generally 2 or more times larger than the corresponding fraction looking
into the primary of a headphone-loaded transformer. This goes part
way towards equalizing the AC and DC impedance of the diode output load.
-
Here is an interesting point of information: The exact frequency
to which the CSUT is tuned is a function of the input level. Reason?
For small signals, the voltage across the diode is rather small, it is
reverse biased for about 1/2 the RF cycle, and the average junction capacitance
is close to the zero bias capacitance. When a large signal is present,
the diode tends toward peak detection and is reverse biased for more than
1/2 the RF cycle. The average back voltage during this period is
higher than when small signals are applied. Since the junction capacitance
reduces when reverse bias increased, the average bias over one RF cycle
is less than it is for small signals. Thus, when the signal level
applied to a CSUT is increased, the frequency to which it is tuned also
increases. All semiconductor diodes exhibit some of this varactor-type
behaviour.
-
If the receiving antenna has a different internal resistance than the 25
Ohms used in the AMCS dummy antenna, the calculated values of S11 and VSWR
and IPL will be in error. I may develop a simple way to measure the
input resistance of a CSUT and will add it to this article if I do.
Published: 07/21/00; Last revision: 04/14/01 |