|
How to Determine the Effective Impedance of a
By Ben H. Tongue
Quick Summary: This article describes a way to determine the effective average impedance of a pair of headphones or a speaker. This is the optimum resistance with which to drive the headphones or speaker to obtain the maximum possible volume. The magnitude of headphone or speaker impedance varies widely over the audio frequency range, being partly resistive and partly reactive. A 'Fixed Insertion Loss Variable Output Resistance Attenuator' (FILVORA) can be used to indicate the effective average value of this impedance, over that frequency range. The first section of this Article refers to the measurement of mono headphones and individual speakers by using a FILVORA. The second section describes how to use the FILVORA to determine the effective average impedance of each element in a stereo headset. The third section describes how the FILVORA was designed. Section 1. |
|
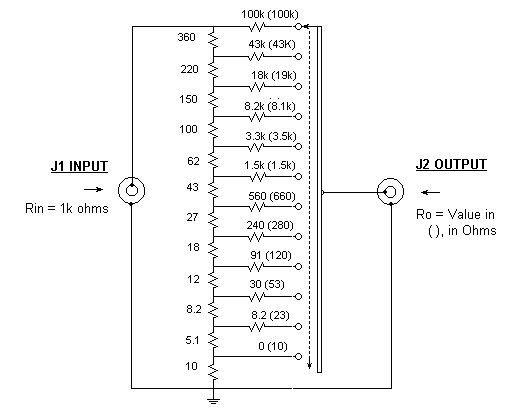 |
|
 |
 |
|
The circuit shown above has a fixed input resistance of 1000 ohms +/- about 5%, no matter what load is connected the output or where the switch is set. The output resistance at any switch point is about +/- 5% of the value shown with any impedance driving the input. The insertion loss of the FILVORA is 26 dB. Standard 5% tolerance resistors are used. To use the FILVORA, connect a source of audio voice or music to the input jack J1. (I use the output jack of a transistor radio for my source.) Connect the plug of the mono headphone set or speaker to be measured to the output jack J2 of the FILVORA. Adjust the switch for the loudest volume. The correct setting indicates the average impedance is very broad and somewhat hard to determine. Call it P2. Rotate the switch in one direction from P2 for a small reduction in volume to position P1 (generally a two positions movement), then in the other direction from P2 by two positions to P3. If the volume at P1 and P3 are the same, P2 indicates the average impedance of the headset. If the volume at P1 and P3 is not the same, increment both the P1 and P3 settings ccw or cc by one position. When you obtain the same volume at the new P1 and P3 positions, you are done. The average headphone impedance is the calibration indication of the switch at point P2. Sometimes equal volume settings cannot be obtained with switch settings five positions apart. If this is the case, try to get equal volume settings four positions apart. If this is done, the average impedance is equal to the geometric mean of the settings of P1 and P3. (Take the square root of the product of the calibration readings at P1 and P3.) It is interesting to note, that with magnetic elements, setting the switch to a high source resistance tends to emphasize the treble and reduce the bass response, compared to the response where the source matches the average impedance of the element. Setting the switch to a low resistance does the reverse. This setting rolls off the highs, and relatively speaking, emphasizes the bass.. With ceramic or crystal elements, a high source resistance tends to emphasize the bass response. A low source tends to roll it off. If you are interested in DX reception with headphones and do not have normal hearing, you might want to customize the optimum source resistance for driving your headphones. This enables using the change in headphone frequency response as a function of headphone driving resistance to partially compensate your own hearing loss curve. Input a voice signal and reduce its volume to a sufficiently low level such that you judge you understand about 50% of the words. Readjust the switch to see if you can obtain greater intelligibility at another setting. If you can, this new switch setting indicates the source resistance with which to drive your headphones to deliver maximum voice intelligibility for your ears. I call this resistance: Personalized Headphone Impedance (PHI). Two FILVORA units enable one to compare the actual power sensitivity
of two headphones, even if the impedance the two headphones are very different.
A dual unit (DFILVORA) is described in Article #3.
Section 2. The impedance of hi-fi stereo headphones may be checked with the FILVORA.
The average impedance of the two earpiece elements can be checked
by determining the switch position for maximum volume with one of these
connections: (1) The sleeve, to the ring and tip in parallel or (2)
the ring to the tip. Measurement (1) will show one half the average
impedance of one earpiece and measurement (2) will give a reading of two
times the average impedance of one element.
Section 3. To create the equations used to calculate the the resistor values for the asymmetrical attenuator 'FILVORA' (it's a minimum loss attenuator at the 100,000 and 10 ohm switch positions), I set up the following requirements:
Comments on points 1-4 above:
|
|