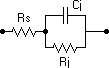
1.  An explanation as to why some diodes that work well in the Broadcast Band result in low sensitivity and selectivity when used at Short Waves:  The parasitic (approximately fixed) series resistance Rs of a diode is in series with the parallel active elements. The non-linear active elements are the junction resistance Rj, which is a function of current through the diode, and the junction cpacitance Cj, which is a function of the voltage across it.

The parasitic series resistance of a 1N34 is pretty high, and in series with the junction capacitance, makes that capacitance rather low Q at high frequencies. That capacitance is, in a crystal set, effectively across the RF tank. The tank usually has a small value tuning capacitor itself, so the overall tank circuit Q is reduced at high frequencies. This is why diodes having Rs and Cj perform poorly at high frequencies. 

2.  An explanation of the meaning and use of dB and dBm:  In the acronym dBm, "d" means one-tenth.  "B" refers to the Bel and is named after Alexander Graham Bell.  The Bel is used to express the ratio of two powers, say (Output Power)/(Input Power).  Let's call this power ratio "(pr)".  Mathematically, a power ratio, expressed in Bels, is equal to the logarithm of the ratio of the two powers.  B=log (pr).  If the two powers are equal, the power ratio expressed in Bels is 0 B.  This is because the log of one is zero.  Another illustration:  Assume that the power ratio is twenty. (pr)=20.  The logarithm of 20 is about 1.3. This power ratio in Bels is 1.3 B.  One decibel is equal to 0.1 Bel.  That is, 10 dB=1 B.  If we express the two power ratios mentioned above (1 and 20) in dB, we get 0 dB and about 13 dB.

So far, we have seen that the decibel is used to express the ratio of two powers, it is not a measure of a power level itself.  A convenient way to express an actual power level using dB is to use a standard implied reference power for one of the powers.  dBW does this.  It expresses the ratio of a power to the reference power (One Watt in this case).  dBm uses a reference power of one milliwatt.  A power level of, say 100 milliwatts, can be said to be a power level of +20 dBm (twenty dB above one milliwatt).  Why?  (100 milliwatts)/(1 milliwatt)=100.  The logarithm of 100 is 2.  10 times 2 equals 20.

The convenient thing about using dB comes from a property of logarithms:  The logarithm of the product of two numbers is equal to the sum of the logarithm of each number, taken separately.  An illustration:  If one has a power source of, say 2.5 mW and amplifies it through an amplifier having a power gain of, say 80 times, the output power is 2.5 X 80=200 mW.  2.5 mW expressed in dBm is +4 about dBm.  A power gain of 80 times is about +19 dB.  The output power is 4+19=+23 dBm.

3.  Maximum Available Power:  If one has a voltage source V with the inaccessible internal resistance R, the load resistance to which the maximum amount of power (Pa) can be delivered is itself equal to R.  Pa is called the “maximum available power” from the  source "V, R.  Any load resistance other than one equal to the source resistance R will absorb less power.  This applies whether the voltage is DC or AC (RMS).  The formula for power absorbed in a resistance is "voltage-squared divided by resistance".  In the impedance matched condition, because of the 2 to 1 voltage division between the source resistance and load resistance, one-half of the internal voltage V will appear across the internal source resistance.  The other half will appear across the load resistance.  The actual power absorbed by the load will be, as indicated in the preceding relation: P = ((V/2)^2)/R = (V^2)/(4R).  Again, in the impedance matched condition, the total power delivered to the series combination of source and load resistance is divided up into two halves.  One half will be unavoidably lost in the internal source resistance.  The other half will be delivered as "useful output power" to the load resistance. Note:  In the crystal radio case the input voltage is AC RF voltage.  If the input voltage is referred to by its peak value as it is in SPICE, instead of by its RMS value, the equation changes.  The RMS voltage of a sine wave is equal to the peak value of that wave divided by the "square root of 2".  Since the power equation squares the voltage, the equation for the “available input power” changes to P = (V^2)/(8R).  This is the equation that is used to calculate available input power from the V, R power source, when that source is a sine wave.

The 'maximum available power' approach is useful when measuring the insertion power loss of two-port devices such as transformers or amplifiers, which may not exhibit matched impedances.  If the V,R source is connected to a resistive load (Ro) of value (equal value) 'R' ohms, it will receive and dissipate a power of Pa Watts.  This is the max. available power, so we can say we have a 'no loss' situation.  Now, assume that a transformer is inserted between the V,R source and Ro, and that a voltage Vo is developed across Ro.  The output power is (Vo^2)/Ro.  The 'insertion power loss' can now be calculated.  It is: 10*log (output power)/(input power) dB.  After substituting terms, it becomes: Insertion power loss =10*log ((Vo/V)^2)*(4*R/Ro) dB. 

4.  Diode Saturation Current and Ideality Coefficient:  Saturation current is abbreviated 'Is' in all of these articles.  Assume that a DC voltage source is connected to a diode.  The polarity of the voltage source is such as to bias the diode in the back direction.  Increase the voltage from zero.  If the diode obeys the classic Schottky equation exactly, the current will start increasing, but the increase will flatten out to a value called the "saturation current" as the voltage is further increased. That is, as the voltage is increased, the current will asymptotically approach the "saturation current" for that diode.  A real world diode has several mechanisms that cause the current to actually keep increasing somewhat and not flatten out as the back direction voltage is further increased.  Diode manufacturers characterize this as reverse breakdown and specify that the back current will be less than a specified value, say 10 uA at a specified voltage, say 30 V, called the "reverse breakdown voltage".  BTW there are other causes of excessive reverse current that are collectively referred to as reverse bias excess  leakage current.  Some diodes have a sharp, controlled increase in reverse current at a specified voltage.  These diodes are called "Zener" diodes.

Is is the very important main parameter that determines the actual diode forward current when it is forward biased by at particular DC Voltage.  Id = Is*(e^(Vd/(0.026*n)-1) at room temperature.  This expression ignores the effect of the parasitic series resistance of the diode because it has little effect on the operation of crystal sets at the low currents usually encountered.  Here Id is the diode DC current, e is the base of the natural logarithms (2.7183...),  ^ means raise the preceding symbol to the power of the expression that follows (Sometimes e^ is written 'exp'), * means multiply the preceding and following symbols, Vd is the Voltage applied across the diode and n equals the "Ideality Coefficient" of the diode (At low uA or high nA currents, most detector diodes have a n of between 1.05 and 1.2).  The lower the value of n, the higher will be the weak signal sensitivity.  One can see that Is is a 'scaling factor' for the actual curve generated by the factor (e^(Vd/(0.026*n)-1).  The value of Is determines the location of the apparent 'knee" on a linear graph of the diode forward Current vs. forward Voltage. (See Article #7.)

Here are a couple of reference points of information.  Typically, if a diode is biased at 0.0256*n Volts in the forward direction, it will pass a current of 2 times its Is.  If a diode is biased at 0.0182*n volts in the reverse direction, it will pass a current of 0.5 times its Is.  As mentioned earlier, n is usually between 1.05 and 1.2.  The 1.05 value usually is about correct for silicon Schottky diodes (not silicon junction diodes).  I have found that the a value of between 1.1 and 1.2 is usually correct for germanium diodes when the current is low, say, at or below 20 times Is.  An easy way to determine the approximate value of Is can be found in Article #4, section 2. 

5.  Explanation of why, in a diode detector operating at high signal levels, the input RF resistance approaches a value equal to one-half the output audio load resistance, and the audio output resistance approaches two times the RF source resistance:  Consider first, a diode detector that is well impedance-matched both at its input and its output when driven by a very low power RF input signal.  This impedance will be: Rd = 0.026*n/Is.  (See part 3 above for a definition of terms.)  For this illustration, let the diode have an Is of 38 nA and an n of 1.02.  Rd will be 700k Ohms.  The well matched condition will hold if the input power is raised from a low value, but only up to a point.  After that , the match will start to deteriorate. At an input power about 15 dB above that of the square-law-linear crossover point, the match will have deteriorated to a VSWR of about 1.5:1  (VSWR = Voltage Standing Wave Ratio.).  A further increase of input signal power will result in a further increase of VSWR.  This means that the input and output resistances of the detector have changed from their previously matched values.  The input resistance of the diode detector decreased from the value obtained in the well impedance matched low power level situation.  The output resistance increased. The reason for this change is that a new law now governs input and output resistance when a diode detector is operated at a high enough power level to result in a low detector insertion power loss.  It now operates as a peak detector.  The rule here is that the CW  RF input resistance of a diode peak detector approaches ½ the value of its output DC load resistance.  Also, the audio output resistance approaches 2 times the value of the input AC source resistance.  Further, since the detector is now a peak detector, the DC output voltage is the "square root of 2" times larger than of the applied input RF RMS voltage. (It's equal to the peak value of that voltage).  This relationship is necessary so that in an ideal peak detector, the output power will equal the input power (No free lunch).  If we were to adjust the input source resistance to, say 495k Ohms (reduce it by sqrt2) and the output load resistance to 990k Ohms (increase it by sqrt2) by changing the input and output impedance transformation ratios, the insertion loss would become even lower than before the change and the input and output impedance matches would be very much improved (when signal levels are high).

A good compromise impedance match occurs if one sets the RF source resistance to 0.794*Rd and the audio load resistance to 1.26*Rd.  With this setup, theoretically, the impedance match at both input and output remains very good over the range of signals from barely readable to strong enough to produce close to peak detection.  A measure of impedance match is "Voltage Reflection Coefficient", and in this case it is always better than 18 dB (VSWR better than 1.3).  Excess insertion loss is less than 1/3 dB and selectivity is largely independent of signal level.

Here is an interesting conceptual view of a high signal level diode detector circuit:  Assume that it is driven with a sufficiently high level sine wave voltage so it operates in its peak detection mode, and is loaded with a parallel RC of a sufficiently long time constant..  This detector may be thought of as a low loss impedance transformer with a two-to-one impedance step up from input to output, BUT having an AC input and a DC output, instead of the usual AC input and output.   The DC output power will approximately equal the AC input power and the DC output voltage will be about sqrt2 times the RMS AC input voltage.

6.  Some misconceptions regarding Impedance matching and Crystal Sets:  To understand the importance of impedance matching, one must first accept the concept of "power".  A radio station accepts power from the mains and converts some of it to RF power which is radiated into space.  This power leaves the transmitting antenna at the speed of light and spreads out as it goes away from the antenna.  One can prove that power is radiated by substituting a LED diode for the regular diode, getting physically close enough to the station and then tuning it in.  The LED will light up (give off light power), showing that some power is being broadcast and that it can be picked up. Now back at home, if one tunes in the station one gets sound in the headphones.  What activates one's hearing system is the power of the perceived sound.  BTW, if one gets too much sound power in the ear for a long enough time, the power can be strong enough to break off some of the hair cells in the inner ear and reduce one's hearing sensitivity forever.  The theoretical best one can do with a crystal set setup is the following:  (1) Use an antenna-ground system to pick up as much as possible of the RF power passing through the air in its vicinity .  In general, a larger antenna will pick up more power from the passing RF waves than will a smaller one.  (2) Convert the intelligence carrying AM sideband RF power into audio electrical power.  (3) Convert the electrical audio power into sound power and get that power  into the ear.

There are power losses at each of the three steps and our job is to minimize them in order to get as much of the sideband RF power passing through the vicinity of the antenna (capture area)  changed into audio power for our ears.  When the "available power" at the antenna-ground system is directed to the crystal set input, we want it all to be absorbed into the crystal set then  passed on through it to our headphones as sound.  If the input impedance of the crystal set is not "impedance matched" to the impedance of the antenna, some of the RF power hitting the input to the crystal set will be reflected back to the antenna-ground system and be lost.  See Article # 15 for updated information on this.

An impedance-matched condition occurs when the resistance component of the input impedance of the crystal set equals the "source resistance" component of the impedance of the antenna-ground system.  Also, the reactive (inductive or capacitive) component of the impedance of the antenna-ground system must see an opposite reactive (capacitive or inductive) impedance in order to be canceled out.  In the impedance-matched condition, all of the "maximum available power" (See section on "Maximum Available Power" above) intercepted by the antenna-ground system is made available for use in the crystal set and none is reflected back towards the antenna to be lost.

Now we are at the point where confusion often exists:  The voltage concept vs. the power concept.  Let's assume that the diode detector has a RF input resistance of 90,000 Ohms.  Assume that the antenna-loaded resonant resistance of the tuned circuit driving it is 10,000 Ohms.  If one uses voltage concepts only, one might think that this represents a low loss condition.  After all,  9/10 of the actual source voltage is actually applied to the detector. NOT SO!  If one now impedance matches the source RF resistance to the diode RF resistance via RF impedance step-up transformation (maybe tapping the diode up to a higher point on the tuned circuit), good things happen.  (We will assume here that, in the impedance transformation to follow, the ratio of loaded-to-unloaded Q of the tuned circuits is not changed.)   For an impedance match, the tuned circuit resonant resistance should be transformed up by 9 times.  If this was done by a separate transformer (for ease of understanding) it would have a turns ratio of 1:3, stepping up the equivalent source voltage by 3 times and changing the equivalent source resistance to 90,000 Ohms.  What now?  Before matching, the diode got 9/10 of the source voltage applied to it.  Now it gets 1/2 the new equivalent source voltage (remember the equivalent voltage is 3 times the original source internal voltage).  The 1/2 comes from the 2:1 voltage division between the resistance of the equivalent source of 90,000 Ohms and the detector input resistance of 90,000 Ohms.  The ratio of the new detector voltage to the old  is: 3 times 1/2 divided by 0.9 = 1.67 times.  This equates to a 4.44 db increase in power applied to the detector.  If the input signal to the detector is so weak that the detector is operating in the square-law region, the audio output power  will increase by 8.88 dB!  This is about a doubling of volume.

7.  Caution to observe when cutting the leads of a glass Agilent 5082-2835 Schottky diode (or any other glass diode):  When it is necessary to cut the leads of a glass packaged diode close to the glass body, use a tool that gives a scissors type of cut.  Diagonal cutters give a sudden physical shock to the diode that can damage its electrical performance.  This physical shock is greater than one might expect because of the use of plated steel instead of  more ductile copper wire. Steel is used, in part, because of its lower heat conductivity, to reduce the possibility of heat damage during soldering.

Published: 04/25/00;  Last revision: 08/20/01