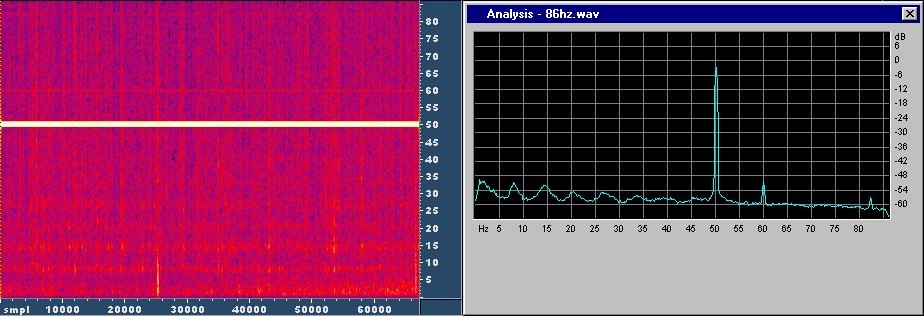
Renato Romero sent me a copy of a recording containing Schumann resonances. So I want to thank him for that first. The recording was made with his big electric vertical field antenna and also contained a 50Hz main power tone, a 60Hz oscillation from PC monitor vertical crt deflection and a 82Hz carrier for Russian submarines :

Removal of the 50Hz, 60Hz and a 82Hz lines was no problem with Cool Edit using FFT Filters:

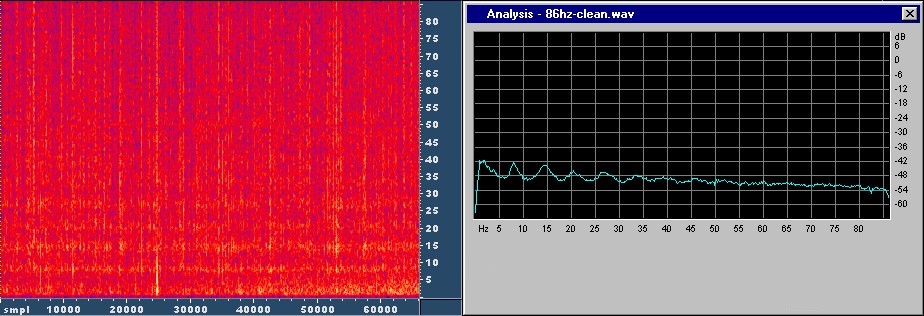
Then my thought was this: The Schumann resonance occur, because the waves are travelling around the earth and they must be essentially something like echoes. This fits to the frequency pattern of those bands, beeing roughly
"overtones" of a commom fundamental. So if there is some portion of periodicity at a repetition rate about 7Hz, this is what distinguishes it from signals of other origin. Knowing this I looked for autocorrelation with a time offset of 1/7 second between the original and a delayed wave.

So I made a copy of the wave, added silence of 1/7 second to the beginning and performed a multiplication of those waves with each other. Moments of high correlation must show a positive result, no correlation zero and anti-
correlation a negative result. After that the resulting wave was filtered by a low pass of ~1 Hz, normalised and then mutiplcated with the original. The resulting wave then was low in mean amplitude, with some spikes at those moments, when correlation was very high or low. This was then added to the original signal, thus weakening the parts with negative correlation and enhancing those with a high positive one. As you can see, some "bad" signals are indeed weakened and the spectrum is improved (the Schumann ripple is slightly enhanced):

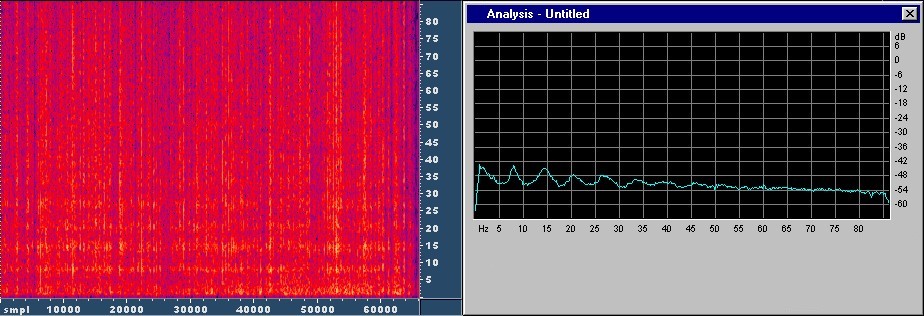
The last experiment was to eliminate those parts of the wave that contained high amounts of frequencies above 35 Hz, as such signals are also not commom to schumann resonances. The steps were similar: High pass, self- multiplication in order to get a positive signal indicating amplitude, low pass filter, multiplication with signal, subtraction from signal. After blanking the parts with strong portions of  f > 35Hz  it looks like this:

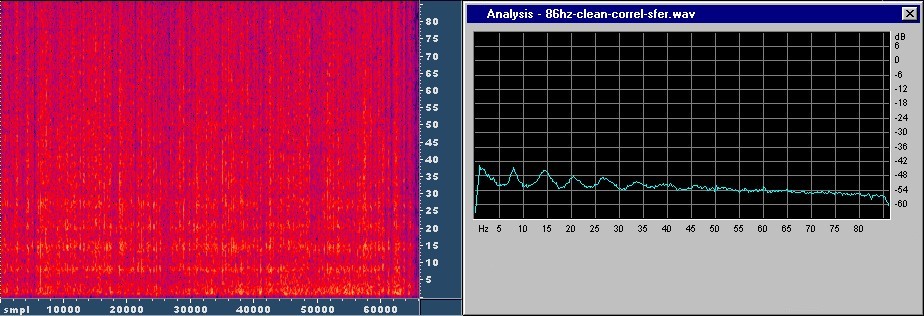
Indeed, those parts of the wave containing high frequency components were weakened, but the spectrum didn't improve further and what remained still contained a lot of noise. This shows, that even sferics from near sources contribute to the Schumann resonances.

So what we can do whith the schumann resonances ist to produce a measure of strength by applying an autocorrelation function. DC removal is necessary for this and low pass filtering / hum removal is recommended.
I don't know, wether the Q-bursts are of any interest, but a plot of mean intensity can be obtained and recorded in a long-time measurement with very low data rate.

What is needed for this task is: A/D conversion, digital delay of 1/7 second, multiplication of original with delayed signal and lowpass filtering. The analog way then needs a D/A converter, a mixer and a lowpass. As data aquisition and storage will probably be digital again, it makes more sense to skip the intermediate analog part and perform the multiplication and filtering using DSP algorithms.