Ian Purdie's Amateur Radio Tutorial Pages

Low Pass Filters Design

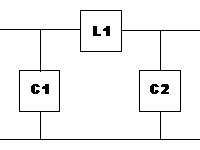
We will start with low pass filters ( LPF ) because they are the basis of other filter designs. High pass or bandpass filters are often simply transformations from low pass filter designs.

Perhaps the simplest low pass filter is the classic butterworth pi network design where the reactive elements are of a constant impedance e.g. 50 ohms and the design Q = 1.

This example is most frequently used in the output of a transmitter to minimise harmonic output and eliminate QRM. As with all simple designs there is a limit to the benefit to be gained. If such a filter were designed with a cut off (Fc) of 7.5 Mhz the attenuation only becomes significant well away from that frequency.

It is simply two L networks added together like this:

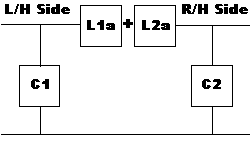
Where C1 = C2 = 50 ohms each and L1a = L2a = 50 ohms each or a total of 100 ohms.

The attenuation of this particular filter is given by the equation:

A_db = 10 log [ 1 + ( W / W_c ) ²ⁿ ]

• W = the frequency of desired attenuation
• W_c = the cutoff frequency ( W_3db ) of the filter
• n = the number of elements in the filter

For our three ( n  ) element filter above with a  W_c of 7.5 Mhz and checking out the first harmonic ( W ) at 15 Mhz  we find the attenuation at 15 Mhz is a mere 18.13 dB.

Obviously you would not get over excited by that number yet it is a fact of life. How many of you have thought such a LPF would yield stunning results?.

A good example to investigate is the same filter used as the input to a receiver with an IF of 455 Khz. Our local oscillator runs at 7500 Khz + 455 Khz or 7955 Khz. An image frequency would be at 8410 Khz. Believe it or not I've seen serious attempts at receiver design using such a very casual approach.

Slotting the image of 8.410 Mhz into the above equation gives an attenuation at that frequency of only 4.75 db. If you don't believe me check it out yourself ( which as an aside, you should be doing anyway). Considered in another light - no IF filter is ever going to remove your image interferer.

O.K. well what is the use of such a filter?. Firstly if you consider reducing interference to the low VHF TV band you can get acceptable performance. Do a calculation of the attenuation at 50 Mhz. Secondly the filter is excellent ( in my humble opinion ) as an impedance converter or matching device. In this circumstance I consider any attenuation benefits accruing to be entirely a bonus.

Again back to the simple 3 pole filter we used above. At any design frequency the reactances for 50 ohms input / output impedance always  remain 50 ohms. L1 is 100 ohms and C1 and C2 are also both 50 ohms. At 7.5 Mhz these reactances become C1 = C2 = 424 pF and L1 = 2.12 uH.

Now here comes a very sneaky trick called Bartlett's Bisection Theorem. I have no idea who Mr. Bartett was, where he came from or when he discovered this trick. All I know is that I read about it somewhere and I was so impressed it has stuck in my mind.

In the above example Zin = Zout = 50 ohms and C1 = C2 = 50 ohms and L1  = 100 ohms. Which is the same as:

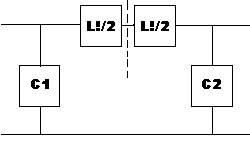
Where we have merely split the top reactance back in half, i.e. L1 becomes 1/2 L1 + 1/2 L1 or 50 ohms + 50 ohms. Logical eh!, we've returned to the two back to back L networks.

Assume you wanted to match 50 ohms to 200 Ohms. Okay L/H side remains static at 50 ohms and convert the R/H side to 200 ohms by multiplying the reactances by  200/50. This has the net effect of multiplying R/H inductances by 4 and dividing R/H capacitances by 4. In our example C1 remains 50 ohms C2 is now 200 ohms and L1 has become 250 ohms. At 7.5 Mhz C1 remains 424 pF C2 has become 106 pF and L1 = 5.3 uH. Therefore we have a matching network and some harmonic attenuation.

Remember that these filters ARE bilateral, this means either side can be used as input or output according to your requirements.

Also remember the above design of two back to back L networks had a design Q of 1. You would soon find this is somewhat restrictive. A better approach is to have both L networks match a mythical centre or invisible resistance which is called "virtual resistance" or creatively R.

The transformation from double-L to Pi networks

We will for our purposes use a loaded Q or QL which equates to:

Q = ^{[  ( Rh / R ) -1 ]}

R = R_h / ( Q² + 1 )

BUT  Q must exceed [ ( R_highest  / R_lowest ) -1 ]

Assume in our earlier example where Q =  1 and R_s = 50 ohms and R_L = 200 ohms.

Here Q must exceed 1.732 so we will use a typical amateur Q figure of 3. Then R would become R_h / ( Q² + 1 ) or 200 / 10 or 20  i.e. R = 20  and:

Zin = 50 ohms                                              Z out = 200 ohms

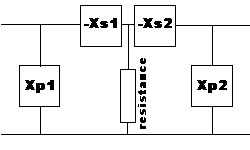
Figure 4.

For the R/H or Load side
Xp2 = Rp / Qp = R_L / Q = 200 / 20 = 10 ohms
Xs2 = Q *  R_series  = 1 * 20 = 20 ohms

For the L/H or Source side
the Q₁ here is the ratio of Rs to R or;

Q₁ = ^{[  ( Rs / R ) -1 ]}

Q₁ = ^{[  ( 50 / 20 ) -1 ]}

Q₁ = 1.2247    AND;
Xp1 = Rs / Q₁ =  50 / 1.2247  =  40.83 ohms
Xs1 = Q₁ *  R_series  = 1.2247 * 20 = 24.494 ohms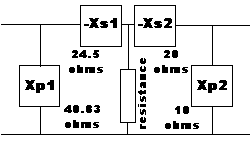

Figure 5.

Just exactly how useful is all this information

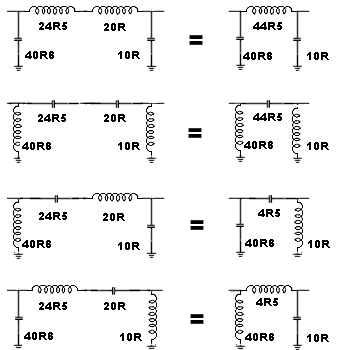
Each of the four reactances we have calculated can be either an inductor OR a capacitor. The only aspect you must remember is that the X_p's and X_s's are  of opposite types or signs and add or subtract accordingly.

From this we can obtain four different networks. Everything is shown as reactances and I have omitted source and load impedances.

The first network is obviously a low pass filter. The second becomes a high pass filter the other two exhibit high or low pass characteristics. Do you use the configuration on the left or the configuration on the right?

This will entirely depend upon individual circumstances, availability of components etc. and in particular the need to sometimes include a variable element in your circuit. Other times you may wish to include the inductor in the collector of your circuit and need a blocking capacitor to the next stage. This scenario however must take into account the effect circuit strays and transistor capacitance would have on your design and its' subsequent response.

Let's look again at our previous oscillator circuit. If you are unfamiliar with oscillators then review my previous oscillator tutorial. It will certainly help you.

Clearly this would really lead us on to the topic of bandpass filters.

The circuit configuration presented here is only one of the 1000's of differing types and configuations available.

the author Ian C. Purdie asserts the moral right to be identified as the author of this web site and all contents herein. All rights reserved. See copying and links. These electronic projects are provided for individual private use and the author assumes no liability whatsoever for the application, use, misuse, of these projects that result in the direct or indirect damage or loss that comes from these projects. All materials are provided for free private and public use. Commercial use prohibited without prior written permission from Ian C. Purdie.