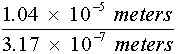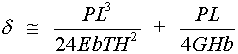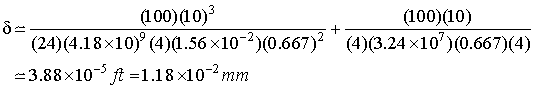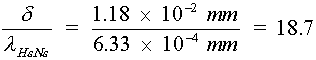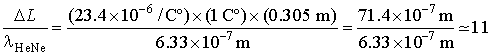|
Module 6-1 OPTICAL TABLES AND BENCHES © Copyright 1987 by The Center for Occupational Research and DevelopmentAll rights reserved. No part of this book may be reproduced in any form or by any means without permission in writing from the publisher. The Center for Occupational Research and Development Printed in the U.S.A. ISBN 1-55502-024-0 (1) In electro-optical laboratory environments, few considerations are more critical than the way optical components and associated equipment are mounted. (2) In Module 6-2, "Component Support," we’ll discuss the actual devices that are used to mount components such as mirrors, lenses, prisms, and diffraction gratings. In this module we will focus our attention on the surface on which the optical mounts are affixed. We will direct most of our discussion toward the requirement of nonpermanent optical assemblies. Most of the optical assemblies that you’ll construct in research laboratories are of the "experimental" nature. They are meant to be dismantled after serving a particular purpose. Permanent optical assemblies, such as the optics in a supermarket bar-code scanner, are custom-designed. They are not part of our discussion—although most of the same principles that we’ll discuss still apply. (3) The main purpose of this module will be to help you to make a reasoned judgment of what type of device to select as the "foundation" of a particular optical system. Depending on the particular geometry of an optical setup, various options will be more favorable than others. (4) For example, if you need to assemble an optical system that lies along a single straight axis, an optical rail or optical bench might be an appropriate choice on which to attach the various optical mounts. On the other hand, if the optical setup will by necessity occur in a plane, or even several planes, then an optical table or optical breadboard will usually be a more convenient choice. (5) We’ll also discuss the major requirements of critical optical assemblies such as mechanical and thermal stability and vibration isolation. Most of our discussion will be about modern optical benches, tables and breadboards that have become de facto industry standards in laboratories that use lasers and related optical and electro-optical apparatus. (6) Before you start this module, you should understand algebra, general laboratory and electrical safety, waveform analysis, and the use of transducers, oscilloscopes and low-power helium-neon lasers. 
(7) When you complete this module, you should be able to do the following.
DISCUSSION Optical Benches (8) An optical bench—sometimes called an optical rail—gives a stable, inline surface where optical system components and supports can be installed and adjusted to various relative positions and then held rigidly in place. The optical bench is most useful when the optical axis of the experimental arrangement or system lies along a straight line or in a vertical plane. (9) Technicians use most optical benches for one or more of these applications.
(10) In each case the bench or rail is the stable base on which you mount the component supports. The mounting devices are called "carriages." The component support is mounted either directly onto the carriage or at an adjustable height above the carriage on a rod. These elements are all shown in Figure 1.
Fig. 1. (11) This description of optical rails or benches will be divided into four broad types: Lightweight aluminum rails H-beams Triangular rails Flat-bed or "lathe-bed" benches (12) Generally speaking, this list is shown in increasing order of quality and expense. You can get a good-quality one-meter-long aluminum rail for less than $200. But, certain complete flat-bed systems will cost more than $60,000. (13) The quality of an optical bench is measured in terms of how well it satisfies these two questions:
Lightweight Aluminum Rails (14) A typical example of a lightweight aluminum rail is shown in Figure 2. Stock lengths of rail are available from about 15 centimeters up to two meters, with either English or metric mounting holes. Attached to the rail are two typical carriages or carriers that accept rod-mounted optical components. (15) Aluminum rails like these usually are designed with slotted mounting holes to allow secure attachment to optical tables, as shown in the figure. Many manufacturers also provide coupling plates so that two or more optical rails can be firmly attached at various angles to accommodate optical setups that require more than a single axis. (16) A variety of carriages are also available. The carriages let you mount a wide variety of components and equipment such as lens holders, translators and rotators. A more complete discussion of these mounts is in Module 6-2.
Fig. 2
(17) For added convenience, many optical rails have linear scales running along their length. The linear scale helps you to position equipment accurately. Vernier scales are also often attached to the carriages. These give an even more accurate determination of the position of components mounted on the rail. H Beam (18) An H-beam optical bench is used for rugged breadboards of heavy electro-optical or laser systems. One is shown in Figure 3a. (19) The bench is made from a structural H-beam of either steel or aluminum. Channel often is used also. The top surface is milled flat. Components are either bolted down to the H-beam or held rigidly with C-clamps. (20) The H-beam bench is relatively inexpensive and can be made in the shops. Its main disadvantage is that elements can’t be translated along the beam and remain in optical alignment. However, where you need this feature, you can modify an H-beam bench as shown in Figure 3b by milling edges and clamping the component to the side with a setscrew.
a. Laser breadboard on H-beam bench with C-clamps to hold component supports.
b. Modified H-beam bench to maintain component alignment during translation. Fig. 3
(21) In the early days of the laser industry, such "homemade" optical rails were quite common. In many cases, the optical components were held in mounts, affixed to the H-beam with double-sided tape! With the improved convenience and availability of commercial aluminum rails and ferro-magnetic optical tables and breadboards, such improvised mounting systems are an increasingly rare sight in industrial and university laboratories.
Triangular Rail (22) A triangular optical rail (Figure 4) is the most widely used optical bench. The rail usually is made of aluminum, cast iron, or steel. It has an equilateral triangular cross section (about 2 inches per side) with grooves on the two top sides. The rails can be made straight to 0.005 inch. The grooves running down the length of both sides are used to lock the carriages in place with a screw. (See Figure 1.) Triangular benches are fixed directly to optical tables. Or, they’re mounted on cross-feet for precise leveling.
Fig. 4
Flat-bed Benches (23) Flat-bed optical benches (Figure 5) offer the ultimate in rigidity and straightness in an optical bench. They can be made from high-grade stainless steel or granite. The bed usually has a dovetail cross section for accurate, stable guiding and clamping of optical carriages. The benches are extremely heavy and expensive—they’re used for very special applications where high precision is required.
Fig. 5
Thermal Effects on Bench Length (24) Spacing between elements mounted on an optical bench varies if the temperature changes cause the length of the bench to change. This is due to thermally induced expansion and contraction of the bench material. (The following material has been moved here from pages 17 and 18. When a material is heated, it will expand according to the relationship,
Table 1. Typical Values of a
The effect of thermal expansion on laser components attached to a stainless steel table are illustrated in Example A. wavelengths.
(32.3.4) Therefore, the longitudinal modes in the laser cavity will "hop"—in other words longitudinal modes will form, collapse, and reform—about 33 times as the optical table heats up. If we monitored the output of the laser with an optical power meter, we’d notice a periodic fall and then rise in the laser output. (32.3.5) In laboratories where thermal stability is particularly important the optical tables often are made of Invar, a low-expansion alloy whose expansion coefficient is only –0.20 ´ 10–6 °C–1. That’s about 55 times better than typical stainless steel! (End of material moved from pages 17 and 18.)
Care of Optical Benches (25) Optical benches must be cared for to prevent warping, rusting, and nicking. A long bench should be supported from beneath at points approximately every two feet along its length. Such support will prevent the bench from bending under its own weight and the weight of the elements it supports. Use common sense to prevent loading a bench with elements that are too heavy. (26) Since most benches are made of steel, they can rust. Use a coat of light oil—applied sparingly and then wiped off—on the bench and the carriages every several months. Do not use oil on the component supports. (27) Be careful not to hit the bench surface with a carriage or other object. This can cause nicks and grooves that will prevent the carriages from moving smoothly along the surface and will frustrate attempts to maintain alignment.
Aligning a Bench to an Optical Axis (28) Frequently a test will require that an optical bench be aligned parallel to an existing optical axis or light beam. If a laser or light beam defines the optical axis, you accomplish the alignment procedure by using an iris diaphragm or a set of cross hairss mounted on the bench with a carriage. You adjust the bench position until the laser beam passes through the center of the iris (or cross hairs) without perpendicular carriage adjustment at any position along the optical bench. (29) Detailed steps for carrying out the alignment procedure, using a laser and a set of hairs, are outlined below: 1. SECURELY position the laser to establish an optical axis. Most benches are designed to be aligned to a horizontal axis, so try to establish the laser beam axis as close to horizontal as possible. 2. Obtain in index card and draw a set of perpendicular "cross hairs" in the center of the card. 3. Position the optical bench roughly so that it appears to be parallel below the laser beam. Move all adjustment screws to the center position of their turning range. 4. Center and secure the card to a mount such that the laser beam or the cross hairs is centered when the mount is placed on the far end of the bench. Do not secure the mount to the bench since it will be moved from one end of the bench to the other. 5. It is very important not to change the position of the card with respect to the mount any more after this! Whenever the card is to be moved, the bench mount containing the card must be moved with it. 6. Move the mounted card to the near end of the bench. If the laser beam does not center on the cross hairs, turn the adjustment screws on the bench until it does. 7. Move the card to the other end of the bench. The laser beam should center on the cross hairs. If it does not, turn the adjustment screws on the bench. 8. Repeat steps 6 and 7 until you no longer have to touch the adjustment screws to line the laser beam up with the cross hair--on either end of the bench.
When Does an Optical System Require (30) A table (Figure 6) is desirable for breadboarding an optical system, test or experiment if any one or more of the following conditions exists or is required.
(31) Typical examples of applications where you should use optical tables are listed below.
Fig. 6
Fig. 7
4. Electro-optical systems development (examples: IR scanner, scanning imaging spectroradiometer, star trackers, laser radars). Requires support of massive components, stability, location of electronic, and thermal equipment immediately adjacent to the optical setup. See Figure 8.
Fig. 8
Desirable Characteristics of Optical Tables (32) Generally, an optical table should provide a stable plane surface where optical components and supports can be rigidly placed or moved to any position or angle. The ability of a table to satisfy these requirements depends on the degree to which it has the following characteristics.
Fig. 9 (32.2.4) Figure 10 shows how a table surface will deflect when it experiences a point load at its center. Such a load occurs when heavy equipment—such as lasers and spectrometers—is mounted on the table. (32.2.5) Although equipment doesn’t apply load to the table at a single point, the point-load model is useful in estimating the actual deflection that can be expected. You can figure the additional deflection of the center of a honeycomb table due to a point load at the center from Equation 2.
Fig.10
Fig. 11
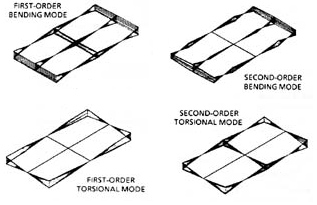
(32.4.3) Bending and torsional modes of the table surface can be reduced greatly in amplitude by constructing the core of the table from an appropriate damping material. Most modern optical tables use various metal honeycombs for this purpose. (32.4.4) Honeycomb construction was developed in great part for use in aircraft construction. Honeycombs provide excellent internal damping. And, they provide good mechanical strength with relatively little weight. Figure 12a shows the response of a 4-foot ´ 10-foot ´ 8-inch solid granite slab to an impulse. Note that after 0.30 second there’s still an appreciable amplitude to the "ringing" of the tabletop. By comparison, a similar impulse is applied to a same-size steel honeycomb tabletop. The resulting "ringing" is damped out in approximately 30 milliseconds (Figure 12b). That’s a dramatic difference in damping rates.
Fig. 12
(32.4.5) Vibrations that result from motion of the laboratory floor usually occur in approximately the 5-Hz to 30-Hz range. Modern isolation optical table systems usually are suspended on pneumatic legs that are designed to resonate mechanically at about 1 Hz when loaded with a tabletop. The mechanical resonance is far lower in frequency than typical floor vibrations. So, little energy is transferred from the floor to the table surface. (32.4.6) The pneumatic isolation support system combined with the metal honeycomb damping materials make modern optical tables an excellent surface on which to conduct vibration-sensitive experiments. For these reasons—in addition to convenience and cost—steel honeycomb table systems with pneumatic supports have replaced solid metal or granite tabletops in most electro-optical laboratories. 5. (32.5.1) Ability to attach a component holder firmly in place. Optical components normally are held by mounts that have precision-flat bases. This allows the experimentalist to slide the base around on the table until the component is positioned correctly. When the mount is in the proper position, it’s desirable to firmly attach it to the table. (32.5.2) As we’ll see in Module 6-2, several methods of attaching mounts to surfaces commonly are used in electro-optical laboratories. The most common types of attachment are: bolts into threaded holes drilled in the table or bench surface, inertial mounts (heavy bases) and magnetically held mounts. Modern honeycomb-construction optical tables and breadboards usually are supplied with a standard pattern of threaded bolt holes and a ferromagnetic upper surface, to facilitate the mounting of components.
Types of Tables—Methods of Fixture Attachment (33) Several types of optical tables are used. Some are very crude (and inexpensive) and some are very elaborate (and expensive). It’s important to know how much quality (flatness, rigidity, vibration isolation and low expansion) you need for a specific application. (34) If an optical system doesn’t require high-precision alignment and stability, it’s economically wasteful to specify a high quality. Conversely, if high-precision alignment and/or stability are required, a crude setup will waste the experimentalist’s time and possibly cause erroneous results. (35) The following list describes most optical tables that are commonly used, along with the method of attachment of fixtures to the table.
a. Laser power measurement on a workbench
b. Laser breadboard on workbench with metal surface plate Fig. 13
Fig. 14
a. Granite table with threaded insert holes
b. Attachment for component support Fig. 15 5. (35.5.1) Metal tables with tapped mounting holes. These tables are used similarly to the granite tables with inserts. Solid metal tables are usually not as thick or expensive as comparable granite tables. In certain electro-optic applications, it may also be desirable to use a metal table so that it can act as an electrical grounding plane for the system electronics. (35.5.2) As we said earlier, most metal (steel or aluminum) tables aren’t solid. They have a metal "honeycomb" core structure covered with a thin metal skin (1/8 inch to 3/16 inch thick). (See Figure 16.) This composition provides increased rigidity and good damping of lateral vibrations.
Fig. 16
(35.5.3) Similar tables are also available that are composed of a phenolic-impregnated paper honeycomb core and solid surface with a matrix of tapped holes. 6. (35.6.1) Smooth metal tables with magnetic mounting. Either solid or honeycomb-core tables are available with smooth working surfaces of ferromagnetic metal. Component supports are attached to these tables by magnetic mounts. (See Figure 17.) (35.6.2) These magnetic bases are switched "on" and "off " by rotating a strong permanent magnet within the base. In the "off" position the magnetic flux travels almost entirely through the metal of the base. In the "on" position, the permanent magnet is rotated so that virtually all of the magnetic flux travels through the table surface. (35.6.3) Depending on their size and cost, such magnetic bases can have holding forces of from 24 to 300 pounds. These bases work best on unpainted, ferromagnetic surfaces (such as type-410 or -430 stainless steel) with a skin thickness of at least 5 mm (3/16 in).
Fig. 17
(35.6.4) This technique should not be implemented where the presence of strong magnetic fields might temporarily distort or destroy an electro-optic component (such as image-converter tube assemblies). 7. (35.7.1) In many applications, excellent vibration isolation isn’t needed, but the convenience of a ferromagnetic mounting surface and predrilled holes is desired. In such cases, optical "breadboards" often are used as a lower-cost alternative to honeycomb isolation tables. Figure 18 shows one example of an optical breadboard.
Fig. 18
(35.7.2) Like honeycomb isolation tables, these breadboards come in a variety of stock and custom sizes and hole patterns. Typical hole patterns are 1/4-20 holes on 1-in centers. But, metric holes (usually M6 on 25-mm centers) are also available. The 2-ft ´ 3-ft breadboard shown in Figure 18 also has a slot along each side to permit equipment to be "hung off " the side using bolts and captive nuts. (35.7.3) Some manufacturers also will finish the breadboard surface epoxy-based semigloss black paint to reduce stray reflections. Such finishes, while attractive, can be fairly easily marred. And they somewhat reduce the holding power of magnetic bases. (35.7.4) If you need some degree of vibration isolation, you can suspend breadboards on firm tabletops with small-diameter inner tubes or sheets of foam rubber. In some cases, these "budget" isolation surfaces make sense as a significantly lower-cost alternative to pneumatic isolation tables. Vibration Isolation (36) As we said earlier in this module, optical tables are susceptible to induced vertical and horizontal vibrations. These vibrations are undesirable in applications that involve very precise optical alignment systems because they result in relative movement between the optical components mounted to the table. (37) You can understand vertical vibrations within the table surface by visualizing a very small, periodic bending motion, or flexing, in the table—similar to a diving board. (See Figure 11.) These vibrations originate as floor or building resonant vibrations. They’re induced through the table supports. The frequencies of these vibrations typically range from 5 to 30 Hz. (38) You can isolate some vibration in a rigid-frame table support by placing rubber pads between the table legs and the floor and between the support and the table surface. You’ll get much more effective isolation by using air pistons in the table legs. (See Figure 19.) These pistons actually "float" the tabletop and provide isolation from vertical floor vibrations. Vibration-isolation systems are similar to a high-frequency cutoff filter, insofar as they pass low-frequency vibrations and isolate all frequencies above some design value. Air pistons provide vertical isolation for frequencies above 5-10 Hz, and generally require a source of compressed air in the laboratory.
Fig. 19 Selecting the Correct Table (39) The design and construction of a vibration-isolated optical table takes considerably more theoretical insight and working experience than we can give you in this module. The important points to learn are: · A general understanding of the kind of performance you can expect of crude and sophisticated optical tables · An estimate of the optical table performance required by the experiment or alignment to be performed · Knowledge of how and what to specify when you need an optical table (40) The lab tasks in this module should provide some experience for the first point. An understanding of the optical experiment or alignment should provide data for the second point. Address the third point by answering these questions: · How much working area do you need? · How accurately must you maintain component spacings? · What maximum temperature variations do you expect in the laboratory? · What degree of table surface flatness is required? · What vibration isolation (if any) is required? How much vibration can be tolerated, and at what frequencies? · Do you need to fasten components rigidly to the table surface? · Would the fields produced by magnetic support attachments distort the operation of the electro-optical system? · Would a conductive work surface (ground plane) be beneficial or detrimental to the electro-optical system operation? · What’s the "long-term" use of the table? How much versatility do you need? · How much money is in the budget for this equipment? (41) Quite often, an early consideration of the last item forces compromises in system requirements for the optical table. 
1. Name four classes of optical benches. List one advantage and one disadvantage of each. 2. Define the following terms:
3. List the advantages and disadvantages (at least two of each) of the following optical tables:
4. In your own words, outline the procedures used in the laboratory to align an optical bench parallel to an optical axis established by a laser beam. 5. Outline the specifications of two optical tables of comparable size. Use the criteria given in the section, Selecting the Correct Table, and catalogs from suppliers of optical tables. From your outline, evaluate the effectiveness of the table in isolating low-frequency vibrations. 6. How much will the center of a 4-ft ´ 8-ft ´ 12-in steel honeycomb table deflect when loaded with a 150-lb spectrometer at its center. Skin thickness is 1/8 inch. The spectrometer applies a point load to the center of the table. Get any more data that you need from the example worked earlier in this module. Express your answer in mm. 7. In an experiment that’s particularly sensitive, you can allow the center of your optical table surface to deflect downward by an additional distance equal to only one wavelength of light (633 nm). Assume that you use the table from Exercise 6 and that the only significant load on the table is a point load in the center. What’s the maximum point load allowed? Express your answer in pounds. 8. During a day of use, the air temperature in an optics laboratory increases by 2.50 C°. Compute the thermal change in length of three 8.00-ft-long optical tables used in the lab. The tables are made respectively of aluminum, type-400 stainless and super invar. Express your answers in multiples of the red HeNe laser wavelength. 
Workbench 2-ft ´ 3-ft ´ 1-in shock-mounted metal plate to fit on workbench 4 rubber shock mounts Pneumatic vibration-isolated optical table, 4-ft ´ 8-ft working surface Baseball or tennis ball Sandbag, about 15-25 pounds of mixed sand and various-sized rocks Aluminum cube, 3-in sides, tapped to accept accelerometer mounting stud HeNe laser Autocollimator/telescope Optical bench Cross target Carriage Accelerometer Oscilloscope 
1. Align an optical bench parallel to a given optical axis defined by a laser beam. Use the technique described in the discussion. 2. Determine the response of a table in each of the three axis directions to an induced vibration.
Fig. 20
b. Adjust the vertical amplifier of the scope for maximum sensitivity (5-mV/cm desired). Set the sweep speed at 0.1 msec/cm. Adjust trigger controls to initiate a sweep when a fingertip is brushed lightly across the top of the accelerometer. Triggering level will be near zero, stability control is Preset, slope control on Internal +, and trigger mode on AC slow. If you can’t adjust the trigger level to activate on the weak signal generated by touching the accelerometer, you can set the trigger mode on automatic. c. Hold the ball accurately 30 cm above the middle of the long edge of the table (point A). Release it (be prepared to catch it on the first bounce) while you watch the scope trace pattern. If possible, reduce room light or shade the scope screen so that you can see a persisting image.d. If the pattern height is less than one or two cm, increase the height from which you drop the ball. Make subsequent drops from the same height. Record this height as (h). e. Examine the scope pattern to estimate the general range of frequencies present. The number of full waves (distance between successive peaks) per centimeter, divided by the time per cm, will give an approximate frequency value. For example: the pattern shown in Figure 21 has about 2.5 full waves in a length of 1 cm. With the sweep rate at 0.1 see per cm, the vibration frequency would be 2.5/0.1–25 hertz. If higher frequencies are indicated by the presence of complex wave forms and fine structure, increase the sweep rate while you excite the table (ball drop) until a measurable and reasonably repeatable pattern is produced. Compute its approximate frequency. Record all data in Data Table 1.
Fig. 21
f. Repeat Steps c, d, and e, releasing the ball from the same height (h) over points B and C on the table. Determine and record frequencies, as well as any significant difference in the amplitudes or number of frequencies identified.g. Set the sweep rate at a lower value, so that the signal amplitude decays to about half its peak height in one sweep. Measure the maximum peak-to-peak height of the pattern. Convert to mV, and record as peak amplitude for that frequency. h. Using a slower sweep, determine and record the time required for the signal to decay to half its peak amplitude. i. Turn the mounting block on its side, so that the accelerometer top is parallel to the long side of the table. The accelerometer now will measure vibration in the Y-axis direction. Record data in Data Table 2. j. Repeat the above procedure after moving the accelerometer to measure vibration in the X-axis direction. Record data in Data Table 3. 3. Determining effectiveness of table in damping floor-induced vibrations X) and value of the drop height. Use these for subsequent drops. d. Determine major resonances in pattern, their peak amplitudes and decay times (half-amplitude decay). Record for each frequency. e. Relocate the accelerometer and block (accelerometer vertical) on the floor near the base at point B or C in Figure 22 or near the legs (point A) of the table support.f. Measure and record accelerometer location. Reduce vertical sensitivity by a factor of 100 (0.5 V/cm). Drop the sandbag on the selected point ( X) from the selected height while you watch the scope pattern. Adjust sensitivity to produce a pattern with peak-to- peak amplitude of 4 to 10 cm.g. Identify and measure major resonances of floor, as you did for the tabletop. Convert peak amplitudes to millivolts. Record all data in a table that you prepare.
Fig. 22
h. Compare floor and tabletop vibrations by computing the ratio of peak-to-peak amplitudes at both floor and table accelerometer locations. This ratio will be a measure of the effectiveness of the table in reducing vibrations of the frequencies observed. 4. If you have time, compare the effectiveness of three different tables in damping floor-induced vibrations. Repeat procedures outlined in Section 3. What’s your conclusion? 
Data Table 1. Accelerometer Adjusted for Z Axis
Data Table 2. Accelerometer Adjusted for Y Axis
Ealing Electro-Optics Product Guide. Ealing Electro-Optics, Inc., 22 Pleasant Street, South Natick, MA 01760,617/655-6029. Melles Griot Opt Guide 3. Melles Griot, 1770 Kettering Street, Irvine, CA 92714,714/261-5600 The Newport Corporation Catalog of Precision Laser/Optics Products. No 100. Newport Corporation (formerly NRC), 18235 Mount Baldy Circle, Fountain Valley, CA 92728-8020,714/963-9811. Oriel Corporation Catalog Vol. I of Tables, Benches. Micropositioners, Optical Mounts. Oriel Corporation, 250 Long Beach Boulevard, Stratford, CT 06497-0872,203/377-8282. Specification sheet and application data on accelerometers. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
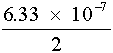meters = 3.17 ´ 10–7 meters
= 
will come out in ft, as shown in
Example B.
= 4.18 ´ 109 
in. = 1.56 ´ 10–2
ft
