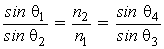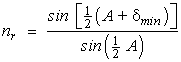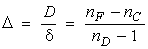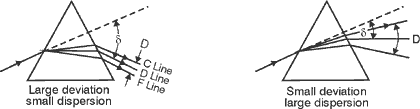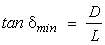|
MODULE 6–7 PRISMS General Comments of Leno Pedrotti © Copyright 1987 by The Center for Occupational Research and Development All rights reserved. No part of this book may be reproduced in any form or by any means without permission in writing from the publisher. The Center for Occupational Research
and Development Printed in the U.S.A. ISBN 1-55502-024-0 (1) A prism is a solid, transparent object that has polished, plane surfaces. The surfaces generally are tilted with respect to one another. It is used to refract and/or reflect light. (2) Many forms and shapes of prisms are used singly or in combination in optical instruments. They may be completely transparent, or may have one or more surfaces silvered for high reflection to prevent loss of light through transmission. They may be used to displace the path of light around obstacles or to invert, reverse or rotate images. Prisms also may be used to separate light into its component frequencies or polarizations. In other words, they may be used for reflection, refraction, chromatic dispersion, polarization or some combination of these. (3) This module will acquaint you with functional classes of prisms. It also describes specific configurations and applications of several commonly used prisms.
DISCUSSION (4) A prism is used to change the path of part or all of a beam of light that is transmitted through it. Prisms can be classified into the following categories according to their use.
(5) The following discussion will be divided into these classifications of prisms. We will give examples of instruments in which the prisms are used.
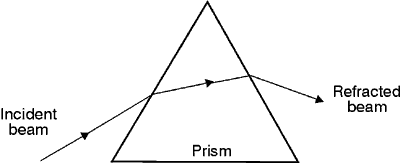
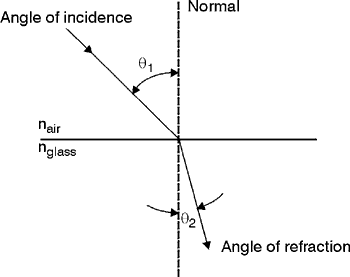
Prisms to Deviate Light by Refraction (6) Figure 1 is a simple sketch of a prism used to deviate light by refraction. Refraction is a change in the direction of light rays as they pass from one material to another, across a well-defined surface or interface. Fig. 1 (7) When you studied refraction, you learned that there’s a relationship between the angle of incidence, angle of refraction, and the indices of refraction of the materials. This relation—known as Snell’s law—is shown in Figure 2. The angle of incidence q1 and the angle of refraction q2 are measured between the light rays and the normal to the surface. The relationship between the angle of incidence and the angle of refraction is given by Snell’s law as Fig. 2
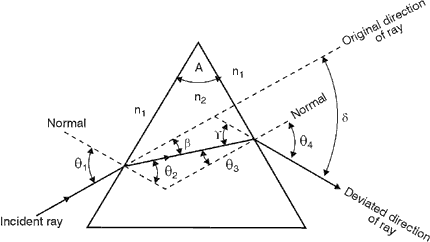
(8) Refraction by a prism usually involves a light ray passing from air into glass and from glass into air. In a prism, the entrance and exit plane surfaces are inclined at some angle (called the apex angle) so that the deviation produced by the first is not canceled by the second but is further increased. The path of a light ray refracted through a prism according to Snell’s law is traced in Figure 3. (9) Refraction of the ray at the two surfaces obeys Snell’s law, so that in terms of the angle shown
(10) The incident ray is deviated an amount b by the first surface and an amount g by the second surface. The total angle of deviation d between the incident and emergent rays is the sum of the deviation angles at each surface.
Fig. 3
(11) With the help of trigonometry, we also can express the deviation angle of a prism, d, in terms of the incident angle, q1, the emergent angle, q4, and the apex angle A of the prism.
(12) The index of refraction (n2) that occurs in Snell’s law is not the same for all wavelengths of light. For most transparent materials, the index increases slightly as the wavelength decreases, that is, it’s slightly greater for violet light than for red light. As a result of this difference in refractive index, rays of violet light incident on a prism at a given angle are bent more sharply than are rays of red light incident at the same angle. Table 1 shows the index of refraction of borosilicate crown glass (a typical prism material) for selected wavelengths in the visible spectrum. Table 1. Index
of Refraction for Borosilicate Crown
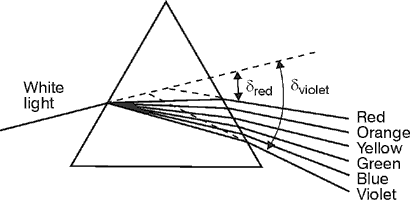
(13) You can see in Figure 4 that the total angle of deviation for red light (dred) is less than the total angle of deviation for violet light (dviolet). The difference in these deviation angles (dviolet – dred) is a measure of how well the prism disperses white light. Fig. 4
Prisms Used
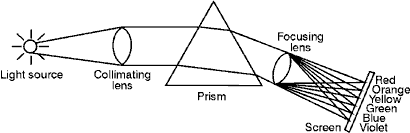
to Disperse Light into (14) This phenomenon—known as dispersion—can be either an advantage or a disadvantage of prisms depending upon their application. For example, an equilateral prism such as in Figure 4 can be effectively used for chromatic dispersion in a spectrograph. A spectrograph uses collimated light transmitted through a prism arrangement as shown in Figure 5. The composite light beam then is focused to a line image having the red components on one end of the line and the violet components on the other end. The dispersion is too great in the equilateral prism, however, for that prism to be used when forming an image. Fig. 5
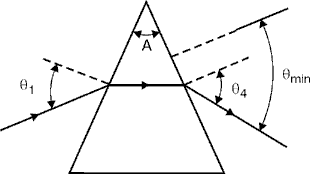
Minimum Deviation Angle of a Prism (15) For a symmetrical prism (one in which the apex angle lies at the top of an isosceles triangle), the total deviation angle d of the light is minimized when the light ray inside the prism travels parallel to the prism’s base. (See Figure 6.) Note that q1 = q4 and the ray inside the prism is parallel to the base. Fig. 6 (16) More advanced books on optics show that you can calculate the relative index of refraction of the prism if you measure the minimum deviation angle. (17) Equation 5 gives us an accurate way to determine the index of refraction of an unknown prism material if the minimum deviation angle is carefully measured.
where: nr = nglass / nsurroundings
The Dispersive Power of a Prism (18) The dispersive power of a prism is a measure of how well the device separates light into its component wavelengths. Dispersive power D is defined mathematically as the ratio of the angular dispersion D of light exiting the prism to the total deviation angle d.
(19) The relationship between D and d is shown in Figure 7. Note that a prism with high deviation does not necessarily have good dispersion. Fig. 7 (20) The reciprocal of the dispersive power is D defined as the Abbe Number. As you can see readily in Figure 7, the larger the dispersive power D, the larger is the spread D of the two reference lines (C and F) and the smaller is the deviation angle d of the standard line (D) from the original ray direction. If instead one uses the Abbe Number to describe the dispersive character of a prism, the larger the Abbe Number, the larger is the overall deviation angle d compared to the dispersion D of the reference C and F lines. (21) For the left diagram of Figure 7, the prism shown has a lower dispersive power D and a higher Abbe Number, while in the right diagram, the prism shown has a higher dispersive power D and a lower Abbe Number. (22) Wavelengths that are traditionally used in the definition of dispersion of optical glass come from the so-called Fraunhofer lines. These three wavelengths, designated F, C, and D, were among the lines studied by J. von Fraunhofer in the solar spectrum. They are convenient because the lines F and C lie at either end of the visible spectrum while D lines lie near the middle. The F and C lines originate from atomic hydrogen. The D line originates from atomic sodium. Table 2 gives the wavelength of the F, C, and D lines as well as the index of refraction of crown and flint glass at those wavelengths. Table 2. Index
of Refraction of Crown and Flint Glass
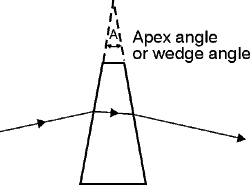
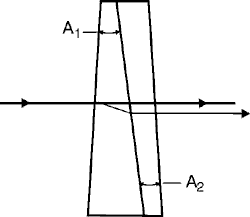
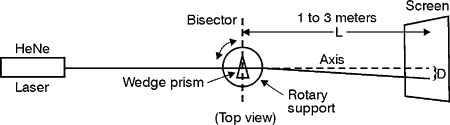
(23) A wedge prism, as shown in Figure 8, is a prism with a very small apex angle. Wedges are often truncated prisms. They are specified according to either the wedge angle (apex angle of prism) or the refracting angle for light entering perpendicular to one face. You can use a wedge prism to form an image if the image being formed is not greatly magnified. A small amount of dispersion often can be corrected by using a compound wedge prism made up of two wedges with different indices of refraction, placed together with opposite orientations as shown in Figure 9. Wedges can be rotated about an axis perpendicular to the entrance face to scan a transmitted light ray in a conical locus as in search radar. Fig. 8
Fig. 9
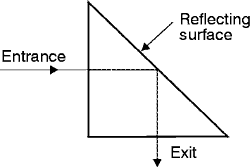
Prisms Used to Deviate a Light Path by Reflection (24) Figure 10 shows a prism used to deviate a light path by reflection. In this type of prism, one or more of the plane surfaces acts as a mirror(s). Reflection from these surfaces can be achieved in either of two ways: Fig. 10
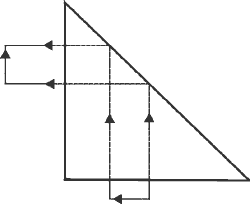
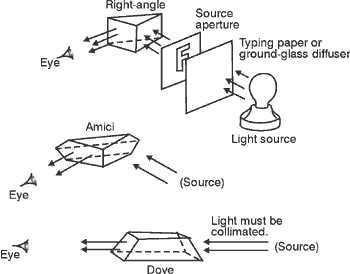
(25) Right-angle prisms as shown in Figure 11 are basic prisms that can be used in several different applications. (26) The Porro prism is a right-angle prism in which the light enters through the face opposite the right angle. The light then is reflected twice by total internal reflection from the opposite faces. Then it exits from the same face through which it entered. It’s used often as a rotating reflector, Q-switch in lasers. See a Porro prism in Figure 12. Fig. 11
Fig. 12 (27) Notice that a Porro prism reverses an image in the plane in which the reflection takes place. When two Porro prisms are placed at right angles to each other and in such a way that the light exiting the first prism will enter the second, the image is rotated and reversed as you can see in Figure 13.
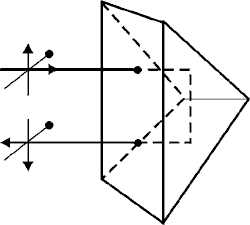
Fig. 13 (28) This particular combination of Porro prisms is used commonly in binoculars. The image formed by the objective lens is reversed. But after the light passes through the Porro prisms, it will be reverted and will have the same orientation as the original object seen by the observer. (29) The Dove prism, as shown in Figure 14, is a special case of a 45° – 90° – 45° prism with the triangle truncated. The Dove prism interchanges the two rays. If the prism is rotated about the direction of the light, the rays rotate around each other at twice the angular velocity of the prism. This is shown in Figure 15. This rotation feature makes a Dove prism usable in the viewfinder of a camera. Any slight change in the camera’s horizontal position will be exaggerated by the prism and allow the operator to correct for it.
Fig. 14
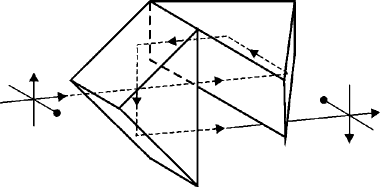
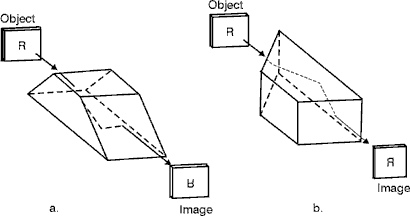
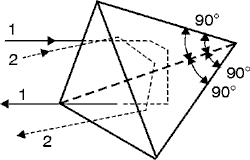
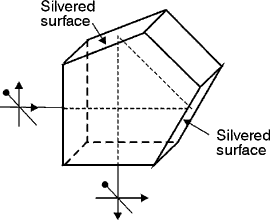
Fig. 15 (30) The Amici prism is a right-angle prism that usually has a 90° roof on the face opposite the right angle. Figure 16 shows such a prism. The fact that these prisms often have inverting roofs results in their being called roof prisms. However, many other prisms can be fitted with roofs. The purpose of the roof is to invert the image left to right. If the two reflecting surfaces of the roof don’t intersect within a few seconds of 90°, the beams reflected from them will not match and a double image will be formed. Fig. 16 (31) Amici prisms often are used in simple direct-vision spectrographs and in sighting equipment for the military. (32) The cube corner reflector uses three mutually orthogonal, reflective surfaces. It redirects a beam through 180° regardless of incident angle to the prism. The cube corner reflector is used as a passive cooperative target for laser radars, range measurement, and angle-tracking systems. (See Figure 17.) Fig. 17 (33) A Penta prism, as shown in Figure 18, has five sides with one angle equal to 90°. Fig. 18 (34) This prism deviates the beams exactly 90° in the principal plane even if the beam doesn’t strike the end faces exactly normal. Both reflecting surfaces must be silvered because the angle of incidence is not large enough to permit total internal reflection. (35) High-precision rangefinders use Penta prisms. The angles measured by these rangefinders are so small that, if such prisms were not used, the normal bending of the tube of the instrument would produce large errors. Penta prisms minimize the bending effect. (36) When you merely want to displace the axis of a beam without introducing deviation and without reverting or inverting the image, you can use a rhomboidal prism. (See Figure 19.) They often are applied in eyepieces where we need to provide a way to adjust to various observers. Fig. 19
Prisms Used
to Separate Polarization (38) A beam of ordinary (unpolarized) light is composed of random, transverse vibrations of the electric field. Each vibration is caused by one of many different atoms in the light source. (39) The amplitudes of each of the many random transverse vibrations can be divided into components along two orthogonal axes, each perpendicular to the direction of propagation. This is called "dividing" the light into two polarized components. (40) It’s enough for this module for you to know that certain prisms can be used to separate the two perpendicular polarization components of a light beam. These prisms are made of an optical material that has a characteristic called "birefringence" or "double refraction." Birefringence in an optical material means that the material behaves as if it has a different index of refraction for one polarized component of a light beam than for the other polarized component. If the material is made into a prism, it will refract or bend one polarized component of a light beam more than the other polarized component, since the angle of refraction, in Snell’s law, depends on the indices of refraction. As a result of this, a single, ordinary beam will enter a polarizing prism and two polarized beams will emerge, either displaced and traveling parallel or traveling in slightly different directions. (41) The two rays that emerge are called the "O-ray" or ordinary ray, and the "E-ray" or extraordinary ray. Only the ordinary ray follows the path predicted by using Snell’s law. (42) The optical materials in which the phenomenon of double refraction is observed are crystalline quartz and calcite. Calcite is used more frequently because the separation of the two polarization components is greater. Calcite (calcium carbonate) has a crystal structure that causes it to form easily or cleave easily into a rhombohedral shape (as shown in Figure 20). Each face of the crystal is a parallelogram whose angles are 71° and 109º. Figure 20 shows the double refraction of light in a calcite prism. Both the E- and O-rays are shown, with the E-ray emerging above the O-ray. Fig. 20 (43) Figure 21 shows a Nicol prism, also made of calcite. In the Nicol prism, the calcite rhombohedron is precisely cut into two halves. Then it’s polished and cemented back together with Canada balsam. Because of its geometry, and the relative indices of refraction of calcite and Canada balsam, the Nicol prism will remove one of the two refracted rays by total reflection. The Nicol prism is therefore used as a polarizer or analyzer. Fig. 21 (44) We often want to split a light beam into two linearly polarized components that leave the prism in different directions. This is accomplished in a Wollaston prism, made from two pieces of crystalline quartz. The two pieces are cut from different crystal orientations and cemented together with glycerine or castor oil. See Figure 22. A Wollaston prism also can be used to combine two light beams of different polarization. The arrangement would be the same as that shown in Figure 21, but the arrows on the light rays now would be reversed. Fig. 22 (45) Prism polarizers are much more effective at polarizing light than are inexpensive sheets of Polaroid Hi lm. A common test of a polarizer’s effectiveness is the so-called "extinction ratio" (ER). As defined in Equation 7, the ER for a pair of polarizers is the ratio of the maximum light transmitted by a pair of polarizers, divided by the minimum power transmitted.
(46) Inexpensive polarizing sheets (such as Polaroid H, K or HR types) often have extinction ratios of 300 to 500. Prism polarizers can have ERs of 106 or more, but cost about one hundred times as much as the sheet-type polarizers. The inexpensive sheet polarizers work on selective absorption of light while the prism polarizers work on refraction and, often, reflection. So the prism polarizers are much less prone to damage from intense light, such as is present in a typical laser beam. (47) Exercises 1 through 8 consist of identifying the eight prisms shown. In the space provided by each drawing, explain the important characteristics of that prism, as outlined in the text.
Wedge prism Right-angle prism Amici prism Dove prism 1-mW HeNe laser One-meter optical benches (two) Incandescent light source Prism holder with capability for rotating prism about horizontal axis Lens holders (two) Ground glass screen Screen holder Rotation table component support "F-shaped" source aperture Lenses, positive, 6-inch focal length, 2-inch diameter (two) 1-inch-diameter stop
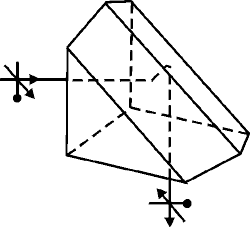
Hecht, E. Optics, 2nd edition. Addison-Wesley, 1987. Jacobs, Donald H. Fundamentals of Optical Engineering. New York: McGraw-Hill Book Company, Inc., 1943. Jenkins, F. A., and H. E. White. Fundamentals of Optics, 4th edition. New York: McGraw-Hill Book Company, Inc., 1976. Kingslake, Rudolf. Applied Optics and Optical Engineering, Vol. 3. New York: Academic Press, 1965. Mauro, J. A. Optical Engineering Handbook. Syracuse, NY: General Electric Company, 1966. Optics Guide 3. Melles Griot, 1770 Kettering Street, Irvine, CA 92714, (714) 261-5600. Pedrotti, Frank L., and Leno S. Pedrotti. Introduction to Optics, Chapter 3. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1987. Shortley, G., and D. Williams. Elements of Physics. Englewood Cliffs, NJ: Prentice-Hall, 1955 SPIE. Basic Optics and Optical Instruments, Vol. 1. Redondo Beach, CA: Northrop Corporation, 1965.
|